Calculatrice de dérivées

Cette calculatrice de dérivée vous guidera à travers toutes les étapes et les règles utilisées pour trouver la dérivée d'une fonction donnée. Vous devez taper une fonction comme 3x + sin(x^2), ou vous pouvez la faire précéder de la définition complète de la fonction, comme f(x) = 3x^ 2 + 2tan(x^3).

Notez que l'on peut parler de calculatrice de dérivée première comme d'une calculatrice de dérivée. La dérivée première et la dérivée représentent la même chose, et la partie "première" est généralement supprimée.

La fonction fournie peut être entièrement simplifiée ou non, cela n'a pas d'importance, car la calculatrice simplifiera d'abord la fonction si nécessaire avant de calculer sa dérivée.

Une fois qu'un fonction valide a été fournie, il vous suffit de cliquer sur "Calculer", d'attendre quelques secondes, et toutes les étapes du calcul vous seront présentées.

La différenciation est le principal outil utilisé en calcul (avec l'intégration) et c'est une opération cruciale qui est largement utilisée dans les mathématiques plus avancées. Parmi les applications les plus courantes, on peut citer tangent line calculation , les maxima et les minima et bien d'autres choses encore.

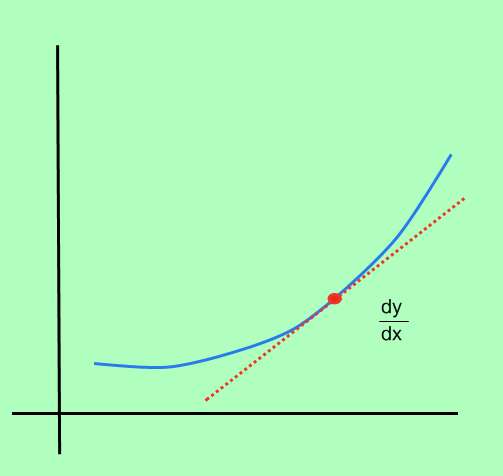
Comment calculer la dérivée d'une fonction ?

Le processus de calcul de la dérivée d'une fonction est appelé différenciation et elle consiste à déterminer le taux de variation instantané du point, en tout point du domaine de la fonction.

Qu'est-ce que le taux de variation instantané d'une fonction ? Eh bien, commençons par la définition de taux de changement : Considérons une fonction \(f\), et supposons que nous avons deux points, \(x_0\) et \(x_1\). Au point \(x_0\), la fonction est \(f(x_0)\), et au point \(x_1\), la fonction prend la valeur \(f(x_1)\)

La variation de f est alors définie comme \(\Delta y = f(x_1) - f(x_0)\) (qui est également appelée variation de y). De même, la variation de x est définie comme \(\Delta x = x_1 - x_0)\). En d'autres termes, \(\Delta x\) est la variation de x, tandis que \(\Delta y\) est la variation de la valeur de la fonction, due à la variation de x.

Graphiquement :

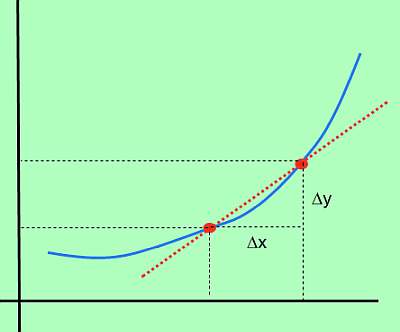
Formule dérivée

Ainsi, si \(\Delta x\) représente la variation de x, et\(\Delta y\) représente la variation de la valeur de la fonction, due à la variation de x, les valeurs correspondantes taux de changement est :

\[\text{Rate of Change} = \displaystyle \frac{\Delta y}{\Delta x} \]

Dans ce cas, quel serait le taux de changement instantané ? Cela correspondrait à l'analyse de ce qui se passerait si \(\Delta x\) devenait vraiment petit. On pourrait s'attendre à ce que \(\Delta y\) devienne également petit, mais qu'adviendrait-il du taux entre \(\Delta y\) et \(\Delta x\) ?

Ainsi, dans ce contexte, le taux de changement instantané est défini comme suit

\[\text{Instant Rate of Change} = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} \]

Ainsi, en termes simples, nous fixons \(x_0\) et nous calculons le taux de changement pour des valeurs de \(x_1\) de plus en plus proches de \(x_0\). En utilisant cette idée de taux de changement instantané, nous pouvons donner la formule suivante pour la dérivée en un point \(x_0\).

\[f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \]

Si la limite ci-dessus existe, on dit que la fonction f est différentiable sur \(x_0\). Nous dirons également qu'une fonction est différentiable sur un ensemble A, si la fonction est différentiable en tout point de l'ensemble.

Étapes de l'utilisation de la formule de dérivation

• Étape 1 : Identifiez clairement la fonction f que vous voulez différencier
• Étape 2 : Veillez à simplifier f autant que possible, sinon la recherche de la limite requise risque d'être inutilement difficile
• Étape 3 : Décidez si vous allez travailler avec un point générique x0, ou si vous donnez un point numérique spécifique pour x0
• Étape 4 : Sur la base de la définition de la fonction, utilisez la formule \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \). Il s'agit d'introduire les valeurs de x0 et x1 dans f, et de voir comment la formule se présente algébriquement
• Étape 5 : Simplifiez autant que vous le pouvez AVANT de prendre la limite
• Étape 6 : Parfois, il est plus facile de définir x1 = x0 + h, puis de calculer la limite lorsque h converge vers 0

Remarquez que l'étape 6 est celle que certains considèrent comme la formule par défaut. En effet, la formule de dérivation alternative qui peut sembler plus facile à des fins de simplification est la suivante :

\[f'(x_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \]

qui est la formule que vous trouverez peut-être dans votre manuel, au lieu de l'autre.

Règles relatives aux produits dérivés

Le calcul de la dérivée à l'aide de la formule semble représenter un travail considérable. Et en effet, cela pourrait être un processus laborieux si nous décidions d'effectuer chaque processus de différenciation à l'aide de la formule de la dérivée.

Heureusement, il existe un certain nombre de fonctions (à savoir polynômes , fonctions trigonométriques ) dont on sait avec précision quels sont leurs dérivés.

En plus de cela, nous avons règles de différenciation qui nous permettent de trouver la dérivée d'une fonction qui est un Fonction composite et/ou une combinaison de fonctions élémentaires (dont on connaît la dérivée), en termes de dérivées élémentaires.

Quelles sont les étapes du calcul de la dérivée ?

• Étape 1 : Identifiez la fonction f que vous voulez différencier. Simplifiez autant que vous le pouvez AVANT de calculer sa dérivée
• Étape 2 : Déterminez si vous êtes tenu d'utiliser la formule de dérivation ou non
• Étape 3 : Si vous devez utiliser la formule de la dérivée, utilisez \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \), ou vous pouvez utiliser \(f'(x_0) = \displaystyle \lim_{h \to 0}\frac{f(x_0+h) - f(x_0)}{h} \) si cela vous semble plus facile à aborder
• Étape 4 : Si vous n'êtes pas obligé d'utiliser la formule de dérivation, vous pouvez utiliser les principales règles de différenciation : La linéarité, Règle Du Produit , Quotient Rule et Règle De La Chaîne qui vous aidera à réduire le calcul de la dérivée à l'utilisation de dérivées de base connues

Souvent, la fonction que vous essayez de trouver la dérivée pour n'est pas une fonction simple, mais c'est une combinaison de base de plusieurs fonctions simples. Par exemple, la fonction

\[f(x) = x + \cos(x) + \sin(x)\]

n'est pas une fonction élémentaire en soi, mais elle est Fonction composite de trois fonctions élémentaires, \(x\), \(\sin x\) et \(\cos x\).

Applications des produits dérivés

On pourrait penser que "les dérivées impliquent des limites et que c'est super théorique, alors elles ne doivent pas avoir beaucoup d'applications", mais on aurait tout faux. La magie des dérivées est qu'elles concernent essentiellement le taux de changement des fonctions, qui peuvent représenter différents types de processus.

C'est pourquoi la différenciation permet d'étudier le processus de changement, et de comparer des variables changeantes, ce qui a une large applicabilité.

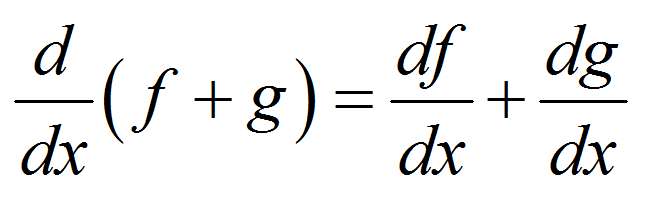
Exemple : calcul de la dérivée

Calculer la dérivée par rapport à x pour \(f(x) = \displaystyle \frac{x}{3} + \frac{5}{4} \cos(x) - \frac{5}{4} \sin(x^2)\)

Solution : La fonction suivante a été fournie : \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\), pour laquelle nous devons calculer sa dérivée.

Étape Initiale : Dans ce cas, nous devons d'abord simplifier la fonction \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right) \), et pour ce faire, nous procédons aux étapes de simplification suivantes :

Après avoir simplifié la fonction, nous pouvons procéder au calcul de la dérivée :

Le graphique suivant est obtenu pour \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\) sur l'intervalle \([-5, 5]\) :

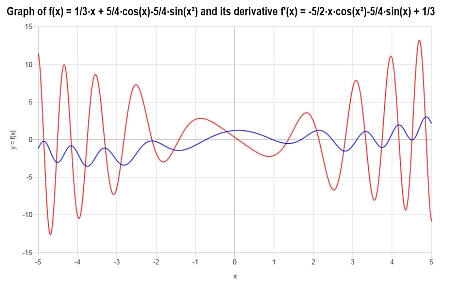
Exemple : différenciation d'une fonction

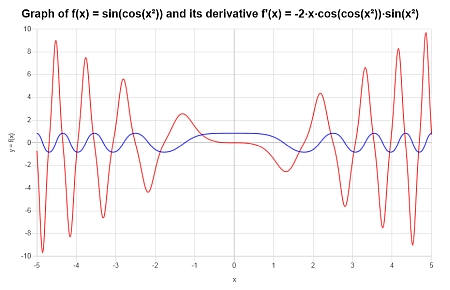
Calculer la dérivée de : \(f(x) = \sin(\cos(x^2))\), et donnez le graphique de \(f(x)\) et \(f'(x)\).

Solution : Nous avons maintenant \(\displaystyle f(x)=\sin\left(\cos\left(x^2\right)\right)\).

La fonction est déjà simplifiée, nous pouvons donc calculer directement sa dérivée. En utilisant cette dérivée, nous obtenons

Par conséquent, nous obtenons le graphique suivant pour la fonction sur l'intervalle \([-5, 5]\) :

Exemple : calculatrice de dérivée

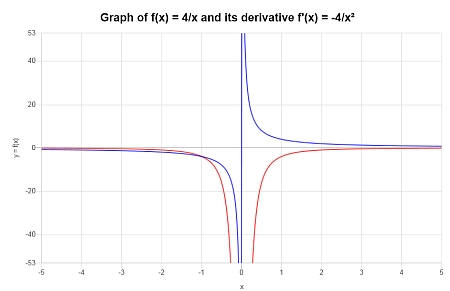
Trouvez la dérivée de \( f(x) = \displaystyle \frac{4}{x}\). Est-elle bien définie partout ? Représentez-la graphiquement.

Solution : La fonction fournie pour laquelle le dérivé est nécessaire est \(\displaystyle f(x)=\frac{4}{x}\).

Aucune autre simplification n'est nécessaire, nous pouvons donc procéder directement au calcul de sa dérivée :

Graphiquement :

En savoir plus sur les dérivés et les fonctions

Le Présent calculatrice de dérivées avec étapes vous sera très utile puisqu'il effectuera le calcul de la dérivée d'une fonction donnée, en montrant toutes les étapes du processus, en appliquant la méthode de calcul des Règles relatives aux produits dérivés il s'agit d'un outil qui vous permet de savoir à quel moment et pour quelle raison ils sont appliqués.

Ce calculateur peut également être appelé calculatrice dy dx ou calculatrice de quotient différentiel car c'est précisément ce qu'il fait, il calcule la limite du rapport dy/dx lorsque dx se rapproche de 0.

Les fonctions sont des concepts extrêmement importants en mathématiques. Outre la différenciation, vous devez être capable de simplifier une fonction généralement, comme préambule à d'autres calculs plus spécialisés. Il existe des types spéciaux de fonctions qui vous permettent d'effectuer des opérations spécifiques, comme ce que vous faites avec Opérations polynomiales .

Il est intéressant de noter que de nombreux éléments importants, comme la recherche des coordonnées de la sommet d'une parabole qui peut être dérivé de manière astucieuse en utilisant des arguments géométriques, peut être obtenu de manière triviale en utilisant la différenciation.

De même, l'idée de Ligne Tangent et Approximation Du Premier Ordre apparaissent naturellement, découlant du concept de dérivé, et d'une extension naturelle.