Aprende más sobre esta calculadora de intersección y con pasos.

La intersección y de una recta es el punto en el que la recta cruza el eje $y$, y es un punto muy relevante en muchos contextos.

Para utilizar esta calculadora tienes que seguir los siguientes pasos:

1. Seleccione una forma de definir la línea. En realidad, puede proporcionar una ecuación de la línea , proporcione dos puntos de la recta, o un punto de la recta y la pendiente
2. Asegúrese de elegir al menos uno de los métodos y proporcione la información requerida para la opción seleccionada
3. Haga clic en "Calcular"

¿cómo se calcula la intersección y?

La forma de calcular la intersección y dependerá de cómo se haya especificado la recta. A menudo, se puede observar la gráfica de la línea y estimar más o menos dónde cruza el eje y, que es la encontrar la intersección y en el método de la gráfica .

De este modo, podrás hacerte una idea al menos del valor aproximado de la intersección y

¿cómo se encuentra la intersección y con la pendiente?

Lo ideal, sin embargo, es calcular la intersección y algebraicamente. Por ejemplo, cuando se tiene la ecuación en forma de pendiente e intercepción, utilizando la fórmula de la línea.

$$y = mx + n$$

ya sabes que la intersección y es $n$. ¿Por qué? Porque $y$, en función de $x$ es $y = mx + n$. Entonces, cuando x = 0, obtenemos $y = n$, y sabemos que $x = 0$ es el punto donde la gráfica cruza el eje y

¿la intersección y es un número o un par (x, y)?

Depende un poco de la convención que se utilice. Si el valor y en el que la línea cruza el eje y es $y_{intercept}$, entonces la forma más utilizada es que la intersección y sea el par $(0, y_{intercept})$.

Aunque, si dices que la intersección y es simplemente $y_{intercept}$, también es correcto, sólo que algunos instructores te pedirán que escribas la intersección y como un par ordenado.

Pero la coordenada x de la intersección y es SIEMPRE 0, por lo que algunas personas consideran redundante escribir el par completo.

¿puedo obtener la calculadora de la intersección y a partir de dos puntos?

Sí. En ese caso, es necesario utilizar primero el dos puntos para encontrar la pendiente utilizando la siguiente fórmula

$$m = \frac{y_2 - y_1}{x_2 - x_1}$$

Una vez que tengas la pendiente, puedes construir la forma punto-pendiente usando

$$y - y_1= m (x -x_1)$$

Y luego resolviendo para $y$ se obtendrá el forma de intersección de pendientes , que te da la intersección y directamente

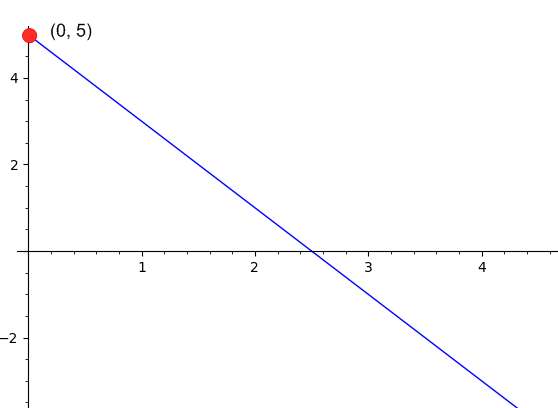
Ejemplo: cálculo de la intersección y dadas dos rectas

Sabes que una recta pasa por los puntos $\left(\displaystyle \frac{1}{4}, 1\right)$ y $\left(\displaystyle \frac{15}{2}, 6\right)$. Encuentra la intersección en y de la recta.

Solución: : Cálculo de la intersección y de la recta

La información proporcionada sobre la recta es que ésta pasa por los puntos$\displaystyle \left( \frac{1}{4}, 1\right)$ y $\displaystyle \left( \frac{15}{2}, 6\right)$

Por lo tanto, el primer paso consiste en calcular la pendiente. La fórmula de la pendiente es $$\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1}$$

Ahora, enchufando los números correspondientes es , obtenemos que la pendiente es: $$\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle 6 - 1}{ \displaystyle \frac{15}{2} - \frac{1}{4}} = \frac{ \displaystyle 6-1}{ \displaystyle \frac{15}{2}-\frac{1}{4}} = \frac{20}{29}$$

Entonces, ahora sabemos que la pendiente es $\displaystyle m = \frac{20}{29}$ y que la recta pasa por el punto $\displaystyle \left( \frac{1}{4}, 1\right)$

Por lo tanto, con la información que tenemos, podemos construir directamente la forma punto-pendiente de la línea, que es

$$\displaystyle y - y_1 = b \left(x - x_1\right)$$

y, a continuación, insertando los valores conocidos de $\displaystyle b = \frac{20}{29}$ y $\displaystyle \left( x_1, y_1 \right) = \left( \frac{1}{4}, 1\right)$, obtenemos que

$$\displaystyle y-1 = \frac{20}{29} \left(x-\frac{1}{4}\right)$$

Ahora, tenemos que expandir el lado derecho de la ecuación distribuyendo la pendiente, por lo que obtenemos $$\displaystyle y = \frac{20}{29} x + \frac{20}{29} \left(-\frac{1}{4}\right) + 1$$

y simplificando obtenemos que $$\displaystyle y=\frac{20}{29}x+\frac{24}{29}$$

Conclusión : A partir de los datos proporcionados, concluimos que la recta cruza el eje y en $\displaystyle y = \frac{24}{29}$, por lo que el punto de intersección y correspondiente es $\displaystyle \left(0, \frac{24}{29}\right)$.

Otro cálculo que puede interesarle también es el que utiliza nuestro calculadora de intersección x que es el punto donde la línea cruza el eje x.

Los interceptos de una línea proporcionan una excelente intuición gráfica de lo que hace la línea, y tienen aplicaciones directas cuando resolución de sistemas de ecuaciones o en economía cuando se calculan los excedentes de los consumidores y productores.