Mehr zu diesem linearen gleichungsgrafiker

Grafiklinien sind grundlegende Fähigkeiten und dieser Taschenrechner hilft Ihnen dabei.Sie müssen zunächst die bereitstellen Lineare Gleisung Sie möchten sich drapieren.

Sie können jede lineare Gleichung explizit bereitstellen, z. B. x + 3y = 2 oder etwas, das nicht vollständig vereinfacht ist wie x + 3y = 2/3 x.

Grafiklinien hat so viele Anwendungen, dass es zu einer sehr praktischen Fähigkeit wird, zu erwerben.Geometrisch haben Linien eine sehr einfache Intuition, die es einfach macht, sich zu grafieren, da wir nicht viele Informationen benötigen, um sie anzugeben.

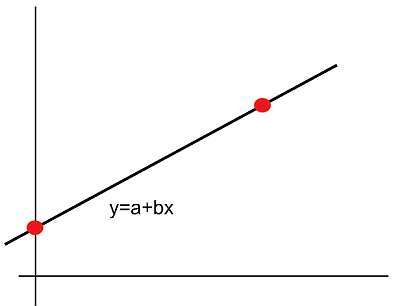
Wie grafikiere ich lineare gleichungen?

Sie können dies verwenden Grafikrechtner Zeilen grafisch.Wenn Sie es manuell tun, müssen Sie sich bewusst sein, dass der Ansatz eine Präambel erfordert, die von der Art der bereitgestellten Informationen abhängt.

Was sind die schritte zum grafieren einer linie?

• Schritt 1: Identifizieren Sie die Art der bereitgestellten Informationen.Haben Sie eine tatsächliche Gleichung vorgesehen, haben Sie zwei Punkte, einen Punkt und die Steigung, die Steigung und den Y-Schnur?Eindeutig beurteilen
• Schritt 2: Unabhängig von den angegebenen Informationen finden Sie zwei Punkte, an denen die Linie durchgeht.Lösen Sie beispielsweise für y für y für x = 0 und x = 1 zum Beispiel.Für Steigung und Y-Abschnitt konstruieren Sie die Gleichung y = a + bx und finden Sie zwei Punkte.Wenn Sie einen Punkt und eine Steigung haben, definieren Sie y = y1 + b (x-x1) und schließen Sie ihn bei x = 0 an
• Schritt 3: Sobald Sie zwei Punkte haben, an denen die Linie durchgeht, verfolgen Sie einen Lineal, um eine Linie zu verfolgen, die durch sie verläuft

Linien sind super einfach zu zeichnen, nur Sie müssen methodisch sein und sich der Art der verfügbaren Informationen bewusst sein.

Selbst wenn Sie es von Hand tun, ist es immer schön, einen handlichen Linear zu haben Graphing Calculator online um Ihre Ergebnisse zu überprüfen.

Grafiklinien

Grafiklinien haben so viele Anwendungen.Zum Beispiel können Sie Lösen Sie Ein Gleichungssystem durch Grafik der entsprechenden Linien und sehen, wo sie sich schneiden.

Wenn die Linien parallel sind und sich nicht überschneiden, gibt es keine Lösungen.

Ähnlich wie bei Addition und Subtraktion wird die Trennung von Fraktionen nur aus der Multiplikation von Fraktionen abgeleitet: Um zwei Brüche zu teilen, multiplizieren Sie sich nur zuerst mit dem Umgekehrter Bruch des zweiten (die inverse Fraktion wird durch Tausch des Zählers durch den Nenner in der Fraktion erhalten).

Andere anwendungen linearer graphen

Linien oder Lineare Graphen sind überall wirklich präsent. Lineare Funktionen erscheinen ständig in Anwendungen, in Kalkül und Optimierung, sodass sie wirklich nützlich sind.

Beispiel: beispiel für lineargleichungsgrafikern

Grafik die folgenden Gleichungen: \(\frac{1}{2}x + \frac{7}{4}y = 0\)

Lösung: Wir müssen mit der folgenden Gleichung arbeiten:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Zuerst mit den Konstanten arbeiten:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Das Ergebnis wird erhalten, indem (y) auf der linken Seite und (x) und die Konstante auf der rechten Seite platziert wird:

\[\displaystyle \frac{7}{4}y = -\frac{1}{2}x \]

Dann wird der Prozess fortgesetzt, indem für \(y\) gelöst wird und dann beide Seiten der Gleichung durch \(\frac{7}{4}\) geteilt werden.Wir bekommen dann:

\[\displaystyle y=-\frac{\frac{1}{2}}{\frac{7}{4}}x\]

Und nach der Vereinfachung ist das Ergebnis wie folgt.

\[\displaystyle y=-\frac{2}{7}x\]

Fazit : Wir schließen darum, dass die Gleichung der Linie in Steigabschnittform, die auf den verfügbaren Daten basiert, \(\displaystyle y=-\frac{2}{7}x\) mit einer Steigung von \(\displaystyle b = -\frac{2}{7}\) und y-Schnittstelle von \(\displaystyle n = 0\) ist.

Daher ist die Grafik der bereitgestellten Linie

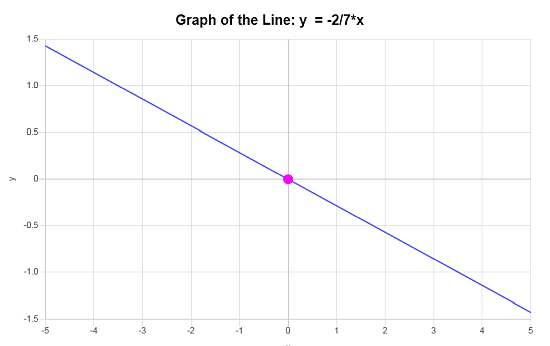
Beispiel: beispiel für lineargleichungsgrafikern

Holen Sie sich die Zeile, die darstellt: \(\frac{2}{3}x + \frac{5}{4}y = - \frac{5}{6}x + 2\)

Lösung: Wir wurden mit der folgenden Gleichung versehen:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Arbeiten mit den Konstanten:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Nun, put \(y\) auf der linken Seite und \(x\) und die Konstante auf der rechten Seite bekommen wir

\[\displaystyle \frac{5}{4}y = \left(\frac{-5}{6}-\frac{2}{3}\right)x +2\]

Jetzt ist der Begriff \(y\) \( \frac{5}{4} - 0 = \frac{5}{4}\) und auch da \( -\frac{5}{6} - \frac{2}{3} = -\frac{3}{2}\) wird Folgendes erhalten

\[\displaystyle \frac{5}{4}y=-\frac{3}{2}x+2\]

Wenn Sie nun für \(y\) gelöst werden, indem beide Seiten der Gleichung durch \(\frac{5}{4}\) geteilt werden, wird Folgendes erhalten

\[\displaystyle y=-\frac{\frac{3}{2}}{\frac{5}{4}}x+\frac{2}{\frac{5}{4}}\]

und vereinfachen wir endlich die folgenden

\[\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\]

Fazit : Basierend auf den bereitgestellten Daten schließen wir, dass die Gleichung der Linie im Steigungsschnittschnitt \(\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\) mit einer Steigung von \(\displaystyle b = -\frac{6}{5}\) und y-Schnittstelle von \(\displaystyle n = \frac{8}{5}\) ist.

Das lineare Diagramm ist

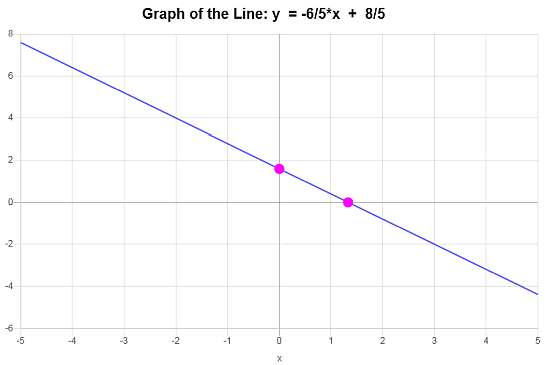
Weitere zeilenrechner

Zeilen sind so wichtig, dass sie ihren eigenen Abschnitt im Buch der Mathematik verdienen.Sie können berechnen Lineare Gleiungen in verschiedenen Formen je nach spezifischer Bedürfnisse.

Die Bestimmung von Linien benötigen letztendlich Zwei Punkte, ein Denen Die Linie Durchläft , die direkt oder indirekt angegeben werden können.