Ce calculateur de formule de vertex

Ce calculateur permettra d'appliquer le formule des sommets pour une fonction quadratique donnée que vous fournissez. Cette fonction quadratique doit être une fonction valide telle que 2x^2 + 3x + 1/3, ou elle peut venir non simplifiée telle que 2x^2 - x + 5 - 3/4 x^2 +1/3, etc. Toute fonction quadratique valide fera l'affaire.

Une fois que vous avez fourni une fonction quadratique valide, vous devez cliquer sur le bouton "Calculer", et les étapes de l'application de la formule du sommet seront affichées, avec les étapes suivies pour calculer le sommet de la parabole.

Les fonctions quadratiques sont vraiment importantes dans les applications d'algèbre et de calcul, et le sommet d'une fonction quadratique est très interprétable.

Quelle est la formule du sommet ?

Tout d'abord, nous supposons que nous partons d'une fonction quadratique, et que nous l'avons simplifiée :

\[ f(x) = ax^2 + bx + c \]

Alors, la formule du sommet pour la coordonnée x du sommet est :

\[ x_V = \displaystyle -\frac{b}{2a}\]

Comment appliquer la formule des sommets ?

• Étape 1 : Identifiez la fonction quadratique sous sa forme simplifiée. Vous devez avoir quelque chose comme f(x) = ax²+ bx + c
• Étape 2 : à partir de la formule quadratique, vous devez identifier clairement ce que sont a et b
• Étape 3 : À partir de a et b que vous avez identifiés, entrez-les dans la formule xv = -b/2a

Remarquez que si a = 0, la formule sera indéfinie, mais dans ce cas, a ne sera pas nul, puisque nous avons une fonction quadratique, et que le terme qui multiplie x² ne peut pas être nul pour être une fonction quadratique valide.

Pourquoi est-il important de trouver le sommet ?

Le sommet a une propriété très importante : c'est le point où la fonction quadratique atteint son minimum (quand elle s'ouvre vers le haut lorsque a > 0) ou c'est le point où la fonction quadratique atteint son maximum (quand elle s'ouvre vers le bas lorsque a > 0).

Ainsi, en trouvant le sommet, nous obtenons déjà le point extrême de la fonction quadratique.

Exemple : calculer le sommet

Calculez le sommet de la fonction quadratique suivante : \(f(x) = 3x^2+3x+2\)

Solution: Nous devons trouver les coordonnées du sommet de la fonction quadratique \(f(x) = \displaystyle 3x^2+3x+2\).

Pour une fonction quadratique de la forme \(f(x) = a x^2 + bx + c\), la coordonnée x du sommet est calculée à l'aide de la formule suivante :

\[x_V = \displaystyle -\frac{b}{2a}\]

Dans ce cas, nous avons que la fonction pour laquelle nous devons trouver le sommet est \(f(x) = \displaystyle 3x^2+3x+2\), ce qui implique que les coefficients correspondants sont :

\[a = 3\] \[b = 3\] \[c = 2\]

En branchant les valeurs connues de \(a\) et \(b\) dans la formule de la coordonnée x du sommet, on obtient :

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 3} = -\frac{1}{2}\]

Maintenant, nous devons brancher la valeur de \(x_V = \displaystyle -\frac{1}{2}\) dans la fonction quadratique, donc nous obtenons :

\[y_V = f(x_V)\] \[ = 3\cdot \left(-\frac{1}{2}\right)^2+3\cdot \left(-\frac{1}{2}\right)+2=3\cdot\frac{1}{4}+3\cdot \left(-\frac{1}{2}\right)+2=\frac{3}{4}-\frac{3}{2}+2=\frac{5}{4}\]

Par conséquent, la coordonnée x du sommet est \(x_V = \displaystyle -\frac{1}{2}\), et la coordonnée y du sommet est \(y_V = \displaystyle \frac{5}{4}\). Ainsi, le point qui représente le sommet est \( \displaystyle \left(-\frac{1}{2}, \frac{5}{4}\right)\).

Le résultat suivant est obtenu graphiquement :

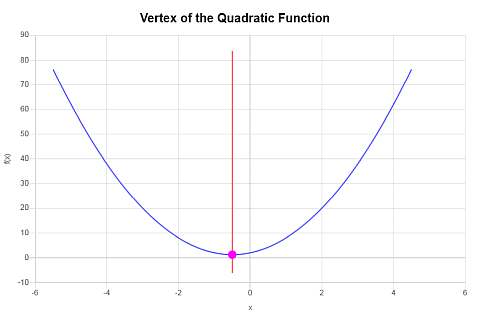
Exemple : application de la formule des sommets

Utilisez la formule du sommet pour calculer les coordonnées du sommet associé à la fonction \(f(x) = x^2 + 4x - \frac{3}{4}\)

Solution: Là encore, nous utilisons la formule suivante :

\[x_V = \displaystyle -\frac{b}{2a}\]

Puisque \(f(x) = \displaystyle x^2+4x-\frac{3}{4}\), ce qui implique que les coefficients correspondants sont :

\[a = 1\] \[b = 4\] \[c = -\frac{3}{4}\]

En branchant les valeurs connues de \(a\) et \(b\) dans la formule de la coordonnée x du sommet, on obtient :

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{4}{2 \cdot 1} = -2\]

Maintenant, nous devons brancher la valeur de \(x_V = \displaystyle -2\) dans la fonction quadratique, donc nous obtenons :

\[y_V = f(x_V)\] \[ = 1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=-2^2+4\cdot \left(-2\right)-\frac{3}{4}=4-8-\frac{3}{4}=-4-\frac{3}{4}=-\frac{19}{4}\]

Par conséquent, la coordonnée x du sommet est \(x_V = \displaystyle -2\), et la coordonnée y du sommet est \(y_V = \displaystyle -\frac{19}{4}\). Ainsi, le point qui représente le sommet est \( \displaystyle \left(-2, -\frac{19}{4}\right)\).

Ceci conclut le calcul.

Exemple : application de vertex

Trouvez le point extrême de la fonction \(f(x) = -2x^2 - 3x + 5\). Ce point extrême est-il un point minimum ou maximum ?

Solution: Nous devons trouver les coordonnées du sommet de la fonction quadratique \(f(x) = \displaystyle -2x^2-3x+5\).

Nous utilisons la formule suivante :

\[x_V = \displaystyle -\frac{b}{2a}\]

Dans ce cas, nous avons que la fonction pour laquelle nous devons trouver le sommet est \(f(x) = \displaystyle -2x^2-3x+5\), donc alors :

\[a = -2\] \[b = -3\]

Cela signifie que :

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{-3}{2 \cdot -2} = -\frac{3}{4}\]

Maintenant, nous devons brancher la valeur de \(x_V = \displaystyle -\frac{3}{4}\) dans la fonction quadratique, donc nous obtenons :

\[y_V = f(x_V)\] \[ = \left(-2\right)\cdot \left(-\frac{3}{4}\right)^2+-3\cdot \left(-\frac{3}{4}\right)+5=\left(-2\right)\cdot\frac{9}{16}+-3\cdot \left(-\frac{3}{4}\right)+5=-\frac{9}{8}+\frac{9}{4}+5=\frac{49}{8}\]

Par conséquent, la coordonnée x du sommet est \(x_V = \displaystyle -\frac{3}{4}\), et la coordonnée y du sommet est \(y_V = \displaystyle \frac{49}{8}\). Ainsi, le point qui représente le sommet est \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\).

On remarque que \(a = -2 < 0\), donc alors la parabole s'ouvre vers le bas, et le point \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\) correspond à un point maximal. C'est-à-dire que la fonction quadratique \(f(x) = \displaystyle -2x^2-3x+5\) atteint un maximum \( \displaystyle \frac{49}{8}\) au point \( x = -\frac{3}{4}\)

Plus de calculatrices quadratiques

On peut faire beaucoup de choses avec les fonctions quadratiques. Vous pouvez calculer la les racines d'une équation quadratique vous pouvez trouver l'axe de symétrie d'une fonction quadratique, et ainsi de suite.

L'application de la formule des sommets est étroitement liée à l'application de la formule quadratique et le Axe de symétrie .