Más sobre este graficador de ecuaciones lineales

Graficar líneas es una habilidad fundamental y esta calculadora te ayudará con eso. Tienes que empezar proporcionando la ecuación lineal quieres graficar.

Puede proporcionar cualquier ecuación lineal explícitamente, por ejemplo, x + 3y = 2, o algo que no esté completamente simplificado como x + 3y = 2/3 x.

Líneas gráficas tiene tantas aplicaciones, que se convierte en una habilidad muy práctica de adquirir. Geométricamente, las líneas tienen una intuición muy simple que facilita su representación gráfica ya que no necesitamos mucha información para especificarlas.

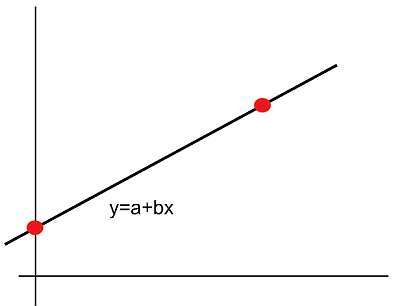
¿cómo graficar ecuaciones lineales?

Puedes usar esto calculadora gráfica para graficar rectas. Si elige hacerlo manualmente, debe tener en cuenta que el enfoque requiere un preámbulo que dependerá del tipo de información proporcionada.

¿cuáles son los pasos para graficar una línea?

• Paso 1: Identifique el tipo de información proporcionada. ¿Tiene una ecuación real provista, tiene dos puntos, un punto y la pendiente, la pendiente y la intersección en y? Evalúe claramente que
• Paso 2: independientemente de la información proporcionada, utilícela para encontrar dos puntos por donde pasa la línea. Para una ecuación dada, resuelva y para x = 0 y x = 1, por ejemplo. Para la pendiente y el intercepto en y, construye la ecuación y = a + bx y encuentra dos puntos. Si tiene un punto y una pendiente, defina y = y1 + b(x-x1) y reemplácelo en x = 0
• Paso 3: Una vez que tenga dos puntos por donde pasa la línea, use una regla para trazar una línea que los atraviese.

Las líneas son súper fáciles de dibujar, solo necesitas ser metódico y ser consciente del tipo de información que tienes disponible.

Incluso si lo haces a mano, siempre es bueno tener una herramienta lineal a mano. calculadora gráfica en línea para comprobar sus resultados.

Líneas gráficas

Graficar líneas tiene muchas aplicaciones. Por ejemplo, puedes resolver un sistema de ecuaciones graficando las líneas correspondientes y viendo dónde se cruzan.

Usando ese método, cuando las líneas son paralelas y no se cruzan, no habrá ninguna solución.

Similar a lo que sucedió con la suma y la resta, la división de fracciones se deriva simplemente de la multiplicación de fracciones: para dividir dos fracciones, simplemente se multiplica la primera por la fracción inversa de la segunda (la fracción inversa se obtiene intercambiando el numerador por el denominador en la fracción).

Otras aplicaciones de los gráficos lineales

Líneas o Gráficos lineales están realmente presentes en todas partes. funciones lineales aparecen en las aplicaciones todo el tiempo, en Cálculo y Optimización, por lo que son realmente útiles.

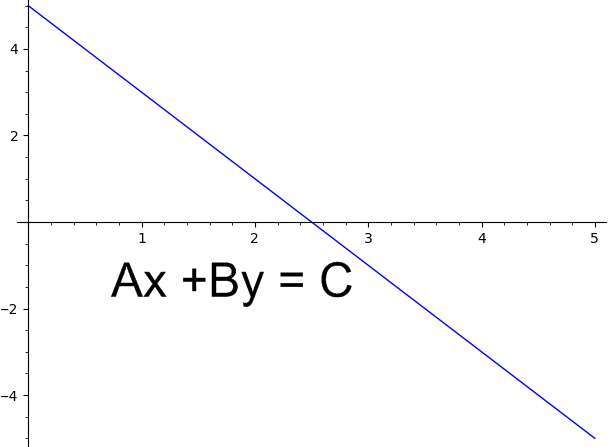
Ejemplo: ejemplo del graficador de ecuaciones lineales

Grafica las siguientes ecuaciones: \(\frac{1}{2}x + \frac{7}{4}y = 0\)

Solución: Necesitamos trabajar con la siguiente ecuación:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Trabajando primero con las constantes:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

El resultado se obtiene colocando (y) en el lado izquierdo y (x) y la constante en el lado derecho:

\[\displaystyle \frac{7}{4}y = -\frac{1}{2}x \]

Luego, el proceso continúa resolviendo para \(y\), y luego dividiendo ambos lados de la ecuación por \(\frac{7}{4}\). Entonces obtenemos:

\[\displaystyle y=-\frac{\frac{1}{2}}{\frac{7}{4}}x\]

y después de la simplificación, el resultado es el siguiente.

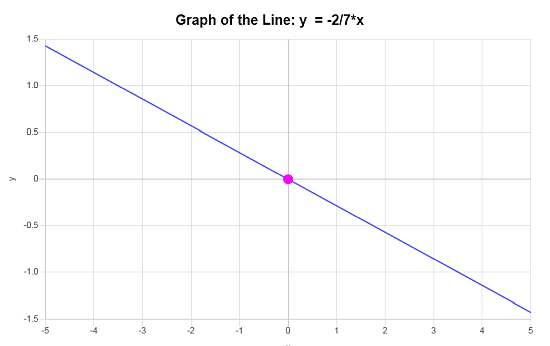
\[\displaystyle y=-\frac{2}{7}x\]

Conclusión : Inferimos que la ecuación de la línea en forma de pendiente-intersección que se basa en los datos disponibles es \(\displaystyle y=-\frac{2}{7}x\), con una pendiente de \(\displaystyle b = -\frac{2}{7}\) y una intersección en y de \(\displaystyle n = 0\).

Por lo tanto, la gráfica de la línea proporcionada es

Ejemplo: ejemplo del graficador de ecuaciones lineales

Obtenga la línea que representa: \(\frac{2}{3}x + \frac{5}{4}y = - \frac{5}{6}x + 2\)

Solución: Nos han proporcionado la siguiente ecuación:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Trabajando con las constantes:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Ahora, poniendo \(y\) en el lado izquierdo y \(x\) y la constante en el lado derecho obtenemos

\[\displaystyle \frac{5}{4}y = \left(\frac{-5}{6}-\frac{2}{3}\right)x +2\]

Ahora bien, el término multiplicando \(y\) es \( \frac{5}{4} - 0 = \frac{5}{4}\), y además desde \( -\frac{5}{6} - \frac{2}{3} = -\frac{3}{2}\), se obtiene lo siguiente

\[\displaystyle \frac{5}{4}y=-\frac{3}{2}x+2\]

Ahora, resolviendo para \(y\), dividiendo ambos lados de la ecuación por \(\frac{5}{4}\), se obtiene lo siguiente

\[\displaystyle y=-\frac{\frac{3}{2}}{\frac{5}{4}}x+\frac{2}{\frac{5}{4}}\]

y simplificando obtenemos finalmente lo siguiente

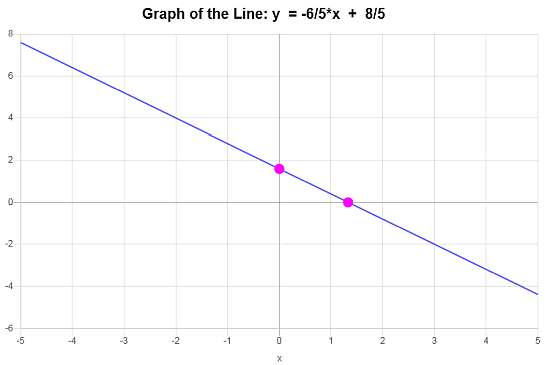
\[\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\]

Conclusión : Con base en los datos proporcionados, concluimos que la ecuación de la línea en forma de pendiente-intersección es \(\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\), con una pendiente de \(\displaystyle b = -\frac{6}{5}\) y una intersección en y de \(\displaystyle n = \frac{8}{5}\).

El gráfico lineal es

Más calculadoras de línea

Las rectas son tan importantes que merecen su propia sección en el libro de Matemáticas. puedes calcular Ecuaciones lineales en diferentes formas, dependiendo de las necesidades específicas.

En última instancia, la determinación de las líneas necesitará dos puntos por los que pasa la línea , que puede darse directa o indirectamente.