Más sobre esta herramienta de calculadora de líneas paralelas.

Hablando geométricamente, dos líneas son paralelas cuando no se cruzan, o son potencialmente la misma línea. Entonces, si Ud. graficar las dos rectas , verás visualmente que no se cruzan. Pero eso puede ser complicado.

Pero, naturalmente, hay formas algebraicas de evaluar si dos líneas son paralelas o no. Una de las formas más sencillas es utilizar el criterio de la pendiente.

¿Cómo determinar si dos rectas son paralelas?

Hay un par de maneras:

1. Gráficamente: mire el gráfico y si las líneas no se cruzan, entonces las líneas son paralelas
2. Algebraicamente: Calcula la pendiente de cada una de las rectas. Si tienen la misma pendiente, las rectas son paralelas.

La ventaja del método gráfico es que es simple e implica solo echar un vistazo al gráfico, pero, naturalmente, para hacerlo, debe construir los gráficos.

Una desventaja del método gráfico es que sus ojos pueden engañarlo. Puede parecer que el Gráfico de líneas no se intersecan, pero tal vez no esté graficando una porción lo suficientemente grande de la línea.

Una ventaja del método algebraico es que es inequívoco. Si las pendientes coinciden, las rectas son paralelas, y si no, las rectas no son paralelas.

La única desventaja del método algebraico es que necesita tomar el trabajo de forma formal calculando la pendiente .

Ecuación de línea paralela

Observa que las rectas que son paralelas tendrán la misma pendiente. Entonces, si la ecuación de una línea es \(y = a x + b\), ¿cuál es la ecuación de la línea paralela?

Primero, no hay una línea paralela, en realidad hay infinitas líneas paralelas, y la ecuación es \(y = a x + c\), para cualquier \(c\).

Como podemos ver, \(y = a x + b\) y \(y = a x + c\) tienen una pendiente igual a "a", por lo que son paralelas.

Si no tiene las líneas ya en formato pendiente-intersección , tu siempre puedes Resolver para y o solución para x es que desea invertir los ejes.

El criterio de la pendiente

Dos rectas son paralelas si tienen la misma pendiente. Esa es la forma más fácil de determinar si dos líneas son paralelas, simplemente calcular la pendiente de ambas líneas y comprobar si son iguales o no.

Una excepción es el caso de dos rectas verticales, que son paralelas, aunque no podemos comparar las pendientes porque no están definidas.

Si tienes algo como el forma de intersección de pendientes de las líneas ya dadas, puedes evaluar directamente si las líneas son paralelas o no. De lo contrario, necesita el paso adicional de calcular las pendientes antes de compararlas.

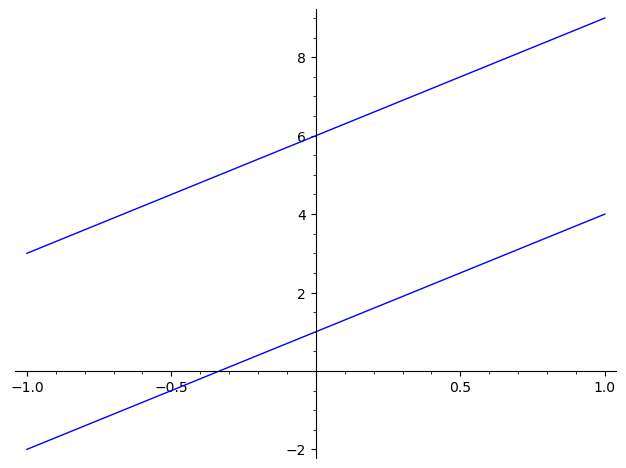
Interpretación geométrica de la gráfica de dos rectas paralelas

Dos rectas paralelas corresponden a un Sistema de Ecuaciones sin soluciones (o soluciones infinitas), donde cada ecuación representa una línea.

Además, cuando las líneas no son paralelas se cortarán en un punto y en un solo punto, lo que corresponde a un Sistema de Ecuaciones con una solución única.

Ejemplo

Determina si las rectas \(2x + 3y = 1\) y \(x + y = 3\) son paralelas.

Respuesta:

Primera Línea: Ponga la primera ecuación en forma de pendiente-intersección

Nos han proporcionado la siguiente ecuación:

\[\displaystyle 2x+3y=1\]

Poniendo \(y\) en el lado izquierdo y \(x\) y la constante en el lado derecho obtenemos

\[\displaystyle 3y = -2x +1\]

Ahora, despejando \(y\), se obtiene lo siguiente

\[\displaystyle y=\frac{-2}{3}x+\frac{1}{3}\]

y simplificando todos los términos que necesitan simplificación, finalmente obtenemos lo siguiente

\[\displaystyle y=-\frac{2}{3}x+\frac{1}{3}\]

Segunda línea: Pon la segunda ecuación en forma de pendiente-intersección

Nos han proporcionado la siguiente ecuación:

\[\displaystyle x+y=3\]

Poniendo \(y\) en el lado izquierdo y \(x\) y la constante en el lado derecho obtenemos

\[\displaystyle y = -x +3\]

Analizar y comparar pendientes

Con base en esta información, encontramos que la pendiente de la primera línea es \(m_1 = -\frac{2}{3}\) y la pendiente de la segunda línea también es \(m_2 = -1\), que son desiguales, entonces las líneas NO son paralelas.

Tenga en cuenta que si la perpendicularidad es lo que está buscando, puede usar este calculadora de líneas perpendiculares . Por definición, las rectas perpendiculares no son paralelas, porque las rectas perpendiculares SIEMPRE tienen pendientes diferentes.