Resolver ecuaciones radicales

Este salculadora de ecuaciones radicales le permite manejar las ecuaciones radicales que usted proporcione, manipulándolas algebraicamente mientras le muestra todos los pasos del proceso.

Este salculadora aceptará cualquier ecuación válida que involucre raíces, como algo realmente simple como 'sqrt(x) = 1', o algo que puede ser mucho más difícil de resolver como 'sqrt(x+3) = x^2 - 1'.

Una vez que se haya proporcionado una ecuación radical válida, básicamente habrá terminado y todo lo que queda por hacer es hacer clic en "Resolver" para que se muestren todos los pasos del proceso.

La solución de la ecuación radical fuerte depende de la efectividad manipulación algebraica de la expresión , para básicamente deshacerse de la parte radical.

¿qué es la ecuación radical?

Una ecuación radical, expresada en términos extremadamente simples, es un tipo de ecuación matemática en el que la incógnita (normalmente x) está dentro de un radical. Por ejemplo

\[\displaystyle \sqrt x = x^2 \]

es una ecuación radical, debido al término \( \sqrt x\), pero la ecuación

\[\displaystyle 2 x = x^2 \]

por ejemplo, NO es una ecuación radical, porque no podemos x información interna de un radical en ninguna parte de la ecuación.

Cómo resolver ecuaciones radicales

Resolver ecuaciones radicales no es difícil si sigues estos pasos:

A veces, independientemente de la agrupación y simplificación adecuadas, no será posible eliminar los radicales por completo o conducirá a una ecuación aún más complicada.

Simplificando ecuaciones radicales

Como mencionamos anteriormente, el cálculo exitoso de ecuaciones que involucran raíces depende en gran medida de poder simplificar radicales . Pero a veces eso no será suficiente, ya que simplificar todos los radicales que aparecen no los hará desaparecer. La forma más común es reducir los radicales y luego aplicar el cuadrado (potencia de 2) para cancelar el radical.

Pero elevar al cuadrado para deshacerse del radical es un doble filo, porque elevando al cuadrado cualquier signo relevante podría desaparecer. Eso es lo que cuando "eliminamos" el radical y encontramos soluciones de una ecuación auxiliar, DEBEMOS verificar que las soluciones auxiliares también sean soluciones de la ecuación original. Muchas veces no lo son.

Otra forma de ver el proceso de eliminación del radical es mediante una sustitución adecuada. Por ejemplo, para la ecuación radical:

\[\displaystyle \sqrt x = x \]

es posible que desees establecer \(u = \sqrt x\), entonces \(u^2 = (\sqrt x)^2 = x\), para que la ecuación original se convierta en la siguiente ecuación auxiliar:

\[\displaystyle \sqrt x = x \Rightarrow u = u^2\]

que es una ecuación polinómica que podemos resolver. Entonces, usando una sustitución llevamos de una ecuación que no sabemos cómo resolver, a resolver una ecuación polinómica que sí sabemos a quién solucionar.

¿por qué nos importan las ecuaciones radicales?

Las ecuaciones radicales son apariciones comunes en álgebra y cálculo, ya que son la base para modelar muchos fenómenos diferentes.

Las funciones radicales son interesantes en términos de sus propiedades y el tipo de crecimiento lento cuando x se acerca al infinito.

Ejemplo: resolver ecuaciones que involucran radicales

Resuelve lo siguiente: \(\sqrt{x} = 2x\)

Solución:

Nos proporciona la siguiente ecuación. Necesitamos resolver esta ecuación que tiene una sola variable, la cual es \(x\), por lo que el objetivo es resolver para \(x\):

\[\sqrt{x}=x^2\]

Observe que el grado del polinomio dado es \(\displaystyle deg(p) = 4\), su coeficiente principal es \(\displaystyle a_{4} = -1\) y su coeficiente constante es \(\displaystyle a_0 = 0\).

Intentando raíces racionales

Candidatos De Raíces Racionales : Dado que el primer término con un coeficiente distinto de cero en \(p(x)\) es \(x\), podemos factorizar este término para obtener

\[\displaystyle p(x) = -x^4+x = x \left(-x^3+1 \right) \]

pero el término entre paréntesis tiene un grado superior a 2, por lo que no existe una fórmula elemental para factorizarlo. Necesitamos probar posibles raíces racionales.

La siguiente tarea es encontrar los números enteros que dividen el coeficiente principal \(a_{3}\) y el coeficiente constante \(a_0\), que se usarán para construir nuestros candidatos a ceros de la ecuación polinómica.

Por lo tanto, dividiendo cada divisor del coeficiente constante \(a_0 = 1\) por cada divisor del coeficiente principal \(a_{3} = -1\), encontramos la siguiente lista de candidatos a ser raíces:

\[\pm \frac{ 1}{ 1}\]

Ahora, todos los candidatos necesitan ser probados para ver si son una solución. De la prueba de cada candidato se obtiene lo siguiente:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -\left(-1^3\right)+1 & = & \displaystyle 2 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle -1^3+1 & = & \displaystyle 0 \\\\ \end{array}\]

División De Polinomios : Como no tenemos suficientes raíces entre los candidatos racionales, dividiremos \(\displaystyle -x^3+1\) por el producto de los factores derivados de las raíces racionales, que es \(\displaystyle \left(x-1\right) \).

Paso 1: El término principal del dividendo \(\displaystyle p(x) = -x^3+1\) es \(\displaystyle -x^3\), mientras que el término principal del divisor \(\displaystyle s(x) = x-1\) es igual a \(\displaystyle x\).

Entonces, el término que necesitamos multiplicar \(x\) para llegar al término principal del dividendo es \(\displaystyle \frac{ -x^3}{ x} = -x^2\), entonces sumamos este término al cociente. Además, multiplicamos esto por el divisor para obtener \(\displaystyle -x^2 \cdot \left(x-1\right) = -x^3+x^2\), que debemos restar al dividendo:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \end{array}\]

Paso 2: Ahora, el término principal del resto actual \(\displaystyle -x^2+1\) es \(\displaystyle -x^2\), y sabemos que el término principal del divisor es \(\displaystyle x\).

Entonces, el término que necesitamos multiplicar \(x\) para llegar al término principal del resto actual es \(\displaystyle \frac{ -x^2}{ x} = -x\), por lo que sumamos este término al cociente. Además, multiplicamos esto por el divisor para obtener \(\displaystyle -x \cdot \left(x-1\right) = -x^2+x\), que debemos restar al recordatorio actual:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \end{array}\]

Paso 3: Ahora, el término principal del resto actual \(\displaystyle -x+1\) es \(\displaystyle -x\), y sabemos que el término principal del divisor es \(\displaystyle x\).

Entonces, el término que necesitamos multiplicar \(x\) para llegar al término principal del resto actual es \(\displaystyle \frac{ -x}{ x} = -1\), por lo que sumamos este término al cociente. Además, multiplicamos esto por el divisor para obtener \(\displaystyle -1 \cdot \left(x-1\right) = -x+1\), que debemos restar al recordatorio actual:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle -1&\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle & \displaystyle x & \displaystyle -1\\[0.3em] \hline \displaystyle & & & & 0\\[0.3em] \end{array}\]

Por lo tanto, el cociente es \(\displaystyle q(x) = -x^2-x-1\) y el resto es \(\displaystyle r(x) = 0\).

Así que después de dividir, hemos avanzado en la factorización con

\[\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\]

Pero ahora, como el cociente encontrado \(\displaystyle -x^2-x-1\) es cuadrático, podemos encontrar sus raíces para ver si podemos factorizarlo en el campo real.

Necesitamos resolver la siguiente ecuación cuadrática \(\displaystyle -x^2-x-1=0\).

Usando la fórmula cuadrática

Para una ecuación cuadrática de la forma \(a x^2 + bx + c = 0\), las raíces se calculan usando la siguiente fórmula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

En este caso, tenemos que la ecuación que necesitamos resolver es \(\displaystyle -x^2-x-1 = 0\), lo que implica que los coeficientes correspondientes son:

\[a = -1\] \[b = -1\] \[c = -1\] \[\Delta = b^2 - 4ac = \displaystyle \left( -1\right)^2 - 4 \cdot \left(-1\right)\cdot \left(-1\right) = -3\]

Como en este caso obtenemos que el discriminante es \(\Delta = \displaystyle -3 < 0\), que es negativo, sabemos que la ecuación dada tiene dos raíces complejas conjugadas diferentes.

Ahora, reemplazando estos valores en la fórmula de las raíces obtenemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(-1\right)\left(-1\right)}}{2\cdot -1} = \displaystyle \frac{1 \pm \sqrt{-3}}{-2}\]

entonces, encontramos que:

\[\displaystyle {x}_1 = \frac{1 - i \sqrt{3}}{-2} = -\frac{1}{2}+\frac{1}{2}\sqrt{3}i\] \[\displaystyle {x}_2 = \frac{1 + i \sqrt{3}}{-2} = -\frac{1}{2}-\frac{1}{2}\sqrt{3}i\]

Entonces, después de encontrar las raíces de la última parte cuadrática, encontramos dos raíces complejas, por lo que no podemos factorizar el término \(-x^2-x-1\) en el campo real, por lo que finalizamos el proceso con \(\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\).

Por lo tanto, resolver \(x\) para la ecuación polinómica dada conduce a las soluciones \(x = \, \)\(0\), \(1\), \(-\frac{1}{2}+\frac{1}{2}\sqrt{3}i\), \(-\frac{1}{2}-\frac{1}{2}\sqrt{3}i\), usando métodos de factorización.

Comprobación de las soluciones auxiliares

Probar estas soluciones de la ecuación polinómica auxiliar muestra que no todas las soluciones candidatas son en realidad una solución de la ecuación original. Las únicas soluciones reales a la ecuación original son:

\[x_1=0 \]
\[x_2=1 \]

Por lo tanto, resolver \(x\) para la ecuación dada conduce a las soluciones \(x=0,\,\,x=1\).

Gráficamente

La siguiente es la representación gráfica de las soluciones obtenidas:

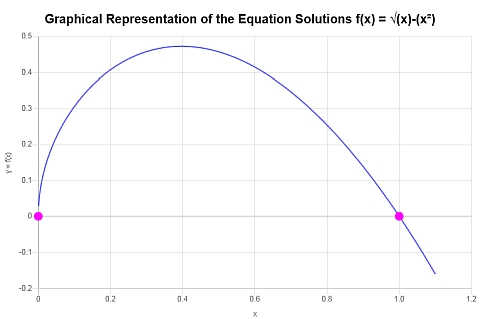
que concluye el cálculo.

Otros calculadoras de ecuaciones útiles

Al resolver ecuaciones radicales, a diferencia del caso en el que es necesario Resolver Ecuaciones Lineales o cuando lo necesites resolver una ecuación cuadrática , cae en la categoría de aquellas ecuaciones que requieren una manipulación algebraica tan inteligente para resolver x.

En otras palabras, no tendrás una cosa del tipo "hazlo de esta manera y siempre funcionará". El tipo de manipulación que realice dependerá de la estructura de la ecuación y puede variar mucho de un caso a otro.

simplificar expresiones El primero siempre es una buena práctica, porque reducirá los términos que pueden estar saturando la estructura general de la ecuación.