So funktioniert ein logarithmischer regressionsrechner

Mit diesem Rechner können Sie eine logarithmische Regression für die Beispieldaten schätzen, die Sie in der entsprechenden Dateneingabetabelle angeben.

Bei gültigen Daten (in diesem Fall kann die X-Variable nur positive Werte annehmen) wird Ihnen nach einem Klick auf „Berechnen“ eine Auswertung aller Prozessschritte sowie ein Scatterplot angezeigt, welches die Qualität der Anpassung veranschaulicht.

Beachten Sie, dass Sie bei dimensionsgültigen Daten immer eine logarithmische Regression ausführen können. Dies bedeutet jedoch nicht, dass die Ergebnisse von guter Qualität sein werden, zumindest was die Anpassung betrifft.

Tools und rechner für die logarithmische regression

Es gibt verschiedene Tools, mit denen Sie Ihre logarithmische Regression schätzen können. Theoretisch können Sie die Dinge manuell erledigen, indem Sie eine Log-Transformation mit einem normalen Taschenrechner durchführen (sogar mit denen, die mit Ihrem Telefon geliefert werden) und dann eine Hilfsgleichung für kleinste Quadrate verwenden, um das Log-Modell zu finden, das lautet

\[ Y = a + b \ln(X) + \varepsilon \]

Sicherlich könnte der manuelle Ansatz mühsam und fehleranfällig sein, um es gelinde auszudrücken. Deshalb ist es eine sehr gute Option, dies zu verwenden Rechner für logarithmische Regression , weil es die ganze Arbeit für Sie erledigt und Ihnen alle Schritte zeigt

Es gibt andere Tools wie Handy-Apps, die alle Arten von Regressionen durchführen sollen, aber Sie müssen es ausprobieren, denn das kann Glückssache sein.

Schritte zum ausführen einer logarithmischen regression

• Schritt 1: Listen Sie die unabhängige Variable (X) und die abhängige Variable (Y) klar auf und stellen Sie sicher, dass beide Variablen die gleiche Stichprobengröße haben
• Schritt 2: Stellen Sie sicher, dass Ihre X-Werte positiv sind, sonst können Sie die Regression nicht ausführen
• Schritt 3: Konstruieren Sie eine neue unabhängige Variable X* = ln(X) durch Anwendung der natürlichen Logarithmustransformation
• Schritt 4: Sie führen nun eine reguläre lineare Regressionsanalyse für X* gegenüber Y durch

Beachten Sie, dass es absolut ratsam ist, einen Rechner oder eine Software zu verwenden, um diagnostische Statistiken zu erhalten, die Ihnen bei der Beurteilung helfen, ob es sinnvoll ist oder nicht, den logarithmisches Regressionsmodell .

Verwendung von excel im vergleich zu speziellen logarithmischen regressionsrechnern

Excel spielt eine wichtige Rolle bei der Durchführung grundlegender statistischer Analysen: Es bietet Ihnen eine übersichtliche und bewährte Benutzeroberfläche zum Ausführen grundlegender Tests, einschließlich der Berechnung der logarithmischen Regression.

Das Hauptproblem von Excel besteht darin, dass es Ihnen keine Lösungsschritte liefert. Dies könnte mit der Einführung von KI-Frameworks wie Copilot hilfreich sein, die Excel wahrscheinlich mit beschreibenden Berechnungsschritten ausstatten würden.

Ergebnisse des regressionsrechners verstehen und interpretieren

Wie jede andere Regressionsanalyse , denn der logarithmische Fall unterscheidet sich nicht darin, dass Sie sich die Statistiken zur Modellanpassung ansehen werden, wie zum Beispiel die F-Statistik um die Signifikanz des Modells insgesamt zu testen und t-Statistiken für die individuelle Signifikanz von Prädiktoren .

Außerdem möchten Sie wahrscheinlich einen Blick auf die erklärten Variationen und Fehler werfen, und die R^2 und angepasste R^2-Koeffizienten , wodurch Sie Schätzungen der durch das Modell erklärten Variation der abhängigen Variable erhalten.

Beispiele für logarithmische regression

Betrachten Sie die Variablen

X: 1, 2, 3, 4, 5

Und: 15, 25, 28, 29, 30

Schätzen Sie ein logarithmisches Regressionsmodell.

Lösung:

Zur Konstruktion eines logarithmischen Regressionsmodells stehen die folgenden Daten für die Variablen X und Y zur Verfügung:

X	Y
1	15
2	25
3	28
4	29
5	30

Die unabhängige Variable, die wir verwenden werden, ist der natürliche Logarithmus von X, und die abhängige Variable ist Y. Um die Regressionskoeffizienten für diese Hilfsregression zu berechnen, muss die folgende Tabelle verwendet werden:

	X	Z = ln(X)	Y	\(Z \cdot Y\)	\(Z^2\)	\(Y^2\)
	1	0	15	0	0	225
	2	0.69	25	17.33	0.48	625
	3	1.1	28	30.76	1.21	784
	4	1.39	29	40.2	1.92	841
	5	1.61	30	48.28	2.59	900
Sum =	15	4.79	127	136.58	6.2	3375

Basierend auf der obigen Tabelle wird Folgendes berechnet:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 4.787491742782}{ 5} = 0.957\]\[\bar Y = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 127}{ 5} = 25.4\]\[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 6.2 - 4.787^2/5 = 1.615\]\[\large SS_{YY} = \sum_{i=1}^{n} Y_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Y_i\right)^2 = 3375 - 127^2/5 = 149.2\]\[\large SS_{ZY} = \sum_{i=1}^{n} Z_i Y_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} Y_i\right) = 136.575 - 4.787 \times 127/5 = 14.973\]

Daher werden auf Grundlage der obigen Berechnungen die Regressionskoeffizienten (die Steigung \(m\) und der y-Achsenabschnitt \(n\)) wie folgt ermittelt:

\[m = \frac{SS_{ZY}}{SS_{ZZ}} = \frac{ 14.973}{ 1.615} = 9.2685\] \[n = \bar Y - \bar Z \cdot m = 25.4 - 0.957 \times 9.2685 = 16.5254\]

Daher stellen wir fest, dass die Regressionsgleichung lautet:

\[\text{ Y} = 16.5254 + 9.2685 \text{ Z}\]

Da jedoch die Hilfsvariable \(Z = \ln(X)\) ist, schlussfolgern wir, dass die logarithmische Regressionsgleichung lautet:

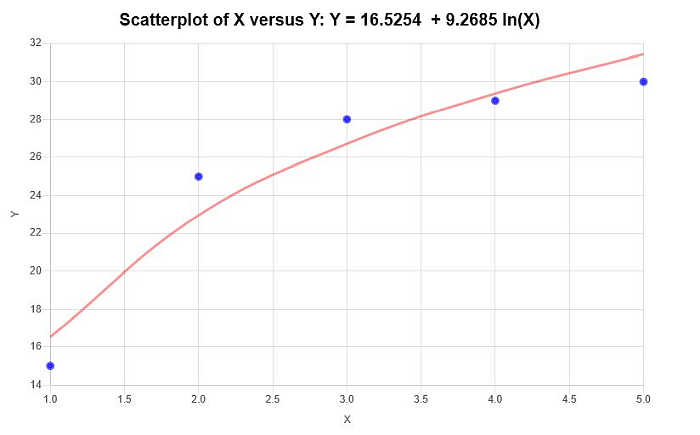
\[\text{ Y} = 16.5254 + 9.2685 \ln(X)\]

Daher ergeben sich auf Grundlage der oben bereitgestellten Informationen das folgende Streudiagramm und Regressionsdiagramm:

Weitere statistikrechner

Sie können auch interessiert sein Berechnung einer exponentiellen Regression oder die Feinheiten einer Polynomregression , die alle in unterschiedlichen Kontexten gelten, basierend auf dem Verhalten der beobachteten Stichprobendaten.

Wahrscheinlich möchten Sie Konstruieren Sie ein Streudiagramm um das empirische Verhalten der Daten zu beurteilen und vorab festzustellen, ob eine logarithmische Regression oder ein anderer Regressionstyp anwendbar ist.