Weitere informationen zum log-log-modell

Mit diesem Rechner können Sie ein Log-Log-Regressionsmodell für die von Ihnen bereitgestellten Daten berechnen. Diese Daten müssen ein geeignetes Abbild eines Log-Log-Modells sein, in dem ein angemessener linearer Assoziationsgrad zwischen ln(X) und ln(Y) bestehen muss.

Sobald Sie gültige Daten angegeben haben, was in diesem Fall positive Daten für X und Y bedeutet, müssen Sie auf die Schaltfläche „Berechnen“ klicken, um zu beginnen, damit Sie alle Schritte des Vorgangs sehen können.

Das Log-Log-Modell hat starke praktische Anwendungen, insbesondere im Bereich der Wirtschaft, in denen es verwendet wird, um Elastizitäten berechnen .

Was ist das log-log-modell?

Das Log-Log-Modell ist, wie der Name vermuten lässt, ein Modell, bei dem \(\ln(X)\) einen signifikanten Grad linearer Assoziation mit \(\ln(Y)\) aufweist. Basierend auf dieser Tatsache, wenn es angemessen ist, ein Regressionsmodell berechnen für diese transformierten Daten, also suchen wir nach Regressionskoeffizienten \(a\) und \(b\), um zu schätzen

\[\displaystyle \ln(Y) = a + b \ln(X)\]

Die Berechnung eines Log-Log-Modells reduziert sich also auf die Berechnung eines regulären Regressionsmodells für die transformierten Daten \(\ln(X)\) und \(\ln(Y)\).

Schritte zur schätzung eines log-log-modells

• Schritt 1: Identifizieren Sie die Variablen eindeutig bei X und Y. Stellen Sie sicher, dass sie die gleiche Stichprobengröße haben und BEIDE alle positiv sind, da Sie sonst kein Log-Log-Modell ausführen können
• Schritt 2: Transformieren Sie die Originaldaten X und Y in die Hilfsdaten ln(X) und ln(x)
• Schritt 3: Verwenden Sie eine reguläre Regressionsmodellgleichung, in der Sie berechnen: Neigung und Y-Abschnitt für Ihre logarithmisch transformierten Daten ln(X) und ln(Y)

Nachdem Sie die entsprechenden Regressionskoeffizienten geschätzt haben, können Sie die Gleichung \(\displaystyle \ln(Y) = a + b \ln(X)\) schreiben, die Sie entweder so lassen oder wie folgt umformen können:

\[\displaystyle Y = e^a \cdot x^b \]

Interpretation des log-log-modells

Wie können wir die gefundenen Koeffizienten so interpretieren, wie wir es bei der üblichen Regression aus der Sicht der marginalen Veränderung getan haben? Bei einem typischen Regressionsproblem können Sie den Steigungskoeffizienten als durchschnittliche Zunahme der Y-Variablen interpretieren, wenn die X-Variable um eine Einheit erhöht wird.

In einem Log-Log-Modell funktioniert es nicht ganz so, aber es hat eine ähnliche Randinterpretation. Tatsächlich können wir es in einem \(\displaystyle \ln(Y) = a + b \ln(X)\)-Modell wie folgt interpretieren:

Eine Steigerung von 1% bei X bringt eine durchschnittliche Steigerung von b% bei Y . Wenn \(b\), entspricht dies natürlich einer Verringerung.

Warum wir dieses modell verwenden

Ein sehr wichtiger Grund ist, dass es in der Wirtschaft häufig Anwendung findet. Die Idee, dass die Preiselastizität der Nachfrage einfach durch die Berechnung des Steigungskoeffizienten eines Log-Log-Modells ermittelt werden kann, macht es relevant genug, um es zu berücksichtigen.

Darüber hinaus findet die Idee einer relativen Grenzänderung in der Nutzentheorie der Wirtschaftswissenschaften zahlreiche weitere Anwendungsmöglichkeiten und ist somit ein äußerst praktisches und anwendbares Modell.

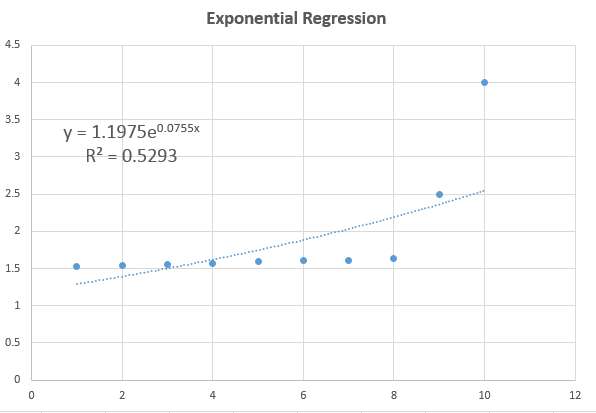
Beispiel für eine log-log-regressionsberechnung

Betrachten Sie die folgenden Daten für X und Y:

X: 1, 2, 3, 4, 5, 6, 7

Y: 10, 11,1, 13, 15,6, 16,8, 20, 22,4

Schätzen Sie das entsprechende Log-Log-Modell und stellen Sie ein geeignetes Streudiagramm dar

Lösung:

womit die Berechnung abgeschlossen ist.

Weitere regressionsrechner

Sie müssen beurteilen, ob Sie eine signifikanter Korrelationskoeffizient zwischen ln(X) und ln(Y) vor dem Ausführen des Modells. Es ist auch eine gute Idee, Machen Sie einen Streuplot der Daten, um zu sehen, ob sie mit den Erwartungen einer Log-Log-Assoziation übereinstimmen.

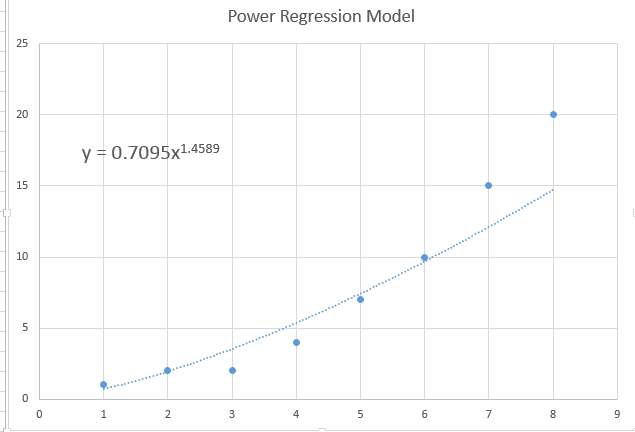
Oftmals ist nur eine geringfügige Krümmung vorhanden und die Daten zeigen ein nahezu flaches Muster, was auch mit einem traditionellen Regressionsmodell übereinstimmt, es kann aber auch ein Potenz-Regressionsmodell mit sehr kleinen Koeffizienten.