Zeri polinomiali

Questa calcolatrice ti consentirà di calcolare le radici polinomiali di qualsiasi polinomio valido che fornisci. Questo polinomio può essere qualsiasi polinomio di grado 1 o superiore.

Ad esempio, puoi fornire un polinomio cubico, come p(x) = x^3 + 2x^2 - x + 1, oppure puoi fornire un polinomio con coefficienti non interi, come p(x) = x^ 3 - 13/12 x^2 + 3/8 x - 1/24.

Dopo aver fornito alla calcolatrice un polinomio valido per il quale si desidera calcolare le sue radici, è possibile fare clic sul pulsante "Calcola" e si vedrà un'esecuzione passo dopo passo del processo.

Va detto che il processo coinvolge solo metodi elementari utilizzati per trovare le radici, che include il Teorema zero razionale e Divisione polinomiale , così come l'utilizzo di formula quadratica quando appropriato.

Non esiste un metodo generale per trovare TUTTE le radici di TUTTI i possibili polinomi di livello superiore a 5, quindi questa calcolatrice troverà solo le radici che possono essere ottenute con questi metodi elementari menzionati.

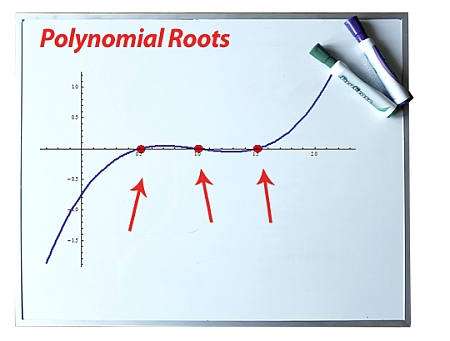
Qual è la radice di un polinomio?

Dato un funzione polinomiale \(p(x)\), diciamo che \(x\) è una radice del polinomio se:

\[\displaystyle p(x) = 0 \]

In parole povere le radici di un polinomio sono i punti in cui la funzione polinomiale \(p(x)\) attraversa l'asse x. Questa è una buona rappresentazione per farsi un'idea, ma non è del tutto precisa perché alcune radici potrebbero essere numeri complessi. Quindi, una vera radice sarà un punto in cui \(p(x)\).

Si osservi che le radici del polinomio sono anche chiamate zeri polinomiali.

Quali sono i passaggi per trovare gli zeri di un polinomio?

• Fase 1: Identifica l'espressione con cui vuoi lavorare. Assicurati che sia un polinomio e semplifica il più possibile
• Passo 2: Useremo il fattorizzazione polinomiale approccio per trovare la sua radice
• Smusso 3: Inizia a cercare di trovare radici elementari (razionali) con il Teorema zero razionale , e usa Divisione polinomiale per ridurre il polinomio originale, se possibile
• Passaggio 4: Se il passaggio 3 ha funzionato ed è possibile ridurre il polinomio originale, ripetere i passaggi precedenti per provare a fattorizzare il polinomio ridotto

Di solito non è facile, e può essere computazionalmente intenso, e non è garantito che funzioni, ma è il miglior approccio possibile se ci limitiamo a usare metodi elementari.

Il factoring è l'unico modo per trovare radici

Non proprio, ma le cose vanno mano nella mano. Il teorema dei fattori afferma che \(x - a\) è un fattore di un polinomio \(p(x)\) se e solo se \(p(a) = 0\). Quindi, in altre parole, radici e fattori sono intimamente legati.

Ora, per polinomi di grado 2 (questo è, polinomi quadratici ) possiamo usare una formula esplicita, che è la ben nota formula quadratica .

Lo stesso accade per i gradi 3 e 4, anche se le formule sono tutt'altro che elementari. Ma per il grado 5 e superiore, non esiste una formula del genere, un risultato chiave dimostrato da Galois e Abel. Quindi non c'è speranza di trovare una "formula generale", ed è per questo che l'uso è più lassista fattorizzazione polinomiale approccio.

Errori comuni da evitare

Spesso gli studenti si sentono frustrati perché non riescono a trovare le radici di un dato funzione polinomiale , dicono \(p(x) = x^3+2 x^2-x+1 \), ma devono affrontare il fatto che non tutti i polinomi potranno essere risolti utilizzando strumenti elementari.

Certo, c'è una formula per risolvere \(x^3+2 x^2-x+1 = 0 \), ma non è elementare, e non ci si aspetta che gli studenti la conoscano.

Suggerimenti per il successo

Cerca sempre di fare una mappa mentale di quale sarà la tua strategia: prendi nota del polinomio che hai, il suo grado, il suo coefficiente principale e il coefficiente costante.

Traccia il polinomio se puoi, per avere un'idea del suo comportamento. Ci sono fattorizzazioni ovvie che puoi usare? Usali. Ricorda sempre fattori = radici.

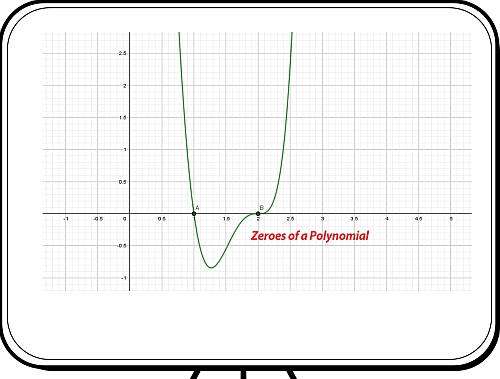
Esempio: zeri di un polinomio

Quali sono gli zeri di : \(x^5 + x^4 - x^3 + x^2 - x + 1\)?

Soluzione: Per questo esempio ci viene fornito il seguente polinomio: \(\displaystyle p(x) = x^5+x^4-x^3+x^2-x+1\). Useremo l'approccio del factoring per trovare le radici.

Semplificazione non necessaria: L'espressione polinomiale fornita è già semplificata, quindi non c'è niente per semplificarla ulteriormente.

Si può notare che il grado del polinomio fornito è \(\displaystyle deg(p) = 5\). Inoltre, il suo coefficiente principale è \(\displaystyle a_{5} = 1\) e il suo coefficiente costante è uguale a\(\displaystyle a_0 = 1\).

Ora cerchiamo i numeri interi che dividono il coefficiente principale \(a_{5}\) e il coefficiente costante \(a_0\), che viene utilizzato per trovare candidati razionali .

▹ I divisori di \(a_{5} = 1\) sono: \(\pm 1\).

▹ I divisori di \(a_0 = 1\) sono: \(\pm 1\).

Pertanto, dividendo tutti i fattori del termine costante \(a_0 = 1\) per tutti i divisori di \(a_{5} = 1\), otteniamo il seguente elenco di potenziali radici:

\[\pm \frac{ 1}{ 1}\]

Ora, tutte le potenziali soluzioni devono essere valutate. I risultati ottenuti dal test di ciascun candidato sono i seguenti:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle \left(-1\right)^5+\left(-1\right)^4-\left(-1\right)^3+\left(-1\right)^2-\left(-1\right)+1 & = & \displaystyle 4 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 1^5+1^4-1^3+1^2-1+1 & = & \displaystyle 2 \ne 0 \\\\ \end{array}\]

Poiché non sono state identificate radici razionali attraverso l'ispezione manuale, non è possibile un'ulteriore semplificazione utilizzando tecniche di base e il processo termina con questo passaggio.

Conclusione : Di conseguenza, non è stata ottenuta alcuna semplificazione e nessuna radice del polinomio è stata identificata attraverso tecniche di base

Esempio: calcolo delle radici di una funzione quadratica

Calcolare le soluzioni di: \(3x^2 - 2x - 4 = 0\).

Soluzione: Dobbiamo risolvere l'equazione quadratica data \(\displaystyle 3x^2-2x-4=0\).

Le radici per un'equazione quadratica della forma \(a x^2 + bx + c = 0\) vengono calcolate utilizzando la seguente equazione:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In questo contesto, l'equazione che deve essere risolta è \(\displaystyle 3x^2-2x-4 = 0\), indicando che i coefficienti corrispondenti sono:

\[a = 3\] \[b = -2\] \[c = -4\]

Innanzitutto, determineremo la natura delle radici calcolando il discriminante. Il discriminante è calcolato come segue:

\[\Delta = b^2 - 4ac = \displaystyle \left( -2\right)^2 - 4 \cdot \left(3\right)\cdot \left(-4\right) = 52\]

Poiché in questo caso otteniamo che il discriminante è \(\Delta = \displaystyle 52 > 0\), che è positivo, allora l'equazione ha due radici reali diverse.

Da questo otteniamo:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(3\right)\left(-4\right)}}{2\cdot 3} = \displaystyle \frac{2 \pm \sqrt{52}}{6}\]

allora, troviamo che:

\[ x_1 = \frac{2}{6}-\frac{1}{6}\sqrt{52}=\frac{2}{6}-\frac{1}{6}\cdot 2\sqrt{13}=\frac{2}{6}-\frac{1}{3}\sqrt{13}=\frac{1}{3}-\frac{1}{3}\sqrt{13} \] \[x_2 = \frac{2}{6}+\frac{1}{6}\sqrt{52}=\frac{2}{6}+\frac{1}{6}\cdot 2\sqrt{13}=\frac{2}{6}+\frac{1}{3}\sqrt{13}=\frac{1}{3}+\frac{1}{3}\sqrt{13}\]

Troviamo che l'equazione \( \displaystyle 3x^2-2x-4 = 0 \), ha due radici reali, quindi:

\[\displaystyle 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\]

quindi il polinomio originale viene scomposto come \(\displaystyle p(x) = 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right) \), che completa la fattorizzazione.

Conclusione : Pertanto, la fattorizzazione che cerchiamo è data da:

\[\displaystyle p(x) = 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\]

Le radici trovate sono \(-\frac{1}{3}\sqrt{13}+\frac{1}{3}\) e \(\frac{1}{3}\sqrt{13}+\frac{1}{3}\) .

Esempio: zeri polinomiali

Calcola gli zeri del seguente polinomio: \(p(x)= x^3 - \frac{13}{12} x^2 + \frac{3}{8} x - \frac{1}{24} \).

Soluzione: Infine, in questo esempio abbiamo: \(\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24}\).

Primo Passo: L'espressione polinomiale fornita è irriducibile, quindi non c'è nulla da semplificare. Possiamo procedere a fattorizzarlo.

Si osservi che il grado del polinomio dato è \(\displaystyle deg(p) = 3\), il suo coefficiente principale è \(\displaystyle a_{3} = 1\) e il suo coefficiente costante è \(\displaystyle a_0 = -\frac{1}{24}\).

Radici Razionali : Cercheremo prima di trovare radici razionali semplici, con il teorema dello zero razionale.

Il compito successivo è trovare i numeri interi che dividono il coefficiente principale \(a_{3}\) e il coefficiente costante \(a_0\), che verranno utilizzati per costruire i nostri candidati come zeri dell'equazione polinomiale.

Uso: In questo caso, osserviamo che per avere sia il coefficiente costante che quello principale dobbiamo amplificare entrambi i lati dell'equazione con \(24\). L'equazione equivalente è:

\[24x^3-26x^2+9x-1 = 0\]

▹ I divisori di \(a_{3} = 24\) sono: \(\pm 1,\pm 2,\pm 3,\pm 4,\pm 6,\pm 8,\pm 12,\pm 24\).

▹ I divisori di \(a_0 = -1\) sono: \(\pm 1\).

Pertanto, dividendo ogni divisore del coefficiente costante \(a_0 = -1\) per ogni divisore del coefficiente principale \(a_{3} = 24\), troviamo il seguente elenco di candidati radici:

\[\pm \frac{ 1}{ 1},\pm \frac{ 1}{ 2},\pm \frac{ 1}{ 3},\pm \frac{ 1}{ 4},\pm \frac{ 1}{ 6},\pm \frac{ 1}{ 8},\pm \frac{ 1}{ 12},\pm \frac{ 1}{ 24}\]

Ora, tutti i candidati devono essere testati per vedere se sono una soluzione. Quanto segue si ottiene testando ogni candidato:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle 24\cdot \left(-1\right)^3-26\cdot \left(-1\right)^2+9\cdot \left(-1\right)-1 & = & \displaystyle -60 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 24\cdot 1^3-26\cdot 1^2+9\cdot 1-1 & = & \displaystyle 6 \ne 0 \\\\ x & = & \displaystyle -\frac{1}{2} &:&    & \displaystyle 24\left(\frac{-1}{2}\right)^3-26\left(\frac{-1}{2}\right)^2+9\left(-\frac{ 1}{ 2}\right)-1 & = & \displaystyle -15 \ne 0 \\\\ x & = & \displaystyle \frac{1}{2} &:&    & \displaystyle 24\left(\frac{1}{2}\right)^3-26\left(\frac{1}{2}\right)^2+9\cdot \frac{1}{2}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{3} &:&    & \displaystyle 24\left(\frac{-1}{3}\right)^3-26\left(\frac{-1}{3}\right)^2+9\left(-\frac{ 1}{ 3}\right)-1 & = & \displaystyle -\frac{70}{9} \ne 0 \\\\ x & = & \displaystyle \frac{1}{3} &:&    & \displaystyle 24\left(\frac{1}{3}\right)^3-26\left(\frac{1}{3}\right)^2+9\cdot \frac{1}{3}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{4} &:&    & \displaystyle 24\left(\frac{-1}{4}\right)^3-26\left(\frac{-1}{4}\right)^2+9\left(-\frac{ 1}{ 4}\right)-1 & = & \displaystyle -\frac{21}{4} \ne 0 \\\\ x & = & \displaystyle \frac{1}{4} &:&    & \displaystyle 24\left(\frac{1}{4}\right)^3-26\left(\frac{1}{4}\right)^2+9\cdot \frac{1}{4}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{6} &:&    & \displaystyle 24\left(\frac{-1}{6}\right)^3-26\left(\frac{-1}{6}\right)^2+9\left(-\frac{ 1}{ 6}\right)-1 & = & \displaystyle -\frac{10}{3} \ne 0 \\\\ x & = & \displaystyle \frac{1}{6} &:&    & \displaystyle 24\left(\frac{1}{6}\right)^3-26\left(\frac{1}{6}\right)^2+9\cdot \frac{1}{6}-1 & = & \displaystyle -\frac{1}{9} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{8} &:&    & \displaystyle 24\left(\frac{-1}{8}\right)^3-26\left(\frac{-1}{8}\right)^2+9\left(-\frac{ 1}{ 8}\right)-1 & = & \displaystyle -\frac{165}{64} \ne 0 \\\\ x & = & \displaystyle \frac{1}{8} &:&    & \displaystyle 24\left(\frac{1}{8}\right)^3-26\left(\frac{1}{8}\right)^2+9\cdot \frac{1}{8}-1 & = & \displaystyle -\frac{15}{64} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{12} &:&    & \displaystyle 24\left(\frac{-1}{12}\right)^3-26\left(\frac{-1}{12}\right)^2+9\left(-\frac{ 1}{ 12}\right)-1 & = & \displaystyle -\frac{35}{18} \ne 0 \\\\ x & = & \displaystyle \frac{1}{12} &:&    & \displaystyle 24\left(\frac{1}{12}\right)^3-26\left(\frac{1}{12}\right)^2+9\cdot \frac{1}{12}-1 & = & \displaystyle -\frac{5}{12} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{24} &:&    & \displaystyle 24\left(\frac{-1}{24}\right)^3-26\left(\frac{-1}{24}\right)^2+9\left(-\frac{ 1}{ 24}\right)-1 & = & \displaystyle -\frac{91}{64} \ne 0 \\\\ x & = & \displaystyle \frac{1}{24} &:&    & \displaystyle 24\left(\frac{1}{24}\right)^3-26\left(\frac{1}{24}\right)^2+9\cdot \frac{1}{24}-1 & = & \displaystyle -\frac{385}{576} \ne 0 \\\\ \end{array}\]

Ma poiché abbiamo trovato tutte le radici richieste tra i candidati razionali, troviamo che \(\displaystyle x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right) \), allora:

\[\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right) \]

che completa il processo di fattorizzazione.

Risultato : Pertanto, la fattorizzazione finale è:

\[\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right)\]

Pertanto, le radici trovate sono \(\frac{1}{2}\),\(\frac{1}{3}\) e \(\frac{1}{4}\) .

Altri utili calcolatori polinomiali

Trovare gli zeri di un polinomio è uno dei vertici dell'algebra, nella misura in cui il teorema fondamentale dell'algebra riguarda l'esistenza di n radici per un polinomio di grado n. Quelle radici non saranno necessariamente tutte reali e alcune di esse (o tutte) potrebbero essere numeri complessi.

In definitiva, quasi ogni singolo problema di algebra e calcolo può essere ridotto alla ricerca delle radici di un polinomio, compresa la risoluzione equazioni polinomiali , come quelli che troveresti, ad esempio, quando cerchi il file intersezione tra i grafici di \(y = x^2\) e \(y = x^3\).