Funzioni polinomiali

Questo calcolatrice di funzioni polinomiali ti aiuterà a calcolare le funzioni polinomiali, calcolando e semplificando qualsiasi espressione polinomiale che fornisci.

È possibile fornire qualsiasi tipo di espressione che coinvolga i polinomi e il calcolo verrà condotto e verranno eseguiti i passaggi di semplificazione necessari, in modo da lasciare una funzione polinomiale nella sua forma più compatta. Quindi, verrà fornito un grafico polinomiale

Quindi, una volta fornita un'espressione polinomiale valida, è possibile fare clic sul pulsante in basso, il pulsante "Calcola", e verranno visualizzati tutti i passaggi richiesti del processo.

L'algebra delle frazioni implica la conversione di frazioni come l'uso del denominatore comune e l'uso di regole aritmetiche di base. Tutto sommato, il processo di calcolo può essere laborioso, sebbene possa essere eseguito sistematicamente, senza troppi problemi.

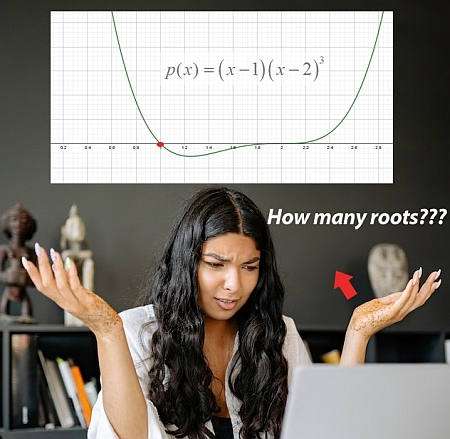
Cos'è una funzione polinomiale?

I polinomi, nella spiegazione più semplice, sono le funzioni che consistono solo di potenze di \(x\), eventualmente moltiplicate per costanti numeriche, che vengono sommate (o sottratte) tra loro. Ad esempio, \(p(x) = x^3 + 2x^2 + 1\) è una funzione polinomiale, poiché consiste delle potenze di \(x\) moltiplicate per costanti, sommate. In questo caso, \(1 = x^0\) quindi una costante è anche una potenza di \(x\). :

In generale, una funzione polinomiale ha la seguente forma:

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

con \(a_n \ne 0\). In questo caso diciamo che il grado di polinomio (o il suo ordine) è \(n\), che è la massima potenza presente nella funzione polinomiale.

Inoltre, il coefficiente \(a_n\) è chiamato il coefficiente direttivo , e \(a_n x^n\) è chiamato il termine principale . Il coefficiente principale e il grado di un polinomio determineranno il suo comportamento finale (questo è il comportamento quando il valore assoluto di x è grande).

Quali sono i passaggi per lavorare con una funzione polinomiale?

• Fase 1: Identifica chiaramente l'espressione con cui vuoi lavorare, espandi e semplifica
• Passo 2: Controlla se i termini che coinvolgono la variabile x corrispondono solo a potenze di x, altrimenti ti fermi, non è un polinomio
• Smusso 3: Assicurati che tutte le potenze di x siano moltiplicate per costanti (che potrebbero essere '1') e che quei termini appaiano come aggiunti o sottratti nell'espressione

È importante assicurarsi di avere una funzione polinomiale, in modo da poter applicare risultati esclusivi ai polinomi, ad esempio teorema dei fattori , il teorema del resto e Teorema zero razionale , che sono estremamente utili per trovare le soluzioni alle equazioni polinomiali, che sono ampiamente utilizzate in diverse applicazioni.

Inoltre, il vantaggio di trattare con funzioni polinomiali è che puoi condurre facilmente divisione di polinomi , utilizzando Divisione Lunga , o Divisione sintetica nel caso in cui il divisore sia lineare.

Esistono funzioni polinomiali importanti?

Infatti. Ci sono i famigerati polinomi di grado 2, che chiamiamo polinomi quadratici , che sono ampiamente studiati in Algebra di base. La ragione di ciò è che possono essere completamente analizzati utilizzando formule precise. Ad esempio, hai un formula per il vertice , e la famosa formula quadratica è usata per trovare le radici di polinomi quadratici :

\[\displaystyle x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

Ci sono anche i polinomi di grado 2, che chiamiamo polinomi cubici , che hanno anche formule esplicite, ma che di solito sono ritenute più complesse e in genere non sono trattate nei corsi di algebra di base.

Cosa so del comportamento finale di un polinomio?

Il comportamento finale di un polinomio dipenderà in ultima analisi dal polinomio stesso, ma si possono dire alcune cose in base al loro grado

• Fatto 1: Per i polinomi quadratici, il grafico si apre verso l'alto (se il coefficiente principale è positivo) o verso il basso (se il coefficiente principale è negativo) e la funzione converge a infinito o meno infinito (a seconda del segno del coefficiente principale) su entrambi i lati
• Fatto 2: Per i polinomi con grado dispari (ad esempio, con grado 3) avranno almeno una radice reale e la funzione converge a infinito da un lato e a meno infinito dall'altro
• Fatto 3: Per i polinomi con grado pari (ad esempio, con grado 4), non ci saranno necessariamente radici reali (un punto che il grafico attraversa nell'asse x), e la funzione converge a infinito o meno infinito (a seconda di il segno del coefficiente principale) su entrambi i lati

Quindi, i polinomi sono grandi per valori grandi di x e se i loro valori sono positivi o negativi per valori positivi di x (nel loro comportamento finale) dipende dal segno del coefficiente principale.

Suggerimenti: quali sono i vantaggi dell'utilizzo di un calcolatore di funzioni polinomiali

I calcolatori polinomiali possono assicurarti di arrivare alla risposta giusta. Infatti, calcoli polinomiali non sono complicati, ma possono essere ingombranti e non è difficile sbagliare.

Evita gli errori algebrici assicurandoti di controllare il tuo lavoro con questo calcolatore, in modo da poter garantire la coerenza della risposta finale e i passaggi utilizzati per arrivarci.

Esempio: funzione polinomiale

Calcolare la seguente funzione polinomiale \((x-3)(x-1)(x-4)\)

Soluzione: Ci viene fornita la seguente espressione polinomiale che dobbiamo calcolare: \(\displaystyle (x-3)(x-1)(x-4)\).

Si ottiene il seguente calcolo:

che conclude il processo di semplificazione polinomiale.

Si ottiene il seguente grafico per \(\displaystyle x^3-8x^2+19x-12\) sull'intervallo \([-5, 5]\):

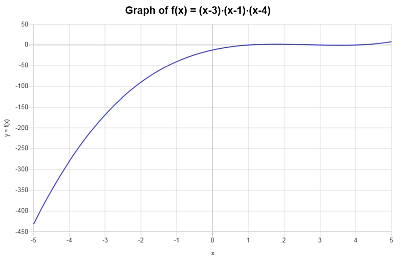
Esempio: calcolo della funzione polinomiale

È una funzione polinomiale: \(\frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})\)

Soluzione:

Ci viene fornita la seguente espressione polinomiale che dobbiamo calcolare: \(\displaystyle \frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})\).

Si ottiene il seguente calcolo:

che conclude il processo di semplificazione.

Graficamente si ottiene per la funzione semplificata \(\displaystyle \frac{1}{3}x^3+\frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}\) sull'intervallo \([-5, 5]\):

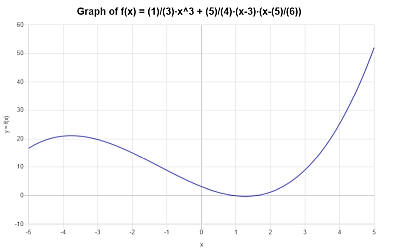
Esempio: utilizzo di un calcolatore polinomiale

Calcola \( x^2 - (2x - 1)x \).

Soluzione: In questo ultimo esempio abbiamo \(\displaystyle x^2 - (2x - 1)x \), che dobbiamo semplificare.

Si ottiene il seguente calcolo:

che pone fine alla semplificazione.

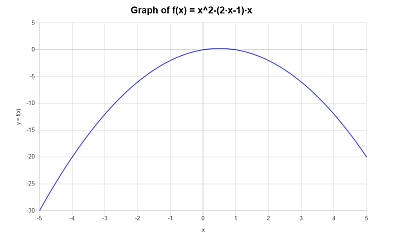
Si ottiene il seguente grafico per \(\displaystyle -x^2+x\) sull'intervallo \([-5, 5]\):

Altri calcolatori di algebra

Le funzioni polinomiali sono letteralmente il pezzo centrale in Algebra. Per applicazioni di base, polinomi quadratici giocherà un ruolo chiave e Economia, Fisica e Ingegneria.

Le funzioni polinomiali hanno proprietà estremamente potenti, in particolare per quanto riguarda il calcolo di radici polinomiali , che hanno un forte significato nelle applicazioni.