Il concetto di funzione è estremamente importante ed è assolutamente onnipresente in matematica. Questo è il motivo per cui dobbiamo dargli un bel ripasso, prima di tentare di comprendere alcune delle chicche che verranno in seguito quando approfondiremo argomenti di calcolo, come la differenziazione e l'integrazione.

CHE COS'È UN SET?

Il primo elemento che dobbiamo capire è il concetto di a impostato . Un set è semplicemente una raccolta di elementi. Quindi, un insieme è definito molto semplicemente in modo da sapere quali elementi appartengono all'insieme e quali no. Sembra essere un compito semplicissimo e la teoria degli insiemi dovrebbe essere ridotta semplicemente ad avere regole univoche per determinare quali elementi appartengono a un insieme.

Ad esempio, definiamo l'insieme di numeri pari e lo chiamiamo \(E\). Perché è anche un set? Perché ha una regola univoca per determinare quali elementi appartengono a \(E\): Un numero reale \(x\) appartiene a \(E\) se è divisibile per 2. La regola funziona in modo univoco per ogni singolo numero reale determinando se appartiene o meno a \(E\). Perché dico "in modo inequivocabile" e continuo a ripetere. Perché è importante. Inequivocabilmente significa che non c'è modo di concludere che un dato \(x\) appartenga e non appartenga a \(E\). Purtroppo a volte le cose vanno oltre la nostra immaginazione. Contrariamente alla nostra intuizione, un insieme definibile con una semplice regola di appartenenza può portare a una classificazione di appartenenza ambigua (contraddittoria), come mostra Bertrand Russell nel suo famoso paradosso. Russell ha mostrato che dovrebbe essere usata una definizione più accurata di cosa sia un set.

A tutti gli effetti, penseremo a un insieme come a un insieme di elementi, definibili da una regola di appartenenza .

QUAL È IL PRODOTTO DI DUE SET?

Siano \(A\) e \(B\), nel contesto della definizione data sopra. Il prodotto \(A\times B\) di due set è un altro set, che è definito come l'insieme di tutte le possibili coppie ordinate della forma \(\left( a, b \right)\), dove \(a\) appartiene a \(A\) e \(b\) appartiene a \(B\). Quindi, \(A\times B\) è un insieme, ei suoi elementi sono coppie ordinate della forma \(\left( a ,b \right)\). Non lasciare che quella notazione ti impressioni. Quando dico "coppie ordinate della forma \(\left( a, b \right)\)", il simbolo \(\left( a, b \right)\) è un simbolo inventato, per indicare un elemento composto da due entità \(a\) e \(b\) e identificare il primo elemento come \(a\) e il secondo elemento come \(b\) . Questo è tutto. Invece di \(\left( a,b \right)\), avremmo potuto scegliere il simbolo \(a\_b\) e avrebbe funzionato bene.

Dovrai perdonarmi, ma devo scrivere la definizione matematica del prodotto di due insiemi (possiamo anche moltiplicare gli insiemi ... cosa pensavi, ci fermeremmo solo con i numeri, eh?):

\(A\times B=\left\{ \left( a,b \right):\,\,\,a\in A,\,\,\,b\in B \right\}\)

Il motivo per cui scrivo la definizione è che tu la guardi e riconosci come usando una notazione molto compatta stiamo dicendo esattamente lo stesso come l'ho definita con le parole nel paragrafo sopra. Spero che scioglierai un po 'di paura per la lettura di dichiarazioni di matematica. I matematici a volte possono essere persone funky, ma trovano notazioni buone, univoche e compatte. E di conseguenza, il linguaggio matematico è SUPER facile da leggere. Destra? Destra? Per favore dimmi che ho ragione ...

Una nota a margine, per ragioni storiche, il prodotto di due insiemi \(A\times B\) è normalmente indicato come a prodotto cartesiano .

ORA, LA DEFINIZIONE DI UNA FUNZIONE (FINALMENTE)

Ok, ho mentito, c'è ancora un passaggio prima di definire cos'è una funzione. Dobbiamo definire il concetto di relazione . Cos'è una relazione? Al di là del suo uso comune come parola inglese, una relazione è semplicemente un sottoinsieme di un prodotto cartesiano. QUALSIASI sottoinsieme di un prodotto cartesiano è una relazione. Quindi, se \(A\) e \(B\) sono insiemi, un insieme \(R\) è una relazione se \(R\subseteq A\times B\). Poiché qualsiasi insieme può essere considerato come un sottoinsieme di se stesso, tutti i prodotti cartesiani sono relazioni stesse.

Mettilo su una cornice:

Una relazione è un insieme che è un sottoinsieme di un prodotto cartesiano

Diventiamo più grafici. Considera l'insieme \(A=\left[ 0,1 \right]\) (che è tutti i numeri reali che sono maggiori o uguali a 0 e sono anche minori o uguali a 1). Qual è il prodotto cartesiano \(A\times A\)? Riprendiamo a pappagallo ciò che abbiamo appena imparato. Il prodotto cartesiano \(A\times A\) è \(\left[ 0,1 \right]\times \left[ 0,1 \right]\) in questo caso è l'insieme di tutte le coppie\(\left( x, y \right)\), dove sia \(x\) che \(y\) appartengono a \(\left[ 0,1 \right]\). I prodotti cartesiani sono in genere facili da rappresentare graficamente. Guarda la regione ombreggiata di seguito:

Ora, cosa farebbe una relazione? Possiamo "ritagliare" tutto ciò che vogliamo nella regione ombreggiata sopra, e ciò che rimane è una relazione in \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). Ad esempio, possiamo tagliare gli "angoli" per ottenere la seguente sottoregione:

La regione (insieme) sopra è una relazione. Perché? Perché è un sottoinsieme del prodotto cartesiano \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). Ma possiamo ritagliarci ancora di più. Che ne dici di ritagliare un quarto di cerchio? Vedere la regione di seguito.

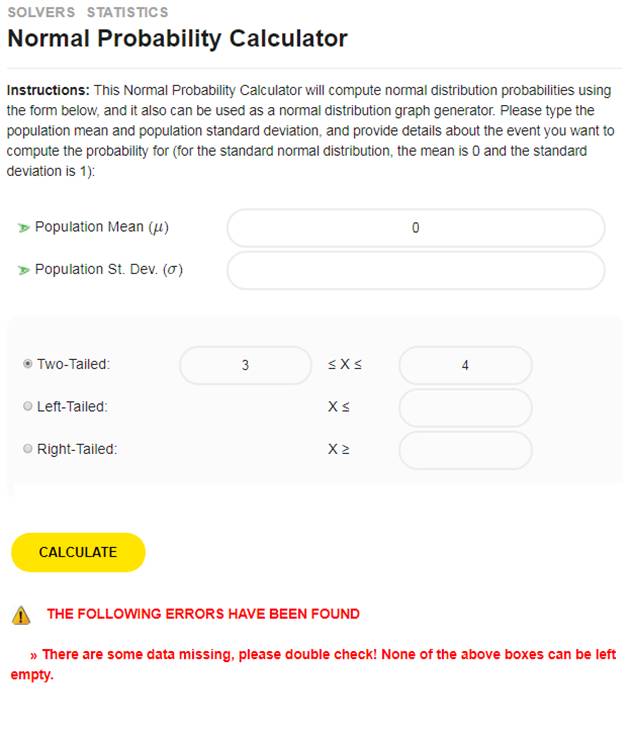
La regione (insieme) sopra è una relazione. Perché? Di nuovo, perché è un sottoinsieme del prodotto cartesiano \(\left[ 0,1 \right]\times \left[ 0,1 \right]\).

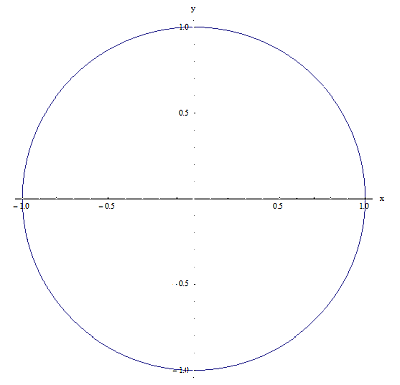
Ora, lascia che ti dia un esempio di due relazioni in \(\left[ -1,1 \right]\times \left[ -1,1 \right]\). Vedi i grafici sotto:

Relazione 1

Relazione 2

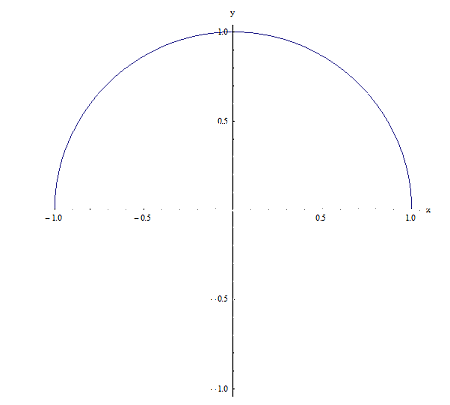
Sono entrambe ovviamente relazioni (perché sono entrambe contenute nel prodotto cartesiano \(\left[ -1,1 \right]\times \left[ -1,1 \right]\), ma hanno una differenza fondamentale: per la relazione 1, per un dato punto x su \(\left[ -1,1 \right]\), ci sono due punti \({{y}_{1}}\) e \({{y}_{2}}\) che hanno la proprietà che \(\left( x,{{y}_{1}} \right)\) e \(\left( x,{{y}_{2}} \right)\) alla relazione 1. Ad esempio per x = 0, ci sono due punti \({{y}_{1}}=1\) e \({{y}_{2}}=-1\) tali che \(\left( 0,1 \right)\) e\(\left( 0,-1 \right)\) appartengono alla relazione 1. Ora, per la relazione 2 non è così perché, ad esempio, per x = 0 è solo \(y=1\) che fa sì che il punto \(\left( 0,1 \right)\) appartenga alla relazione 1.

Infine possiamo definire una funzione: Una funzione \(R\) è un insieme che è una relazione e ha anche la proprietà che se il punto \(\left( x,y \right)\) appartiene a \(R\), allora non c'è altro punto \(\bar{y}\) diverso da \(y\) che ha la proprietà che \(\left( x,\bar{y} \right)\)Z_ A__ anche. In altre parole, una funzione è una relazione con il requisito aggiuntivo che ogni \(x\) nel suo dominio sia associato a un solo \(y\).

Come sapere distinguere tra una funzione e una relazione ??

Gadget! Usiamo un piccolo trucco chiamato "Test della linea verticale": disegniamo una linea verticale immaginaria, e facciamo un giro spostandola da sinistra a destra fino in fondo, e disegnando una mappa mentale di dove la linea verticale interseca la relazione.

• Se in QUALSIASI punto, la linea verticale interseca la relazione in PIÙ di un punto, la relazione fallisce il test della linea verticale e quindi la relazione non è una funzione

• Se in QUALSIASI punto, la linea verticale non interseca la relazione da nessuna parte in PIÙ di un punto, la relazione supera il test della linea verticale e quindi la relazione è una funzione

Guarda i due esempi di seguito:

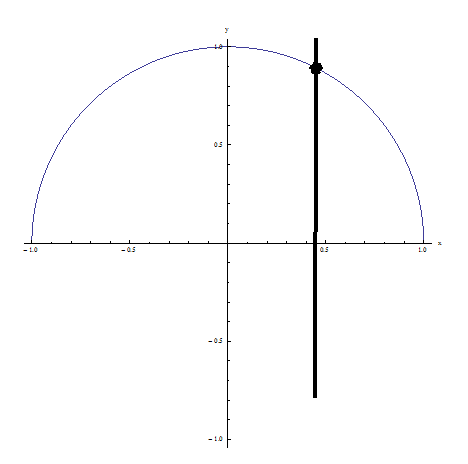
Esempio 1: non supera il test della linea verticale perché la linea verticale mostrata in figura interseca la relazione in più di un punto: NON UNA FUNZIONE

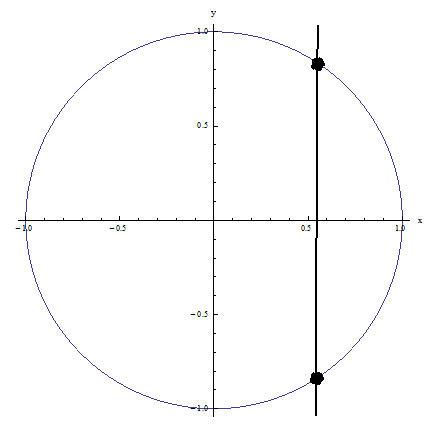
Esempio 2: supera il test della linea verticale perché nessuna linea verticale interseca la relazione in più di un punto: È UNA FUNZIONE!

Esistono molte applicazioni grafiche che possono essere eseguite con funzioni, incluso il calcolo di asintoti orizzontali , asintoti verticali e asintoti inclinati se applicabile.