Ulteriori informazioni sul grafico delle probabilità normali

Un grafico di probabilità normale è un grafico che viene in genere utilizzato per valutare la normalità della distribuzione a cui appartengono i dati campione trasmessi.

Esistono diversi tipi di grafici di normalità (PP, QQ e altre varianti), ma tutti operano sulla stessa base: i quantili teorici di una distribuzione normale standardizzata vengono rappresentati graficamente in relazione ai quantili osservati.

Pertanto, se i dati campione provengono da un popolazione distribuita in modo normale , quindi il grafico della probabilità normale dovrebbe apparire come un 45 ^o linea, con variazioni casuali. Se così non fosse, e il modello del grafico della probabilità normale si discosta in modo significativo/sistematico dal grafico della probabilità normale, allora si dovrebbe sospettare che la distribuzione non sia normale.

Come si calcola un grafico di probabilità normale?

Ci sono diversi passaggi concreti che devi seguire, in un ordine specifico, per costruire un grafico di probabilità normale

1. In questo caso concreto, i dati sono ordinati in ordine crescente e li chiamiamo \(X_1, X_2, ...., X_i , ...., X_n\).
2. Per ogni \(X_i\) in questa sequenza di dati ordinati, calcoliamo le frequenze teoriche \(f_i\), che vengono approssimate utilizzando la seguente formula:
\[ f_i = \frac{i - 0.375}{n + 0.25} \] (where \(i\) corresponds to the position in the ordered dataset)
3. Calcoliamo quindi anche \(z_i\), che corrisponde al punteggio z associato come
\[ z_i = \Phi^{-1}(f_i)\]
4. Quindi, il grafico della probabilità normale si ottiene riportando i valori X ordinati (i dati campione) sull'asse orizzontale e i corrispondenti valori \(z_i\) sull'asse verticale.

Grafico di probabilità normale excel

È possibile tracciare un grafico di probabilità normale in Excel, ma ci vuole un po' di tempo

Calcolatrici per la distribuzione normale e altre

Altri creatori di grafici che puoi utilizzare sono i nostri grafico di distribuzione normale , Creatore di grafici a dispersione o il nostro Creatore di grafici di Pareto .

Esempio: calcolo di un grafico di probabilità normale

Domanda : Ti vengono forniti i seguenti dati campione: 2, 3, 4, 3, 3, 2, 3, 4, 5, 3, 2, 3, 1, 2, 3, 4, 5, 6, 3, 2, 4, 5, 6 10 10 10 12 12 1 2 3 3 e 23. Costruisci un grafico di probabilità normale.

Soluzione:

Dobbiamo costruire un grafico di probabilità normale. Questi sono i dati campione forniti:

Osservazione:	\(X\)
1	2
2	3
3	4
4	3
5	3
6	2
7	3
8	4
9	5
10	3
11	2
12	3
13	1
14	2
15	3
16	4
17	5
18	6
19	3
20	2
21	4
22	5
23	6
24	10
25	10
26	10
27	12
28	12
29	1
30	2
31	3
32	3
33	23

È necessario calcolare le frequenze teoriche \(f_i\) e i punteggi z associati \(z_i\), per \(i = 1, 2, ..., 33\):

Si osservi che le frequenze teoriche \(f_i\) vengono approssimate utilizzando la seguente formula:

\[ f_i = \frac{i - 0.375}{n + 0.25} \]

dove \(i\) corrisponde alla posizione nel set di dati ordinato e \(z_i\) è il punteggio z associato corrispondente. Questo viene calcolato come

\[ z_i = \Phi^{-1}(f_i)\]

Si ottiene la seguente tabella

Posizione (i)	X (Ordine Ascendente)	F io	z io
1	1	0.0188	-2.079
2	1	0.0489	-1.656
3	2	0.0789	-1.412
4	2	0.109	-1.232
5	2	0.1391	-1.084
6	2	0.1692	-0.957
7	2	0.1992	-0.844
8	2	0.2293	-0.741
9	3	0.2594	-0.645
10	3	0.2895	-0.555
11	3	0.3195	-0.469
12	3	0.3496	-0.386
13	3	0.3797	-0.306
14	3	0.4098	-0.228
15	3	0.4398	-0.151
16	3	0.4699	-0.075
17	3	0.5	0
18	3	0.5301	0.075
19	4	0.5602	0.151
20	4	0.5902	0.228
21	4	0.6203	0.306
22	4	0.6504	0.386
23	5	0.6805	0.469
24	5	0.7105	0.555
25	5	0.7406	0.645
26	6	0.7707	0.741
27	6	0.8008	0.844
28	10	0.8308	0.957
29	10	0.8609	1.084
30	10	0.891	1.232
31	12	0.9211	1.412
32	12	0.9511	1.656
33	23	0.9812	2.079

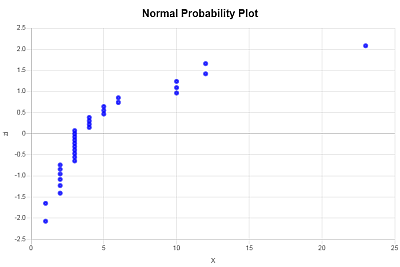
Il grafico di probabilità normale si ottiene tracciando i valori X (i dati del campione) sull'asse orizzontale e i corrispondenti valori \(z_i\) sull'asse verticale. Si ottiene il seguente grafico di normalità: