Ulteriori informazioni su questo calcolatore di probabilità di distribuzione normale per lo strumento di distribuzione campionaria

Quando viene calcolata la media di una sequenza di variabili distribuite normalmente \(X_1, X_2, ...., X_n\), otteniamo la media campionaria

\[\bar X = \frac{1}{n}\sum_{i=1}^n X_i\]

Poiché anche qualsiasi combinazione lineare di variabili normali è normale, anche la media campionaria \(\bar X\) è distribuita normalmente (supponendo che ogni \(X_i\) sia distribuito normalmente). La distribuzione di \(\bar X\) è comunemente indicata come Distribuzione campionaria delle medie campionarie .

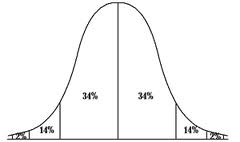
Un altro nome a cui si fa riferimento alla distribuzione normale è la distribuzione gaussiana o la distribuzione a campana.

Come si calcola la distribuzione campionaria?

Supponendo che \(X_i \sim N(\mu, \sigma^2)\), per tutti gli \(i = 1, 2, 3, ...n\), allora \(\bar X\) è normalmente distribuito con la stessa media comune \(\mu\), ma con una varianza di \(\displaystyle\frac{\sigma^2}{n}\).

Questo ci dice che anche \(\bar X\) è centrato su \(\mu \) ma la sua dispersione è minore di quella per ogni singolo \( X_i \). Infatti, maggiore è la dimensione del campione, minore è la dispersione di \(\bar X\).

La formula della distribuzione normale

La formula di distribuzione normale è relativamente difficile, non è quella che gestirai manualmente. La formula è:

\[ f(x)=\frac{1}{\sigma {\sqrt {2\pi }}} e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}\]

La formula della distribuzione normale del campionamento

La chiave quando si lavora con le distribuzioni campionarie è usare il fatto che se \(\mu\) è la media della popolazione e \(\sigma\) è la deviazione standard della popolazione, allora

\[ \displaystyle \frac{\bar X - \mu}{\sigma}\]

ha una distribuzione normale standardizzata. Questo è fondamentale, perché possiamo usarlo per ridurre tutte le distribuzioni campionarie in calcoli di probabilità normali standard .

In termini semplici, quello che stai facendo è ridurre il calcolo di qualsiasi probabilità di distribuzione normale nel calcolo dei punteggi z .

Riducendo tutti i normali calcoli di distribuzione a lavorare con i punteggi z, tutto ciò che devi avere è una tabella normale standard, dove trovare i valori z, o uno strumento come questo calcolatore o Excel.

Qual è la media della distribuzione campionaria

La media delle distribuzioni campionarie, \(\mu(\bar X)\), è uguale alla media sottostante della distribuzione \(\mu\).

Deviazione standard della distribuzione campionaria

A differenza del caso della media, la deviazione standard delle medie campionarie può essere calcolata utilizzando la formula:

\[s(\bar X) = \displaystyle \frac{\sigma}{\sqrt n}\]

Calcolatrici relative alla distribuzione normale

Se vuoi calcolare le probabilità normali per una singola osservazione \(X\), puoi usare questo calcolatore con \(n=1\), oppure puoi usare il nostro normale Calcolatrice della distribuzione normale .

Spesso sei interessato al processo inverso: data una probabilità, vuoi trovare il punteggio come la probabilità a destra di quel punteggio è quella data probabilità, per la quale puoi usare un calcolatrice invnorm

Inoltre, se la visualizzazione grafica è ciò di cui hai bisogno, puoi provare direttamente il nostro creatore di grafici di distribuzione normale .

Inoltre, per valutare se un campione proviene da un'effettiva distribuzione normale, è possibile utilizzare a grafico di probabilità normale , e vedere il modello ottenuto. Se sembra abbastanza lineare, indica che il campione probabilmente proviene da una propulazione normalmente distribuita.

Esempio:

Question : Si consideri una distribuzione normale in cui la media della popolazione è 12 e la deviazione standard della popolazione è 3,4. Supponiamo di prendere campioni di dimensione n = 16. Qual è la probabilità che le medie del campione si trovino nell'intervallo (11,3, 12,4)?

Soluzione:

Di seguito sono riportate la media della popolazione \((\mu)\), la deviazione standard della popolazione \((\sigma)\) e la dimensione del campione \((n)\) fornite:

Population Mean \((\mu)\) =	\(12\)
Population Standard Deviation \((\sigma)\) =	\(3.4\)
Sample Size \((n)\) =	\(16\)
Event to compute its probability =	\(11.3 \leq \bar X \leq 12.4\)

Dobbiamo calcolare \(\Pr(11.3 \leq \bar X \leq 12.4)\). I corrispondenti valori z necessari per essere calcolati sono:

\[Z_{lower} = \frac{X_1 - \mu}{\sigma/\sqrt{n}} = \frac{ 11.3 - 12}{ 3.4/\sqrt{16}} = -0.82 \] \[Z_{upper} = \frac{X_2 - \mu}{\sigma/\sqrt{n}} = \frac{ 12.4 - 12}{ 3.4/\sqrt{16}}= 0.47 \]

Usando le proprietà della distribuzione normale, se \(X ~ N(\mu, \sigma)\), allora le variabili \(Z_{lower} = \displaystyle \frac{X_1 - \mu}{\sigma/\sqrt{n}} \) e \(Z_{upper} = \displaystyle \frac{X_2 - \mu}{\sigma/\sqrt{n}} \) hanno una distribuzione normale standard. Pertanto, la probabilità è calcolata come:

\[ \begin{array}{ccl} \Pr(11.3 \leq \bar X \leq 12.4) & = & \Pr\left(\displaystyle \frac{ 11.3 - 12}{ 3.4 / \sqrt{ 16}} \leq \frac{ \bar X - 12}{ 3.4 / \sqrt{ 16}} \leq \frac{ 12.4 - 12}{ 3.4 / \sqrt{ 16}}\right) \\\\ \\\\ & = & \displaystyle\Pr\left(\frac{ 11.3 - 12}{ 3.4 / \sqrt{ 16}} \leq Z \leq \frac{ 12.4 - 12}{ 3.4 / \sqrt{ 16}}\right) \\\\ \\\\ & = & \displaystyle \Pr\left(-0.82 \leq Z \leq 0.47\right) \\\\ \\\\ & = & \displaystyle \Pr\left(Z \leq 0.47\right) - \Pr\left(Z \leq -0.82\right) \\\\ \\\\ & = & 0.681 - 0.2051 \\\\ \\\\ & = & 0.4759 \end{array}\]

Pertanto, sulla base delle informazioni fornite, si conclude che \( \Pr(11.3 \leq \bar X \leq 12.4) = 0.4759\).