Solveurs Calculus

Règle du produit

Instructions: Utilisez cette calculatrice pour utiliser la règle du produit, pour différencier une fonction donnée, en montrant toutes les étapes. Veuillez saisir la fonction dont vous voulez trouver la dérivée dans le formulaire ci-dessous.

En savoir plus sur la règle du produit

Cette calculatrice vous aidera à trouver la dérivée de fonctions en utilisant la règle du produit. Pour utiliser la calculatrice, vous devez fournir une fonction valide pour laquelle un produit est impliqué.

Un exemple de fonction valide pourrait être quelque chose comme f(x) = x*sin(x), ou quelque chose comme g(x) = sin(x)*cos(x), pour n'en citer que quelques-unes.

Ensuite, on tape la fonction pour laquelle on veut utiliser la règle du produit, il faut ensuite cliquer sur, il suffit de cliquer sur le bouton "Calculer", et toutes les étapes des calculs vous seront fournies.

L'une des premières règles de dérivation que vous apprendrez est en effet la règle du produit, car la plupart des fonctions que vous construisez à partir de fonctions élémentaires utilisent le produit de fonctions.

Formule de la règle du produit

Apprendre à connaître règle de dérivation est peut-être la première chose que vous ferez en apprenant comment trouver la dérivée d'une fonction. Et l'une des premières règles que vous apprendrez est la règle du produit, sans aucun doute.

La règle du produit, en termes simples, est une règle qui vous aide à calculer la dérivée d'un produit de fonctions. La formule de la règle du produit est la suivante :

\[\displaystyle (f(x) g(x))' = f'(x) g(x) + f(x) g'(x) \]

Étapes de l'utilisation de la règle du produit

Étape 1: Identifiez clairement les fonctions f(x) et g(x) qui forment le produit sur lequel vous travaillez
Étape 2: Effectuer des simplifications si nécessaire, tout en conservant la structure du produit
Étape 3: Utiliser la formule de la règle du produit : $(f(x) g(x))' = f'(x) g(x) + f(x) g'(x) $ qui consiste à brancher la valeur des fonctions f(x) et g(x), ainsi que de ses dérivées f'(x) et g'(x)

En travaillant avec la dérivée d'une règle de produit, vous obtenez essentiellement la dérivée du produit sur la base de la connaissance des fonctions individuelles et de leurs dérivées.

Quelles sont les autres règles relatives aux produits dérivés ?

Outre la règle du produit, il existe d'autres règles importantes telles que la règle de la linéarité, la règle de l'égalité des chances et la règle de l'égalité des chances Quotient Rule qui stipule que $\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}$, et la Règle De La Chaîne qui déclare que $\frac{d}{dx} f(g(x)) = f'(g(x))g'(x)$.

Vous trouverez également d'autres règles mentionnées autour, comme la règle de la puissance, qui indique que $\frac{d}{dx} x^n = n x^{n-1}$, pour une constante $n$.

Conseils et astuces

La règle du produit peut être considérée comme une règle de multiplication dérivée, et la règle du produit joue un rôle crucial dans Calculus, il est donc utile de bien l'apprendre.

Notez que dans le cas de fonctions multivariables, vous pouvez utiliser la règle de la multiplication matricielle, afin d'exploiter la règle du produit.

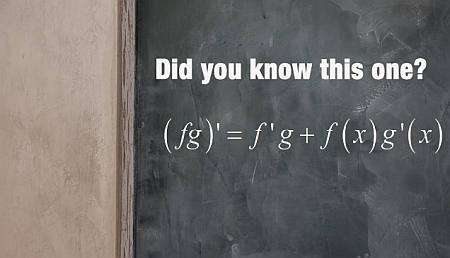
Exemple : utilisation de la règle du produit

Calculez la dérivée de : $f(x) = (x-1)(2x+1) $

Solution: On considère la fonction suivante $\displaystyle f(x)=\left(x-1\right)\left(2x+1\right)$, qui doit être différenciée .

$ \displaystyle \frac{d}{dx}\left(\left(2x+1\right)\left(x-1\right)\right)$

By using the Product Rule: $\frac{d}{dx}\left( \left(2x+1\right)\left(x-1\right) \right) = \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)$

By linearity, we know $\frac{d}{dx}\left( x-1 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)$ and $\frac{d}{dx}\left( 2x+1 \right) = \frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)$, so plugging that in:

$ \displaystyle = \,\,$

$\displaystyle \left(\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\right)$

Since the derivative of a constant is 0, we find that:

$ \displaystyle = \,\,$

$\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)\right)$

It is known that $\frac{d}{dx}\left(x\right) = 1$

$ \displaystyle = \,\,$

$\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right)$

So, we directly get: $\frac{d}{dx}\left( 2x \right) = 2$

$ \displaystyle = \,\,$

$\displaystyle \left(2\right) \left(x-1\right)+\left(2x+1 \right)$

and then we find

$ \displaystyle = \,\,$

$\displaystyle 2x+1+2\left(x-1\right)$

Note that $(2) \cdot (x-1) = 2x-2\cdot 1 = 2x-2$, due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle 2x+1+2x-2$

Grouping the terms with $x$

$ \displaystyle = \,\,$

$\displaystyle \left(2+2\right)x+1-2$

Grouping together numerical values and operating the terms that were grouped with $x$

$ \displaystyle = \,\,$

$\displaystyle 4x+1-2$

Reducing the integers that can be subtracted together: $\displaystyle 1-2 = -1$

$ \displaystyle = \,\,$

$\displaystyle 4x-1$

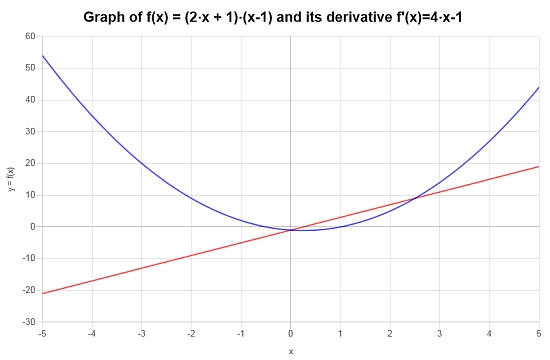
Conclusion : On en conclut donc que la dérivée de la fonction est :

\[f'(x) = 4x-1\]

Graphiquement, le graphique suivant décrit la situation :

Exemples de règles de produits

Trouvez la dérivée de : $f(x) = x \sin(x)$

Solution: Dans cet exemple, la fonction donnée est $\displaystyle f(x)=x\sin\left(x\right)$. Trouvons sa dérivée

$ \displaystyle \frac{d}{dx}\left(x\sin\left(x\right)\right)$

Nous utilisons la règle du produit : $\frac{d}{dx}\left( x\sin\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)$

En différenciant directement, on trouve : $\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \cos\left(x\right)$

Donc après avoir simplifié, on obtient ça :

$ \displaystyle = \,\,$

$\displaystyle x\cos\left(x\right)+\sin\left(x\right)$

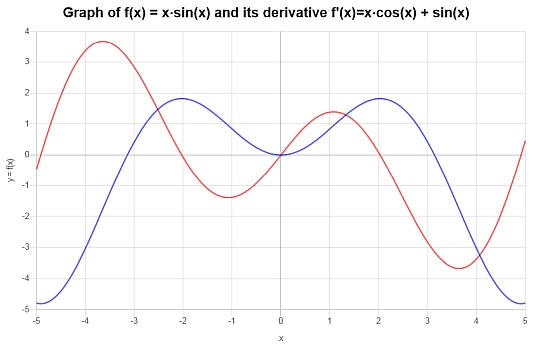
Conclusion : On constate donc que la dérivée est donnée par la formule suivante :

\[f'(x) = x\cos\left(x\right)+\sin\left(x\right)\]

Le graphique suivant est construit pour la fonction et sa dérivée :

Exemple : calcul de la règle d'un autre produit

Différenciez la fonction suivante $ f(x) = x (x+1)^2 $.

Solution: Enfin, pour cet exemple, la fonction donnée est $\displaystyle f(x)=x\left(x+1\right)^2$. Puisqu'il y a un produit de fonction, nous pouvons utiliser la règle du produit pour la différenciation.

$ \displaystyle \frac{d}{dx}\left(\left(x+1\right)^2x\right)$

Nous utilisons la règle du produit : $\frac{d}{dx}\left( \left(x+1\right)^2x \right) = \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)$

Nous savons que $\frac{d}{dx}\left(x\right) = 1$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 $

Utilisation de la règle de la puissance pour un exposant constant : $\frac{d}{dx}\left( \left(x+1\right)^2 \right) = 2x+1\cdot \frac{d}{dx}\left(x+1\right)$

$ \displaystyle = \,\,$

$\displaystyle \left(2x+1\cdot \frac{d}{dx}\left(x+1\right)\right) x+\left(x+1\right)^2 $

Par linéarité, nous connaissons $\frac{d}{dx}\left( x+1 \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)$, donc en branchant ça :

$ \displaystyle = \,\,$

$\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\right)\right) x+\left(x+1\right)^2 $

La dérivée d'une constante est 0, donc.. :

$ \displaystyle = \,\,$

$\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)\right)\right) x+\left(x+1\right)^2 $

Nous savons que $\frac{d}{dx}\left(x\right) = 1$

$ \displaystyle = \,\,$

$\displaystyle \left(2x+1\right) x+\left(x+1\right)^2 $

ce qui conduit alors à

$ \displaystyle = \,\,$

$\displaystyle \left(x+1\right)^2+2\left(x+1\right)x$

Expansion des termes : $\left(x+1\right)^2 = \left(x+1\right)\left(x+1\right)$

$ \displaystyle = \,\,$

$\displaystyle \left(x+1\right)\left(x+1\right)+2\left(x+1\right)x$

Observez que $(x+1) \cdot (x+1) = x^2+1x+1x+1^2 = x^2+2x+1$, comme nous pouvons utiliser la propriété distributive sur chaque terme de l'expression de gauche, par rapport aux termes de droite

$ \displaystyle = \,\,$

$\displaystyle x^2+2x+1+2\left(x+1\right)x$

Notez que $(x+1) \cdot (x) = x^2+1x = x^2+x$, grâce au fait que nous pouvons utiliser la propriété distributive sur chaque terme de l'expression de gauche, par rapport aux termes de droite

$ \displaystyle = \,\,$

$\displaystyle x^2+2x+1+2\left(x^2+x\right)$

On obtient $(2) \cdot (x^2+x) = 2x^2+2x = 2x^2+2x$, en utilisant la propriété distributive sur chaque terme de l'expression de gauche, par rapport aux termes de droite

$ \displaystyle = \,\,$

$\displaystyle x^2+2x+1+2x^2+2x$

Regrouper les termes avec $x$, $x^2$

$ \displaystyle = \,\,$

$\displaystyle \left(2+2\right)x+\left(1+2\right)x^2+1$

Mettre les entiers ensemble et simplifier les termes qui ont été regroupés avec $x$, $x^2$

$ \displaystyle = \,\,$

$\displaystyle 4x+3x^2+1$

On obtient alors

$ \displaystyle = \,\,$

$\displaystyle \left(3x+1\right)\left(x+1\right)$

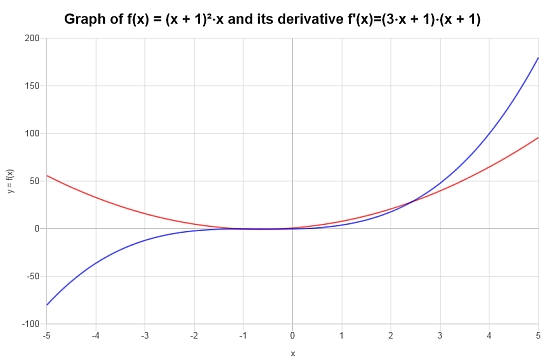
Conclusion : D'après ce qui a été calculé ci-dessus, on constate que la dérivée correspondante est :

\[f'(x) = \left(3x+1\right)\left(x+1\right)\]

On obtient le tracé suivant pour la fonction donnée sur l'intervalle $[-5, 5]$ :

Plus de calculateurs de produits dérivés

Peu de gens seront en désaccord avec le fait que la différenciation, l'intégration et le point central du calcul. Calculer une dérivée est une compétence cruciale que vous devrez apprendre en tant qu'étudiant en calcul.

Vous pouvez apprendre différentes "saveurs" de différenciation, notamment différenciation partielle aussi bien que différenciation implicite qui sont utilisés dans différents contextes d'application.

Les applications comprennent Ligne Tangent qui est identique à un Approximation Linéaire ainsi que l'utilisation de dérivés d'ordre supérieur, à partir de dérivés de second ordre .