La règle du quotient

Cette calculatrice vous permettra d'utiliser la règle du quotient pour une fonction qui implique un quotient, en montrant toutes les étapes du processus. Tout ce que vous devez fournir est une fonction différentiable valide. Cette fonction doit impliquer au moins un quotient pour que la règle du quotient soit applicable.

Un exemple de fonction valide serait f(x) = (x^2 + 2x + 1)/(x^2-1), ou quelque chose comme f(x) = sin(x)/x, etc.

Une fois qu'une fonction valide impliquant des quotients est fournie, vous devez cliquer sur le bouton "Calculer" pour que les étapes du calcul soient affichées.

Avec le Règle Du Produit et Règle De La Chaîne , la Quotient Rule est l'une des bases les plus importantes Règles relatives aux produits dérivés .

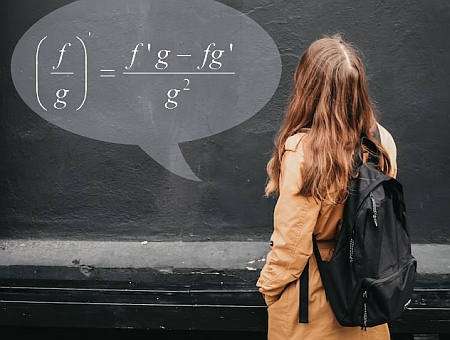
Quotient rule formula

En termes simples, le Quotient Rule vous aide à calculer la dérivée d'un quotient, en utilisant la connaissance des fonctions individuelles et de leurs dérivées. La formule de la règle du quotient est la suivante :

\[\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \]

Quelles sont les étapes à suivre pour utiliser la règle du quotient ?

• Étape 1: Identifiez clairement les fonctions f(x) et g(x) qui entrent dans le numérateur et le dénominateur du quotient
• Étape 2: Simplifier tout terme évident qui peut être simplifié
• Étape 3: Calculez les dérivées correspondantes f'(x) et g'(x)
• Étape 4: Insérez les valeurs trouvées à l'étape 3 dans la formule \(\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \)

Notez que f(x) et g(x) peuvent toujours être des fonctions complexes, et que vous devrez peut-être utiliser d'autres règles, comme la règle de la chaîne, pour calculer à la fois f'(x) et g'(x).

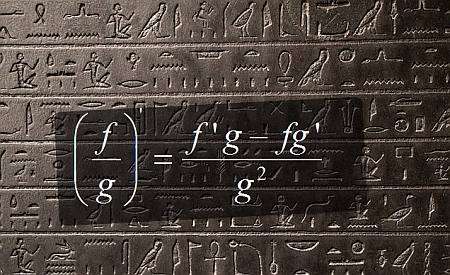
Règle du quotient dérivée

Lorsque vous calculez une dérivée de la règle du quotient, vous réduisez la dérivée d'un quotient à la connaissance des dérivées individuelles, mais ces dérivées individuelles peuvent encore nécessiter de nombreuses étapes avec Règles de base en matière de produits dérivés à résoudre.

C'est pourquoi la différenciation est considérée comme une opération "simple", mais il faut tout de même être suffisamment organisé et garder une trace de tous les morceaux qui apparaissent lors de la décomposition avec les règles de dérivation, puis passer aux plus petits morceaux qui peuvent nécessiter l'application de plus de règles de différenciation.

Vous pouvez donc vous retrouver avec un processus itératif, mais il est garanti qu'il se termine à un moment donné en approfondissant chaque petite partie, jusqu'à ce que vous trouviez une dérivée élémentaire, telle que polynomial ou un dérivée trigonométrique .

Règle du quotient dans la différenciation

Le rôle de la règle du quotient dans la différenciation est assez importante, une bonne raison pour laquelle vous voudrez utiliser une calculatrice pour cela. En termes algébriques, la règle du quotient pourrait être considérée comme plus compliquée que la règle du produit, et cela pourrait être vrai dans de nombreux cas, mais cela dépend en fin de compte de la complexité des fonctions du numérateur et du dénominateur.

Exemples de la règle du quotient

Considérez la fonction : \(f(x) = \frac{x^2+1}{x-2}\), trouvez sa dérivée.

Solution: Pour cet exemple, nous devons analyser la fonction \(\displaystyle f(x)=\frac{x^2+1}{x-2}\), en termes de recherche de sa dérivée.

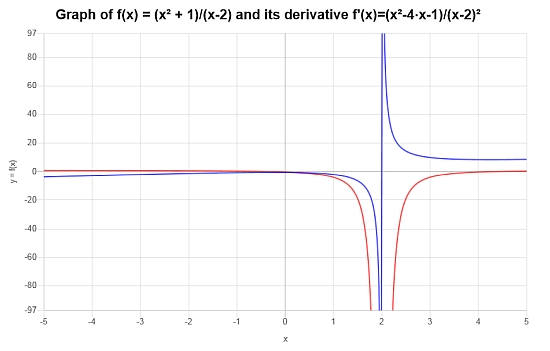
Conclusion : On trouve que la dérivée de la fonction donnée est :

\[f'(x) = \frac{x^2-4x-1}{\left(x-2\right)^2}\]

Ainsi donc, la représentation graphique de la fonction et de sa dérivée est \([-5, 5]\) :

Exemple : calcul de la règle du quotient

Considérons maintenant \(f(x) = \frac{x}{\sin(x)}\), trouvons sa dérivée en utilisant la règle du quotient.

Solution: Pour ce deuxième exemple, la fonction qui nous intéresse est \(\displaystyle f(x)=\frac{x}{\sin\left(x\right)}\). Différencions-la en utilisant la règle du quotient.

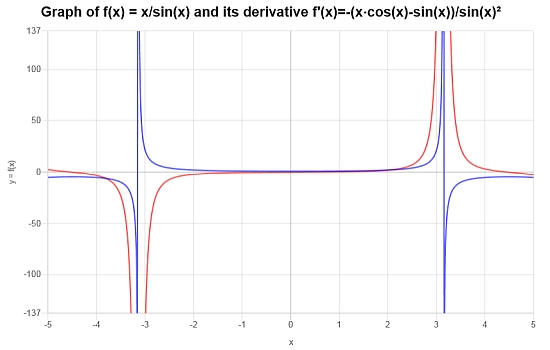
Conclusion : La conclusion est que, d'après le calcul ci-dessus, la dérivée est donnée par :

\[f'(x) = \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\]

Graphiquement, nous pouvons voir la fonction (en bleu) et sa dérivée (en rouge) :

Plus d'exemples de la règle du quotient

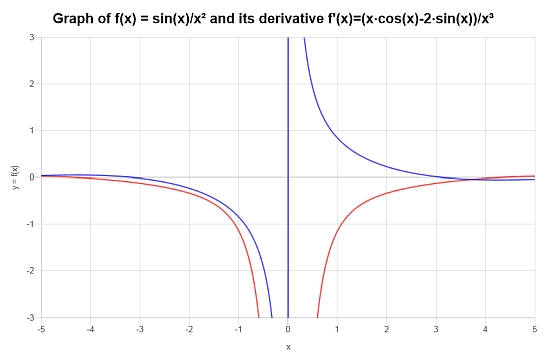
Enfin, considérez la fonction : \(f(x) = \frac{\sin(x)}{x^2}\), trouvez sa dérivée.

Solution: Pour ce dernier exemple de règle du quotient, nous travaillons avec la fonction \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x^2}\). .

Conclusion : Pour la fonction donnée, sa dérivée est :

\[f'(x) = \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\]

Le graphique ci-dessous décrit la situation pour \(f\) et \(f'\) :

Plus de calculateurs de produits dérivés

En calcul, vous allez trouver des dérivés partout où vous regardez. Des milliers d'applications les impliquent, ce qui en fait l'un des outils les plus importants pour la science et l'ingénierie.

Vous devrez vous renseigner sur différenciation implicite pour différentes applications impliquant souvent des taux liés, ou en calcul multivarié vous serez intéressé par trouver des dérivées partielles .

Dans l'ensemble, votre vie sera plus facile en ce qui concerne les produits dérivés si vous êtes en mesure de traiter correctement les questions les plus courantes Règles relatives aux produits dérivés y compris le Règle De La Chaîne ainsi que le Règle Du Produit et Quotient Rule .