Solveurs Calculus

Règles relatives aux produits dérivés

Instructions: Utilisez cette calculatrice de dérivée pour trouver la dérivée de n'importe quelle fonction que vous fournissez, en utilisant les règles de dérivation les plus courantes et en montrant toutes les étapes. Veuillez saisir la fonction à laquelle vous souhaitez appliquer les règles de dérivation dans le champ de formulaire ci-dessous.

A propos des règles dérivées

Cette calculatrice vous permet de calculer la dérivée d'une fonction que vous fournissez en appliquant les règles de différenciation de base requises, en montrant toutes les étapes du processus et en notant où chaque règle est appliquée.

Il vous suffit de fournir une fonction valide et différentiable (ce qui signifie qu'elle a une dérivée). Par exemple, une fonction valide pourrait être f(x) = 1/3*x*sin(x), pour ne citer qu'un exemple.

Ensuite, lorsque vous avez déjà tapé votre fonction, il vous suffit de cliquer sur "Calculer" pour que toutes les étapes de la différenciation soient affichées.

La simplicité des règles relatives aux produits dérivés fait que le processus de différenciation est reconnu comme "facile", un jugement qui est peut-être exagéré.

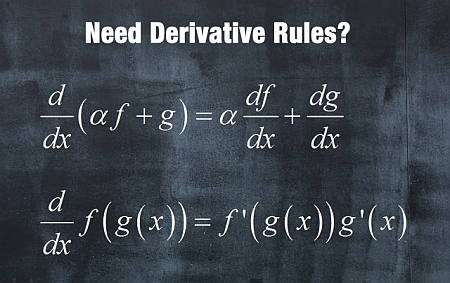
Règles de base en matière de produits dérivés

Vous devez apprendre quatre règles de base en matière de dérivés

Règle De Linéarité : Pour les fonctions $f(x)$ et $g(x)$, et une constante $a$, alors la dérivée est une opération linéaire : $(af(x)+g(x))' = af'(x)+g'(x)$
Règle Du Produit Pour les fonctions $f(x)$ et $g(x)$, la dérivée du produit est $(f(x)g(x))' = f'(x)g(x) + f(x)g'(x)$
Quotient Rule: Pour les fonctions $f(x)$ et $g(x)$, la dérivée du quotient est $\left(\frac{f(x)}{g(x)}\right)' = \left(\frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}\right)$
Règle De La Chaîne Pour les fonctions $f(x)$ et $g(x)$, la dérivée de la fonction composée est $(f(g(x)))' = f'(g(x))g'(x)$

Cette règle fonctionnera comme un charme et vous aidera à trouver la dérivée de n'importe quelle fonction de base.

Comment utiliser les règles relatives aux produits dérivés ?

Étape 1: Identifiez la fonction f(x) que vous voulez différencier, simplifiez si nécessaire
Étape 2: Essayez de décomposer la fonction en petits morceaux dérivés, en utilisant la linéarité
Étape 3: Selon la structure de la fonction f(x), utilisez l'une des règles disponibles (produit, quotient et règle de la chaîne), et sachez que vous devrez peut-être appliquer plusieurs des règles consécutivement)

Habituellement, vous finirez par combiner plusieurs règles de différenciation, jusqu'à ce que vous atteigniez un point où vous trouvez une fonction élémentaire, dont vous savez déjà comment différencier.

Puis-je résoudre tous les dérivés

Dire que l'utilisation des règles de différenciation peut vous amener à résoudre TOUTES les dérivées peut être une exagération. Vous serez capable de résoudre LA PLUPART des dérivées, et certainement toutes les dérivées de base, mais il y a des fonctions qui ont un comportement moins intuitif qui pourraient être définies, bien qu'elles ne soient pas typiquement traitées dans les cours de calcul de base.

Pour ce qui est des fonctions de base, la plupart d'entre elles seront différenciées sans problème.

A règle du produit dérivé , règle du quotient dérivée ou règle de la chaîne dérivée sont peu susceptibles d'être isolées, et se présenteront probablement sous la forme d'une séquence de plusieurs règles qui doivent être utilisées ensemble.

Exemple : règles de dérivation

En utilisant les règles de base des dérivées, calculez la dérivée suivante : $\frac{d}{dx}\left( x^2 \cos(x^2) \right)$

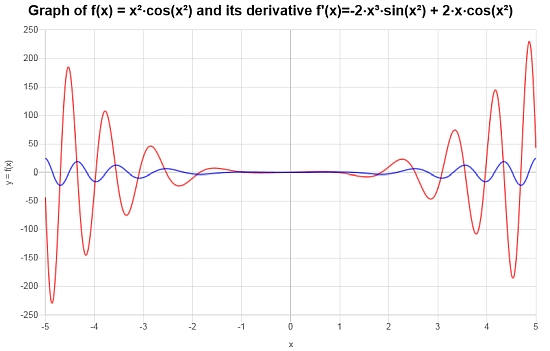
Solution: Considérons la fonction donnée suivante pour laquelle la dérivée doit être calculée $\displaystyle f(x)=x^2\cos\left(x^2\right)$

La fonction n'a pas besoin d'être simplifiée, nous pouvons donc passer directement au calcul de sa dérivée :

$ \displaystyle \frac{d}{dx}\left(x^2\cos\left(x^2\right)\right)$

Now, using the Product Rule: $\frac{d}{dx}\left( x^2\cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)$

We have to use the Chain Rule: $\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)$ and using the Power Rule for polynomial terms: $\frac{d}{dx}\left( x^2 \right) = 2x$

$ \displaystyle = \,\,$

$\displaystyle \left(2x\right) \cos\left(x^2\right)+x^2 \cdot 2x\cdot \left(-\sin\left(x^2\right)\right)$

so then we get

$ \displaystyle = \,\,$

$\displaystyle x^2\cdot 2x\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)$

By reordering some of the numerical values, and then grouping the terms with $x$ in the term $x^2\cdot 2x$

$ \displaystyle = \,\,$

$\displaystyle 2x^3\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)$

But we get $(2x^3) \cdot (-\sin\left(x^2\right)) = -2x^3\sin\left(x^2\right) = -2x^3\sin\left(x^2\right)$, due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle -2x^3\sin\left(x^2\right)+2x\cos\left(x^2\right)$

And finally, grouping the terms together

$ \displaystyle = \,\,$

$\displaystyle -2\left(x^2\sin\left(x^2\right)-\cos\left(x^2\right)\right)x$

Le graphique correspondant de la fonction et de sa dérivée est présenté ci-dessous :

Exemple : plus de règles dérivées

Calculez la dérivée suivante : $\frac{d}{dx}\left( x \cos(x^2+1) \right)$ en utilisant les règles de base des dérivées.

Solution: Maintenant, la tâche à accomplir est de différencier la fonction $\displaystyle f(x)=x\cos\left(x^2+1\right)$

$ \displaystyle \frac{d}{dx}\left(x\cos\left(x^2+1\right)\right)$

In this case, we have to use the Product Rule: $\frac{d}{dx}\left( x\cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)$

The Chain Rule for this composition: $\frac{d}{dx}\left( \cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)$

By linearity, we know $\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)$, so plugging that in:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)$

The derivative of a constant is 0, so then:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)$

Using the Power Rule for polynomial terms: $\frac{d}{dx}\left( x^2 \right) = 2x$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(2x\right)\cdot \left(-\sin\left(x^2+1\right)\right)$

which then leads to

$ \displaystyle = \,\,$

$\displaystyle x\cdot 2x\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)$

Putting together the numerical values and grouping the terms with $x$ in the term $x\cdot 2x$

$ \displaystyle = \,\,$

$\displaystyle 2x^2\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)$

Observe that $(2x^2) \cdot (-\sin\left(x^2+1\right)) = -2x^2\sin\left(x^2+1\right) = -2x^2\sin\left(x^2+1\right)$, due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle -2x^2\sin\left(x^2+1\right)+\cos\left(x^2+1\right)$

So then we get

$ \displaystyle = \,\,$

$\displaystyle -2x^2\cos\left(x^2\right)\sin\left(1\right)-2x^2\cos\left(1\right)\sin\left(x^2\right)+\cos\left(1\right)\cdot \cos\left(x^2\right)-\sin\left(1\right)\cdot \sin\left(x^2\right)$

Exemple de règles de dérivation

Pour la fonction $ f(x) = (x-1)(x^2+1) $, utiliser les règles de dérivation pour trouver sa dérivée.

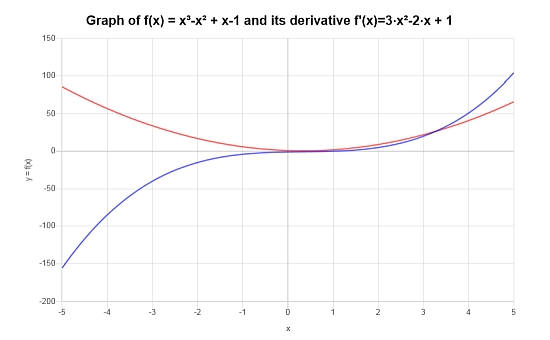
Solution: Pour ce dernier exemple, nous devons différencier : $\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)$.

Étape Initiale : Dans ce cas, nous devons d'abord développer la fonction donnée $\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right) $, et pour ce faire, nous effectuons les étapes de simplification suivantes :

$ \displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)$

Note that $(x-1) \cdot (x^2+1) = x\cdot x^2+x-x^2-1^2 = x^3-x^2+x-1$, due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle x^3-x^2+x-1$

Après avoir développé la fonction, nous pouvons procéder au calcul de la dérivée :

$ \displaystyle \frac{d}{dx}\left(x^3-x^2+x-1\right)$

By linearity, we know $\frac{d}{dx}\left( x^3-x^2+x-1 \right) = \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)$, so plugging that in:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)$

The derivative of a constant is 0, so then:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)$

We know that $\frac{d}{dx}\left(x\right) = 1$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+1$

Using the Power Rule for polynomial terms: $\frac{d}{dx}\left( x^2 \right) = 2x$ and $\frac{d}{dx}\left( x^3 \right) = 3x^2$

$ \displaystyle = \,\,$

$\displaystyle 3x^2-2x+1$

Graphiquement, voici à quoi ressemblent la fonction et sa dérivée :

Plus de calculateurs de produits dérivés

Une des magies de la différenciation est que vous pouvez trouver la dérivée de n'importe quelle fonction en utilisant quelques règles de base simples, dont la Règle Du Produit , Quotient Rule et naturellement, la règle de la chaîne . Ce petit arsenal est généralement suffisant pour calculer n'importe quelle dérivée dont vous avez besoin

La différenciation et l'intégration sont les voies principales du Calcul, sans conteste, car elles sont au centre de tant d'applications, dans tous les aspects de la science. Des taux relatifs aux différenciation implicite avec dérivés partiels en physique et en économie