A propos de cette calculatrice de ligne de tangente

Cette calculatrice vous permettra d'effectuer de manière transparente les calculs nécessaires pour obtenir la ligne tangente d'une fonction, en un point donné, en montrant toutes les étapes.

Tout ce que vous devez faire est de fournir une fonction valide f(x), et un point où vous voulez la ligne tangente. La fonction peut être n'importe quelle fonction valide et différentiable comme f(x) = sin(x), ou f(x) = x^2 - x + 1, etc. Le point peut être n'importe quelle expression numérique valide, comme 1/2 par exemple.

Ensuite, lorsque les informations requises ont été fournies, et qu'elles sont valides, vous devez cliquer sur "Calculer" pour que toutes les étapes de l'équation de la ligne tangente vous soient montrées.

Les applications de la ligne tangente abondent dans le domaine scientifique. Également appelé premier ordre ou approximation linéaire si l'expression a un sens très profond en physique et en ingénierie, où l'idée de la principale contribution au changement (la partie de premier ordre) est celle qui dévoile beaucoup d'informations sur un processus.

Quelle est la ligne tangente

En termes simples, une ligne tangente est une ligne qui coupe une courbe, mais en un seul point (au moins localement). Cette ligne tangente est construite en fixant un point \(x_0\) et en prenant un autre point \(x_1\).

Ensuite, en construisant la ligne qui passe par les points \((x_0, f(x_0))\) et \((x_1, f(x_1))\), nous obtenons ce que l'on appelle une Secant Line comme le montre le graphique ci-dessous :

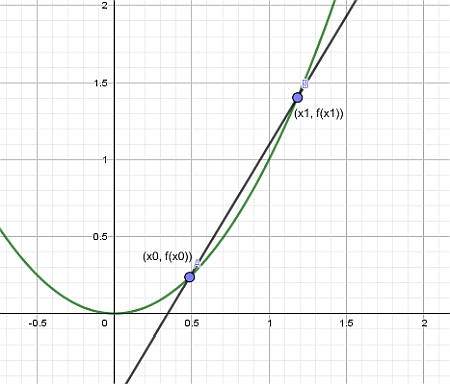
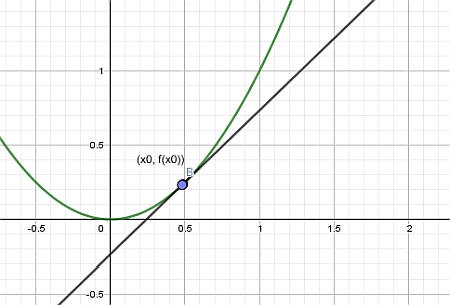
Enfin, nous laissons le point \(x_1\) s'approcher de \(x_0\), et nous obtenons la ligne tangente :

Étapes pour trouver la ligne tangente de manière géométrique

• Étape 1 : Identifiez la fonction f(x) avec laquelle vous voulez travailler, ainsi que le point x0. Vous avez besoin de ces deux éléments
• Étape 2 : Le point (x0, f(x0)) sera sur la courbe de la fonction f(x). Tracez-le
• Étape 3 : Choisissez un point (x1, f(x1)), pour un x1 qui est différent de x0 (peut être à gauche ou à droite de x). Tracez-le
• Étape 4 : Tracez une ligne passant par les points (x0, f(x0)) et (x1, f(x1))
• Étape 5 : Choisissez un point x2 qui est à mi-chemin entre x0 et x1, et tracez une ligne passant par les points (x0, f(x0)) et (x2, f(x2))
• Étape 6 : Répétez ce processus plusieurs fois

Cette méthode graphique vous aidera à avoir une idée approximative de l'aspect de la ligne tangente, mais il s'agit d'une approximation (sauf si la fonction f(x) est linéaire).

Formule de la ligne tangent

La méthode d'approximation utilisant les droites sécantes peut vous donner une idée de ce que vous recherchez, mais heureusement, il existe une formule exacte pour calculer la droite tangente à une fonction en un point \(x_0\). La formule de la ligne tangente est la suivante :

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

Simple, hein ? En termes simples, cette formule nous dit que la ligne tangente est une ligne qui passe par le point \((x_0, f(x_0))\) et qui a une pente de \(m = f'(x_0)\)

Ainsi, en termes simples, la pente de la ligne tangente en un point donné est exactement la dérivée de la fonction en ce point.

Étapes de l'application de la formule de la ligne tangente

• Étape 1 : Identifier la fonction f(x) et le point x0
• Étape 2 : Calculer la valeur de la fonction en x0, qui est f(x0)
• Étape 3 : Calculez la dérivée de f(x) au point x0, vous avez donc besoin de f'(x0)
• Étape 4 : Appliquer directement la formule de la ligne tangente \(y = f(x_0) + f'(x_0) (x - x_0)\)

Une fois que vous avez le équation de la droite vous pouvez le transformer dans le format le plus utile pour la situation en question.

La pente de la ligne tangente

L'une des principales conclusions est que la pente de la ligne tangente au point \(x_0\) est exactement \(f'(x_0)\), qui est la dérivée au point \(x_0\). Cela donne une interprétation claire et extrêmement utile de la dérivée en termes géométriques.

Cette connexion permet de trouver l'équation de la ligne tangente à une courbe donnée en un point donné en regardant simplement la dérivée de la fonction.

Quand a-t-on une ligne tangente horizontale ?

Une ligne tangente horizontale apparaît lorsque le point choisi \(x_0\) lorsque la dérivée correspondante en ce point est égale à zéro. Dans ce cas, la ligne tangente (qui est la ligne qui touche localement la courbe en un point) sera parallèle à l'axe des y.

Ainsi, tout ce que vous devez savoir pour identifier les lignes tangentes horizontales est de trouver les points où la dérivée de la fonction est nulle.

Quand a-t-on une ligne tangente verticale ?

Une ligne tangente verticale apparaît lorsque la dérivée est "infinie" en un point. C'est une façon simple de dire que la dérivée n'est pas définie en un point donné, mais qu'elle converge vers l'infini au fur et à mesure que l'on s'approche du point.

Par exemple, on pourrait dire que \(f(x) = \frac{1}{x}\) a une ligne tangente verticale à x = 0. Cependant, on pourrait dire qu'il n'y a pas de ligne tangente parce que la dérivée n'est pas bien définie à x = 0.

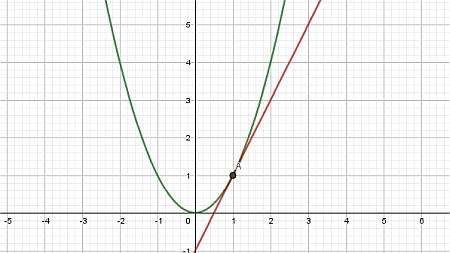
Exemple : ligne tangente

Trouver l'équation de la droite tangente à \(f(x) = x^2 - 2x + 1\), au point \(x_0 = 2\).

Solution : La fonction suivante est celle avec laquelle nous devons travailler : \(\displaystyle f(x)=x^2-2x+1\). Tout d'abord, nous devons calculer sa dérivée.

La fonction est déjà simplifiée, nous pouvons donc procéder directement au calcul de sa dérivée :

Ligne Tangent : L'équation de la droite tangente à la fonction \(\displaystyle f(x)=x^2-2x+1\) au point \(x_0 = 2\) est :

\[y = y_0 + f'(x_0)(x - x_0) \]

Dans ce cas, \(\displaystyle y_0 = f(x_0)\), donc en introduisant la valeur du point \(x_0 = 2\) dans la fonction, on obtient :

\[y_0 = f(x_0) = f(2) = 2^2-2\cdot 2+1 = 1 \]

De même, l'insertion de la valeur du point \(x_0 = 2\) dans la dérivée calculée conduit à :

\[f'(x_0) = f'(2) = 2\cdot 2-2 = 2 \]

Donc, on introduit ces valeurs dans la formule de la ligne tangente pour obtenir.. :

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 1+2\left(x-2\right) = 2x-3 \]

Conclusion : On trouve donc que la droite tangente à la fonction \(\displaystyle f(x)=x^2-2x+1\) au point \(x_0 = 2\) est :

\[y = 2x-3 \]

Le graphique suivant est obtenu pour la fonction donnée et sa ligne tangente à \(x_0 = 2\) :

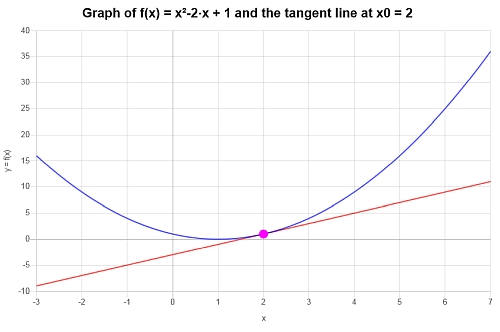
Exemple : équation de la ligne tangente

Quelle est la ligne tangente à x = 1/2, pour la fonction \(f(x) = \sin(x) + 1\) ?

Solution :

La fonction suivante a été fournie : \(\displaystyle f(x)=\sin\left(x\right)+1\), pour laquelle nous devons calculer sa dérivée.

La fonction est déjà simplifiée, nous pouvons donc procéder directement au calcul de sa dérivée :

Ligne Tangent : L'équation correspondante de la droite tangente au point \(x_0 = \frac{1}{2}\) est donnée par :

\[y = y_0 + f'(x_0)(x - x_0) \]

Mais dans ce cas précis, \(\displaystyle y_0 = f(x_0)\), ce qui signifie que nous devons introduire la valeur du point \(x_0 = \frac{1}{2}\) dans la fonction, ce qui nous permet d'obtenir :

\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \sin\left(\frac{1}{2}\right)+1\]

Maintenant, en faisant la même chose au niveau de la dérivée, pour \(x_0 = \frac{1}{2}\) nous trouvons

\[f'(x_0) = f'\left(\frac{1}{2}\right) = \cos\left(\frac{1}{2}\right) \]

Maintenant, nous avons juste besoin de brancher les valeurs, donc nous trouvons que

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = \sin\left(\frac{1}{2}\right)+1+\cos\left(\frac{1}{2}\right)\left(x-\frac{1}{2}\right) = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

Conclusion : Nous trouvons que la ligne tangente correspondante que nous cherchons, au point correspondant \(x_0 = \frac{1}{2}\) est donnée par

\[y = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

Graphiquement :

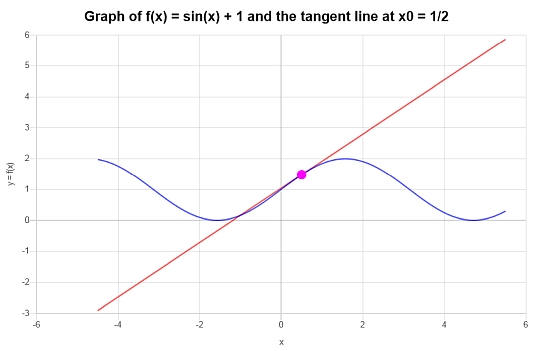
Exemple : une autre ligne tangente

Quelle est la ligne tangente à x = 0, pour la fonction \(f(x) = \cos(x)\) ? Ce résultat a-t-il un sens ?

Solution : Observez que \(f'(x) = -\sin(x)\), donc \(f'(0) = -\sin(0) = 0\). En d'autres termes, la ligne tangente a une pente de m = 0 à x = 0, donc l'équation de la ligne tangente est simplement \(y = y_0 = \cos(0) = 1\). Ceci est logique car dans ce cas, la ligne tangente est une ligne horizontale.

Plus de calculateurs de différenciation

Certaines personnes peuvent prétendre que la différenciation est un exercice relativement simple, et que l'utilisation d'un outil d'analyse de l'environnement est une bonne chose calculatrice de dérivées peut ne pas être nécessaire, mais en réalité, le calcul des dérivés peut toujours être assez lourd et nécessiter de longues heures de travail calculs algébriques .

Lorsque vous avez une expression avec plus d'une variable, afin de trouver la dérivée, vous devez déterminer si les variables sont indépendantes les unes des autres, dans ce cas vous utilisez dérivés partiels ou s'il y a une équation qui lie les variables, auquel cas il faut utiliser différenciation implicite .

Les deux principaux domaines du calcul différentiel sont l'intégration et la différentiation, et ils ont tous deux leurs vastes applications, partout. dérivés partiels apparaissent en détail dans les applications d'ingénierie et d'économie.

D'une part, la différenciation traite de taux de changement infinitésimaux, alors que l'intégration traite de la somme de taux de changement infinitésimaux, et admirablement bien, ils sont étroitement liés par l'intégration Théorème fondamental du calcul .