Différenciation implicite

Cette calculatrice vous aidera à effectuer la différentiation implicite d'une équation qui implique les variables x et y. Vous devez fournir une équation valide comme x^2 + y^2 = 1, ou xy - x^2 y^2 = 0, etc.

Une fois que vous avez fourni une équation valide impliquant deux variables (\(x\) et \(y\)), il vous suffit de cliquer sur le bouton "Calculer", et toutes les étapes de la différenciation implicite correspondante seront affichées.

Il s'agit d'un calculatrice dy/dx avec étapes en ce sens qu'il vous montrera toutes les étapes pertinentes du calcul de la dérivée d'une variable par rapport à une autre, pour autant que ces deux variables soient liées dans une équation. C'est cette relation qui vous permet de trouver la dérivée correspondante dérivée implicite .

L'existence d'une équation reliant les deux variables \(x\) et \(y\) nous indique que nous devrions être en mesure d'exprimer \(y\) en tant que fonction de \(x\) et d'écrire \(y = y(x)\). Souvent, nous ne pouvons pas exprimer explicitement \(y\) en tant que fonction de \(x\) - nous supposons qu'une telle fonction existe, auquel cas, il est logique de différencier \(y\) par rapport à \(x\).

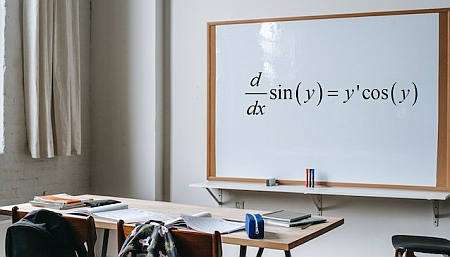
Qu'est-ce que la différenciation implicite ?

La différenciation implicite est une calcul de différenciation est basée sur l'hypothèse qu'il est possible d'affirmer, à partir d'une équation donnée impliquant \(x\) et \(y\), que \(y\) est une fonction de \(x\), bien qu'il soit souvent impossible d'écrire explicitement une telle fonction.

Une fois cette hypothèse posée, nous supposons que nous pouvons calculer \(\frac{dy}{dx}\) et que nous pouvons utiliser toutes les données connues de l Règles relatives aux produits dérivés ( Règle Du Produit , Quotient Rule et Règle De La Chaîne ) pour différencier les deux côtés de l'équation et résoudre \(\frac{dy}{dx}\).

Qu'est-ce que la méthode de différenciation implicite ?

La méthode de différenciation implicite est une méthode qui permet de calculer une dérivée pour des expressions qui ne sont pas directement mises au format \(f(x)\). En d'autres termes, lorsqu'une fonction d'une variable \(x\) est donnée, par exemple, il suffit d'aller de l'avant et de différencier cette fonction.

Mais lorsque deux variables \(x\) et \(y\) sont reliées par une équation, comme \(x^2+y^2 = 1\) par exemple, vous pouvez également différencier y par rapport à x. Selon la méthode traditionnelle, vous devez résoudre y en termes de x, et ensuite vous pouvez différencier.

En utilisant la différenciation implicite, vous pouvez différencier directement, en faisant seulement l'hypothèse que \(y = y(x\), et en utilisant la fonction de différenciation implicite Règle De La Chaîne .

Étapes de l'utilisation de la différenciation implicite

• Étape 1 : Identifiez l'équation qui implique deux variables x et y. Simplifiez les termes redondants
• Étape 2 : Supposons que y soit une fonction de x, y = y(x), il est donc logique de calculer la dérivée de y par rapport à x
• Étape 3 : Calculer la dérivée des deux côtés de l'équation en utilisant tous les Règles relatives aux produits dérivés dont vous avez besoin. Cela conduira à une égalité dans laquelle x, y et y' sont présents potentiellement
• Étape 4 : Résolvez ce que vous avez obtenu à l'étape 3 pour y'. Notez que y' sera généralement écrit comme une fonction de x et de y, ce qui est bien, puisque y dépend aussi de x

Il s'agit d'une méthodologie très générale, qui présentera des subtilités d'un cas à l'autre, mais c'est le schéma directeur qui devrait fonctionner dans la plupart des cas, avec la difficulté potentielle supplémentaire des manipulations algébriques.

Pourquoi utiliser une calculatrice de différentiation implicite

La différenciation implicite peut parfois prêter à confusion, si vous ne savez pas très bien ce que vous différenciez, et par rapport à quelle variable. Une calculatrice vous aidera à comparer vos résultats et l'une des particularités de notre calculatrice est que toutes les étapes du processus sont indiquées.

C'est une aide cruciale pour vous, car elle vous montrera exactement quelle règle de dérivation, et où vous l'avez appliquée.

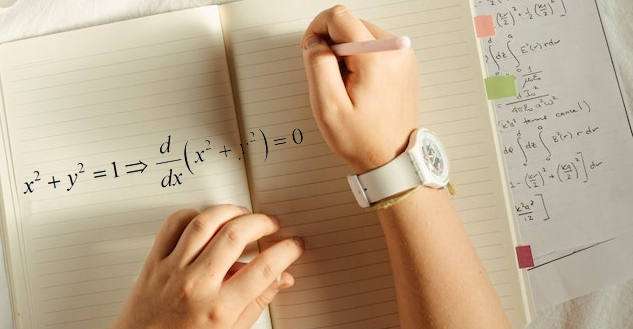
Quel est l'intérêt d'une différenciation implicite ?

C'est une question pertinente. Si vous avez une équation impliquant x et y, pourquoi ne pas résoudre y en fonction de x et utiliser le calcul de la dérivée ordinaire pour obtenir la dérivée de y par rapport à x. Je peux vous donner au moins deux bonnes raisons :

• Raison 1 : Il se peut que vous ne puissiez pas résoudre y en fonction de x de manière explicite. Il peut y avoir une fonction, mais vous ne pouvez pas simplement la trouver. Pensez à y + tan(y) = x^2
• Raison 2 : Même si vous vous trouvez résoudre y en fonction de x si le calcul de la dérivée implicite n'est pas possible, il peut s'agir d'une expression très compliquée, et le calcul de la dérivée peut être très compliqué et difficile. Habituellement, la différenciation implicite est algébriquement simple, en termes relatifs

La dérivée implicite dépend-elle de y ?

Pas toujours, mais souvent. Cela ne fait que dire que \(\frac{dy}{dx}\) peut dépendre de x et de y, mais comme y dépend de x, cela revient à dire que, comme prévu, \(\frac{dy}{dx}\) dépend de x.

Différents exemples de différenciation implicite seront présentés dans la section suivante.

Dérivée implicite seconde

Une question se pose : peut-on calculer la dérivée seconde à l'aide de la différenciation implicite ? La réponse est OUI. Il suffit de faire la même chose qu'avec la dérivée première en utilisant la différenciation implicite, vous supposez simplement que \(y\) est une fonction de \(x\), donc vous écrivez \(y = y(x)\), et vous pouvez différencier autant que vous le souhaitez.

Par exemple, disons que vous voulez trouver \(\frac{d^2y}{dx^2}\) étant donné l'équation \(x^2+y^2=1\). Différencier les deux côtés par rapport à \(x\) :

\[ \frac{d}{dx}\left(x^2+y^2\right)=\frac{d}{dx}\left(1\right)\] \[ \Rightarrow 2x+2yy' = 0\]

Il faut maintenant différencier à nouveau par rapport à x :

\[ \frac{d}{dx}\left(2x+2yy'\right)=\frac{d}{dx}\left(0\right)\] \[ \Rightarrow 2+2(y')^2+2yy'' = 0\]

et maintenant nous résolvons \(y''\) :

\[ \Rightarrow y'' = -\frac{(2+2(y')^2)}{2y}\] \[ \Rightarrow y'' = -\frac{(1+(y')^2)}{y}\]

Exemple : exemple de différenciation implicite

Trouvez \(\frac{dy}{dx}\) pour l'équation : \(x^2 - y^2 = 2y\)

Solution : Il s'agit d'un exemple de différenciation implicite. L'équation suivante a été fournie : \(\displaystyle x^2-y^2=2y\), pour laquelle nous devons effectuer une différenciation implicite, où nous supposons que \(y\) est une fonction de \(x\) .

L'équation ne nécessite pas de simplification supplémentaire, nous pouvons donc procéder à la différenciation implicite :

Nous devons différencier les deux côtés de l'équation par rapport à \(x\), et nous supposons que \(y = y(x)\).

Côté gauche : Différenciation du côté gauche par rapport à \(x\)

Côté droit : Différenciation du côté droit par rapport à \(x\)

Par conséquent, après avoir différencié les deux côtés par rapport à \(x\), on obtient ce qui suit :

\[\displaystyle 2x-2y\frac{dy}{dx} = 2\frac{dy}{dx}\]

Mettre tous les termes d'un côté :

\[-2\,y\frac{d}{dx}y+2\,x-2\,\frac{d}{dx}y = 0\]

Regroupement de tout ce qui contient \(\displaystyle \frac{dy}{dx}\) :

\[-2\,{\left(y+1\right)}\frac{d}{dx}y+2\,x = 0\]

Enfin, la résolution de \(\displaystyle \frac{dy}{dx}\) conduit à :

\[\displaystyle \frac{dy}{dx} = \frac{x}{y+1}\]

Exemple : plus de calculs de différenciation implicite

Quelle est la pente de la ligne tangente au cercle unitaire au point \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\) ?

Solution : Remarquez que l'équation du cercle unitaire est \(\displaystyle x^2 + y^2 = 1\), ce qui définit implicitement \(y\) comme une fonction de \(x\). Pour trouver la ligne tangente, nous devons calculer \(\frac{dy}{dx}\) au point spécifié. En utilisant la différenciation implicite, nous différencions les deux côtés de l'équation qui définit le cercle unitaire : \[\displaystyle x^2 + y^2 = 1\] \[\Rightarrow \displaystyle \frac{d}{dx}\left(x^2 + y^2\right) = \frac{d}{dx}\left(1\right)\] \[\Rightarrow \displaystyle 2x+2yy' = 0 \] \[\Rightarrow \displaystyle 2yy' = -2x \] \[\Rightarrow \displaystyle y' = -\frac{x}{y} \]

Le point d'intérêt est \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\), donc .

\[\displaystyle y' \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) = -\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = -1\]

Ceci implique que la pente de la droite tangente au point \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\) est \(m = -1\), ce qui implique que l'équation de la droite tangente en ce point est

\[\displaystyle y - \frac{\sqrt{2}}{2} = -\left(x-\frac{\sqrt{2}}{2}\right)\] \[\Rightarrow \displaystyle y = \frac{\sqrt{2}}{2} - x + \frac{\sqrt{2}}{2}\] \[\Rightarrow \displaystyle y = \sqrt{2} - x \]

Exemple de différenciation implicite

Considérons l'équation : \( \displaystyle \frac{2}{3} x + y^2 = \frac{2}{5} \). Calculer \(\frac{dy}{dx}\)

Solution : Dans ce cas, nous avons l'équation suivante : \(\displaystyle \frac{2}{3} x + y^2 = \frac{2}{5}\), nous devons donc procéder à une différenciation implicite, en supposant que \(y\) dépend de\(x\) .

Une simplification supplémentaire de l'équation n'est pas nécessaire, ce qui nous permet de procéder à la différenciation implicite :

Nous devons maintenant calculer la dérivée des deux côtés par rapport à la variable \(x\), en supposant que \(y = y(x)\).

Côté gauche : Différenciation du côté gauche par rapport à la variable \(x\)

Côté droit : Nous différencions maintenant le côté droit par rapport à \(x\)

Par conséquent, le résultat obtenu après avoir différencié les deux côtés par rapport à \(x\) est :

\[\displaystyle \frac{2}{3}+2y\frac{dy}{dx} = 0\]

Par conséquent, nous pouvons maintenant résoudre \(\displaystyle \frac{dy}{dx}\) pour obtenir :

\[\displaystyle \frac{dy}{dx} = -\frac{1}{3\,y}\]

Autres solveurs de calcul utiles

L'une des applications les plus intéressantes de la Règles relatives aux produits dérivés est le concept de différenciation implicite. Il a des applications en physique, en économie et en ingénierie, et il est extrêmement pratique pour décrire le taux de variation le long de courbes.

Un autre type de produits dérivés est dérivés partiels dans lequel, contrairement au cas de la différenciation implicite où nous supposons que y = y(x), dans ce cas, y est considéré comme une constante lorsque x change.