Calculateur de période et de fréquence

Lorsque l'on traite des fonctions périodiques, il y a quelques paramètres cruciaux qui doivent être calculés, et ce sont la période (\(P\)) et la fréquence (\(f\)).

La période \(P\) d'une fonction périodique correspond au nombre qui satisfait à la propriété suivante :

\[f(x+P) = f(x)\]

pour toutes les valeurs de \(x\). Observez que toutes les fonctions ne comportent pas de point. Celles qui en ont un sont appelées fonctions périodiques .

Période de quelques fonctions courantes

Les fonctions trigonométriques sont des exemples de fonctions périodiques. Par exemple, si on considère la fonction, \(f(x) = \sin x\), sa période est \(2\pi\), comme le montre le graphique ci-dessous :

Pour \(\cos x\), nous avons également la période \(2\pi\). Regardez le graphique ci-dessous :

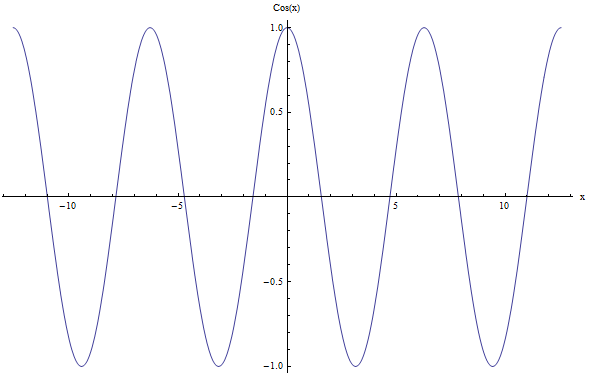
Période d'autres fonctions trigonométriques

Rappelons que la fonction cosécante \(\csc x\) est l'inverse de \(\sin x\), c'est \(\csc x = \frac{1}{\sin x}\), donc alors la période de \(\csc x\) est aussi \(2\pi\).

De même, la fonction sécante \(\sec x\) est l'inverse de \(\cos x\), c'est \(\sec x = \frac{1}{\cos x}\), donc alors la période de \(\sec x\) est \(2\pi\) également.

Et la tangente ? La fonction tangente \(\tan x\) est légèrement différente car sa période est \(\pi\). En effet, son graphe semble différent de ceux du sinus et du cosinus, mais la tangente est également périodique. Une différence est que \(\tan x\) a des discontinuités. Vérifiez-le :

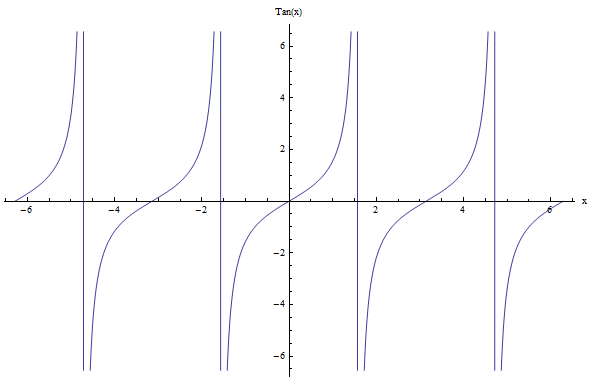
De même que précédemment, la fonction cotangente \(\cot x\) est l'inverse de \(\tan x\), avec \(\cot x = \frac{1}{\tan x}\), donc alors la période de \(\cot x\) est aussi \(\pi\).

Calcul de la fréquence

Un autre élément important à considérer pour la fonction périodique est la fréquence (\(f\)), qui est calculée en fonction de la période \(P\) comme :

\[f = \frac{1}{P}\]

La fréquence est donc l'inverse de la période. Et vice-versa, la période est l'inverse de la fréquence.

Par exemple, quelle est la fréquence de \(\sin x\) ? En suivant la formule ci-dessus, puisque nous savons que pour le sinus la période est \(P = 2\pi\) :

\[f = \frac{1}{P} = \frac{1}{2\pi} \approx 0.1592\]

Cette calculatrice calculera également l'amplitude, le déphasage et le décalage vertical si la fonction est correctement définie. Ces paramètres déterminent en grande partie le comportement de la fonction trigonométrique.

Si vous devez tracer le graphique d'une fonction trigonométrique, vous devez utiliser ceci créateur de graphiques trigonométriques .