Résolveurs Calculus

Calculateur d'approximation linéaire

Instructions : Utilisez cette calculatrice pour calculer l'approximation linéaire d'une fonction donnée à un point donné que vous fournissez, en montrant toutes les étapes. Veuillez saisir la fonction et le point dans le formulaire ci-dessous.

Calculateur d'approximation linéaire

Le Présent calculateur de linéarisation permettra de calculer l'approximation linéaire, également connue sous le nom de Ligne Tangent pour toute fonction valide donnée, à un point valide donné.

Vous devez fournir une fonction valide comme par exemple f(x) = x*sin(x), ou f(x) = x^2 - 2x + 1, ou toute autre fonction valide qui est différentiable, et un point $x_0$ où la fonction est bien définie. Ce point peut être n'importe quelle expression numérique valide, comme 1/3, par exemple.

Une fois que vous avez fourni une fonction et un point valides, vous cliquez sur "Calculer" et tous les calculs s'affichent pour vous.

L'approximation linéaire ou de premier ordre recherche une approximation de la fonction donnée par une droite, en un point donné $x_0$. Naturellement, pour les courbes, une approximation linéaire sera approximative, mais l'idée principale est que l'approximation sera précise pour les points proches de $x_0$.

Approximation linéaire

L'idée est de trouver une ligne qui passe par le point $(x_0, f(x_0))$ et qui "touche à peine" la fonction $f(x)$. La définition mathématique formelle de "toucher à peine" est donnée par l'idée de Ligne Tangent pour lequel nous devons Calculer la dérivée de la fonction.

En fait, la formule de l'approximation linéaire au point $x_0$ dépend de la dérivée $f'(x_0)$, comme suit

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

Le Présent formule d'approximation linéaire définit essentiellement le équation d'une droite qui passe par le point $(x_0, f(x_0))$, c'est pourquoi on l'appelle "approximation linéaire", car elle définit une fonction linéaire qui coïncide avec $f(x)$ au point $x_0$, et elle est très proche de $f(x)$ pour des valeurs de $x$ qui sont proches de $x_0$.

Étapes pour trouver l'approximation linéaire

Étape 1 : Vous devez avoir une fonction donnée f(x) et un point x0. La fonction doit être différentiable en x0
Étape 2 : Calculer f(x0) et f'(x0), qui sont la fonction et la dérivée de la fonction f au point x0
Étape 3 : Définir l'approximation linéaire comme y = f(x_0) + f'(x_0) (x - x_0), ce qui correspond à la formule de linéarisation présentée ci-dessus

Cette ligne, $y = f(x_0) + f'(x_0) (x - x_0)$, représente l'approximation de premier ordre, également connue sous le nom d'approximation linéaire locale.

Lien avec la ligne tangente

Comme vous l'avez probablement soupçonné jusqu'à présent, l'approximation linéaire est la même que celle de l'approximation linéaire Ligne Tangent au point donné. Ensuite, le calcul de l'approximation linéaire est exactement le même que le calcul de la ligne tangente

On parle également d'approximation du premier ordre ou d'approximation de la ligne tangente, qui sont également des noms couramment utilisés en calcul.

Approximation différentielle et linéaire

Un autre concept commun est celui de différentielle, qui est étroitement lié à celui de l'approximation linéaire, et qui en est simplement une dérivation. En effet, la différentielle (ou différence finie) est définie comme $\Delta y = y - f(x_0)$. Ainsi, en se basant sur la formule d'approximation du premier ordre, la formule de la différentielle est la suivante

\[\displaystyle \Delta y = y - f(x_0) = f'(x_0) (x - x_0) = f'(x_0) \Delta x \]

Cette formule ressemble naturellement à la formule d'approximation linéaire, sauf que le terme $f(x_0$ est passé à gauche.

Exemple : calcul de l'approximation du premier ordre.

Considérez ce qui suit : $f(x) = x^2 - 2x + 3$, trouvez son approximation du premier ordre à $x_0 = 1$.

Solution : La fonction fournie est $\displaystyle f(x)=x^2-2x+3$, et nous devons trouver l'approximation linéaire autour du point x = 1. Nous avons donc d'abord besoin de la dérivée.

$ \displaystyle \frac{d}{dx}\left(x^2-2x+3\right)$

By linearity: $\frac{d}{dx}\left( x^2-2x+3 \right) = \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(3\right)$, so plugging that in:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(3\right)$

The derivative of a constant is 0, so then:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)$

Directly: $\frac{d}{dx}\left( 2x \right) = 2$ and using the Power Rule for polynomial terms: $\frac{d}{dx}\left( x^2 \right) = 2x$

$ \displaystyle = \,\,$

$\displaystyle 2x-2$

Approximation Linéaire : L'équation de l'approximation linéaire que nous recherchons au point $x_0 = 2$ est donnée par la formule suivante

\[y = y_0 + f'(x_0)(x - x_0) \]

Remarquez que par définition $\displaystyle y_0 = f(x_0)$, ce qui implique que nous devons brancher la fonction au point $x_0 = 2$ :

\[y_0 = f(x_0) = f\left(2\right) = 2^2-2\cdot 2+3 = 3\]

Nous faisons la même chose, mais maintenant pour la dérivée au point $x_0 = 2$, alors

\[f'(x_0) = f'\left(2\right) = 2\cdot 2-2 = 2 \]

Avec ceci, nous revenons à la formule d'approximation linéaire :

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 3+2\left(x-2\right) = 2x-1 \]

Conclusion : Nous concluons que l'approximation linéaire de $\displaystyle f(x)=x^2-2x+3$ à $x_0 = 2$ est donnée par :

\[y = 2x-1 \]

Graphiquement :

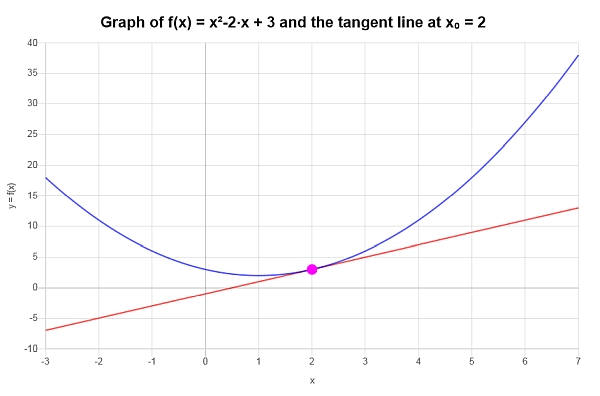
Exemple D'Approximation Du Premier Ordre

Exemple : plus d'approximation du premier ordre

Pour la fonction : $f(x) = x \sin(x)$ et le point $x_0 = 2$, trouver l'approximation du premier ordre correspondante.

Solution : Dans ce cas, la fonction que nous devons travailler est : $\displaystyle f(x)=x\sin\left(x\right)$.

Nous calculons maintenant sa dérivée :

$ \displaystyle \frac{d}{dx}\left(x\sin\left(x\right)\right)$

Using the Product Rule: $\frac{d}{dx}\left( x\sin\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)$

Directly differentiating: $\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \cos\left(x\right)$

Finally, simplifying

$ \displaystyle = \,\,$

$\displaystyle x\cos\left(x\right)+\sin\left(x\right)$

Approximation Linéaire : L'équation de l'approximation linéaire est :

\[y = y_0 + f'(x_0)(x - x_0) \]

où $\displaystyle y_0 = f(x_0)$, nous calculons alors :

\[y_0 = f(x_0) = f\left(2\right) = 2\sin\left(2\right)\]

Pour la dérivée à $x_0 = 2$ nous trouvons que :

\[f'(x_0) = f'\left(2\right) = 2\cos\left(2\right)+\sin\left(2\right) \]

Nous sommes maintenant prêts à les réintégrer dans la formule d'approximation du premier ordre :

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 2\sin\left(2\right)+2\cos\left(2\right)+\sin\left(2\right)\left(x-2\right) = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

Conclusion : On conclut que l'approximation linéaire de $\displaystyle f(x)=x\sin\left(x\right)$ au point donné $x_0 = 2$ est calculée comme suit :

\[y = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

Graphiquement, nous obtenons le graphique suivant :

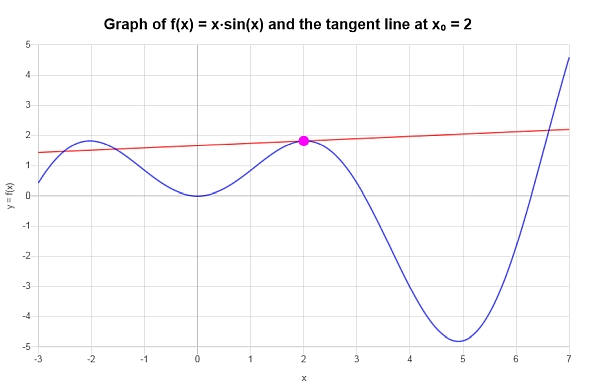
Exemple : calcul par approximation linéaire

Calculer l'approximation du premier ordre pour $ f(x) = \frac{\sin(x)}{x}$ à $x = \frac{\pi}{4}$.

Solution : La fonction suivante a été fournie : $\displaystyle f(x)=\frac{\sin\left(x\right)}{x}$, pour laquelle nous devons calculer sa dérivée.

La fonction est déjà simplifiée, nous pouvons donc procéder directement au calcul de sa dérivée :

$ \displaystyle \frac{d}{dx}\left(\frac{\sin\left(x\right)}{x}\right)$

Using the Quotient Rule: $\frac{d}{dx}\left( \frac{\sin\left(x\right)}{x} \right) = \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}$

$ \displaystyle = \,\,$

$\displaystyle \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}$

We know that $\frac{d}{dx}\left(x\right) = 1$

$ \displaystyle = \,\,$

$\displaystyle \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)}{x^2}$

Directly differentiating: $\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{x \cdot \cos\left(x\right)-\sin\left(x\right)}{x^2}$

Therefore, we get

$ \displaystyle = \,\,$

$\displaystyle \frac{x\cos\left(x\right)-\sin\left(x\right)}{x^2}$

Approximation Du Premier Ordre : L'équation de l'approximation du premier ordre correspondante pour la fonction donnée $\displaystyle f(x)=\frac{\sin\left(x\right)}{x}$ au point donné $x_0 = \frac{\pi}{4}$ est donnée par ce qui suit :

\[y = y_0 + f'(x_0)(x - x_0) \]

En branchant les valeurs correspondantes :

\[y_0 = f(x_0) = f\left(\frac{\pi}{4}\right) = \frac{\sin\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}} = \frac{2\sqrt{2}}{\pi{}}\] \[f'(x_0) = f'\left(\frac{\pi}{4}\right) = \frac{\cos\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}}-\frac{\sin\left(\frac{\pi{}}{4}\right)}{\left(\frac{\pi{}}{4}\right)^2} = \frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2} \]

Donc maintenant on peut mettre ça dans la formule :

\[y = y_0 + f'(x_0)(x - x_0) \] \[\Rightarrow y = \frac{2\sqrt{2}}{\pi{}}+\frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2}\left(x-\frac{1}{4}\pi{}\right) = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

Conclusion : Nous pouvons donc conclure que l'approximation du premier ordre pour la fonction donnée $\displaystyle f(x)=\frac{\sin\left(x\right)}{x}$ au point donné $x_0 = \frac{\pi}{4}$ est donnée par

\[y = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

Le résultat suivant est obtenu graphiquement :

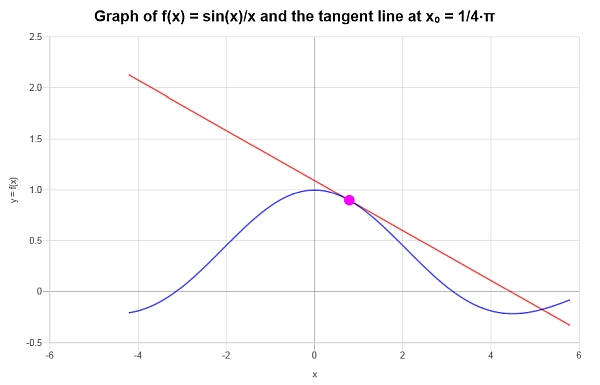
Plus de calculateurs de dérivés

Par ailleurs calculateur de linéarisation vous pouvez en trouver beaucoup qui font différentes choses basées sur les dérivées. La différenciation est une opération cruciale en calcul, en physique, en ingénierie et en économie, avec un large éventail d'applications.

Il existe également un moyen d'effectuer une approximation linéaire pour un plus grand nombre de variables, par exemple pour une fonction \f(x, y)\), auquel cas la formule d'approximation linéaire devient $f(x, y) = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0)(x-x_0) + \frac{\partial f}{\partial y}(x_0, y_0)(y-y_0)$, donc dans ce cas, afin de trouver la linéarisation, nous devons utiliser dérivés partiels .

Trouver la linéarisation d'une fonction n'est pas, et de loin, la seule chose que l'on peut faire avec les dérivées. La différentiation est une opération relativement facile avec des règles simples telles que le Règle Du Produit , la règle du quotient et le Règle De La Chaîne qui fait du calcul des dérivés une opération relativement simple.

Bien que cela soit censé être simple, il est bon d'utiliser une calculatrice de dérivées pour obtenir toutes les étapes indiquées, avec une mention claire de toutes les Règles relatives aux produits dérivés utilisé.