En savoir plus sur les inégalités quadratiques

Ce calcul d'inégalité quadratique vous fournira des solutions à des inégalités montrant toutes les étapes. Par exemple, l'inégalité que vous fournissez peut ressembler à 'x^2 - 1/2 > 0', et en général, les inégalités quadratiques ne sont pas trop difficiles à résoudre.

Une fois que vous avez fourni une inégalité valide impliquant expression quadratique vous pouvez cliquer sur "Calculer" pour obtenir toutes les étapes du calcul, y compris un graphique des solutions de l'inégalité.

inégalités quadratiques sont l'un des rares types (avec les inégalités linéaires ) que vous êtes assuré de trouver une solution exacte, et ce processus implique la résolution d'une équation quadratique.

Quelle est la définition de ce type d'inégalité ?

Nous ne l'avons pas énoncé explicitement, mais cela ressort assez clairement de son nom : une inégalité quadratique est un type spécifique d'inégalité dans laquelle tous les termes impliqués sont des polynômes de degré 2 au maximum. Dans ce contexte, un exemple est

\[\displaystyle x^2 < x - 1\]

qui est quadratique du fait que les deux côtés de l'inégalité sont des polynômes d'ordre au plus 2. Maintenant, si vous aviez :

\[\displaystyle x^2 < x^3 - 1\]

alors l'inégalité n'est plus quadratique, à cause du terme \(x^3\) du côté droit. Pour ces inégalités, nous disposons d'une feuille de route claire pour trouver la solution.

Étapes de la résolution d'inéquations quadratiques

• Étape 1 : Assurez-vous que vous avez une inégalité quadratique, car la méthode utilisée dans ce cas n'est valable que pour ce type d'inégalité
• Étape 2 : Comme pour la plupart des inégalités, il faut passer tout ce qui se trouve du côté gauche de l'inégalité et résoudre l'équation associée
• Étape 3 : Si l'équation quadratique associée n'a pas de racines réelles, nous savons alors que soit la droite réelle entière est une solution, soit il n'y a pas de solution. On teste donc n'importe quel point pour voir s'il résout l'inégalité, et si c'est le cas, la solution est la droite réelle entière (-∞, ∞), sinon, la solution est vide.
• Étape 4 : Si l'équation quadratique associée n'a qu'une seule solution réelle, cela signifie que le graphique quadratique associé touche tangentiellement l'axe des x. Ainsi, selon le signe de l'inégalité, la solution peut être uniquement le point de contact, ou tout sauf le point de contact, ou encore toute la ligne réelle (-∞, ∞), pour laquelle vous devez tester le point de contact et un point en dehors de celui-ci (à gauche et à droite du point)
• Étape 4 : Si l'équation quadratique associée a deux solutions réelles différentes, vous vérifiez les intervalles définis par ces racines pour déterminer quelles portions de la ligne réelle feront partie de la solution

Une fois que vous avez analysé les morceaux, si nécessaire, vous les joignez en utilisant l'opérateur "union", qui est utilisé pour assembler des intervalles.

Comment dessiner une inégalité quadratique ?

Représentation graphique des inégalités est un excellent moyen de comprendre visuellement à quoi ressemble la solution. En ce qui concerne la procédure, vous devez savoir si vous travaillez avec une inégalité à une variable ou si vous avez plusieurs variables.

Si vous avez une inégalité telle que

\[\displaystyle x^2 - \frac{1}{2} x < 1 \]

vous n'avez qu'une seule variable, et alors la solution sera un sous-ensemble de la ligne réelle. D'un autre côté, si vous aviez quelque chose comme

\[\displaystyle y < x^2 - \frac{1}{2} x \]

alors vous n'avez que deux variables x et y, et la solution de l'inégalité sera un sous-ensemble du plan x-y.

Importance des expressions quadratiques

Les expressions quadratiques impliquées dans les équations et les inégalités jouent un rôle fondamental en mathématiques. Après les expressions linéaires, les expressions quadratiques sont peut-être le type de structure le plus utilisé.

En calcul et en algèbre, vous trouverez d'innombrables applications des quadratiques dans les problèmes de maximisation et de minimisation, d'intégration et bien plus encore. En creusant un peu, vous trouverez des applications d'expressions quadratiques dans les différentes disciplines scientifiques

Exemple : inégalités quadratiques

Résolvez cette inégalité quadratique : \(\frac{1}{3}x^2 + \frac{5}{4}x - \frac{5}{6} < 0\)

Solution :

Nous devons d'abord résoudre l'équation auxiliaire quadratique suivante \(\displaystyle \frac{1}{3}x^2+\frac{5}{4}x-\frac{5}{6}=0\).

Application de la formule quadratique

L'équation quadratique est :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

Dans ce cas, nous avons :

\[a = \frac{1}{3}\] \[b = \frac{5}{4}\] \[c = -\frac{5}{6}\]

En introduisant ces valeurs dans la formule des racines, on obtient :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\left(\frac{5}{4}\right)^2-4\left(\frac{1}{3}\right)\left(-\frac{5}{6}\right)}}{2\cdot \frac{1}{3}} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\frac{385}{144}}}{\frac{2}{3}}\]

donc, nous trouvons que :

\[ {x}_1 = -\frac{\frac{5}{4}}{\frac{2}{3}}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{1}{8}\sqrt{385}-\frac{15}{8} \] \[{x}_2 = -\frac{\frac{5}{4}}{\frac{2}{3}}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{1}{8}\sqrt{385}-\frac{15}{8}\]

Points critiques

La liste des points critiques trouvés, classés par ordre croissant, est la suivante : \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}\), \(\frac{1}{8}\sqrt{385}-\frac{15}{8}\).

Ensuite, nous devons analyser les intervalles critiques suivants :

- Pour l'intervalle \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) : Le côté gauche est positif, donc \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) ne fait pas partie de la solution.

- Pour l'intervalle \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) : Le côté gauche est négatif, ce qui implique que \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) fait partie de la solution.

- Pour l'intervalle \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\) : Le côté gauche est positif, ce qui signifie que \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\) ne fait pas partie de la solution.

La solution

En se basant sur l'inégalité fournie et en analysant les points critiques, on trouve que la solution de l'inégalité est : \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}< x \le \frac{1}{8}\sqrt{385}-\frac{15}{8}\).

En utilisant la notation par intervalles, la solution s'écrit comme suit :

\[\left[-\frac{1}{8}\sqrt{385}-\frac{15}{8},\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\]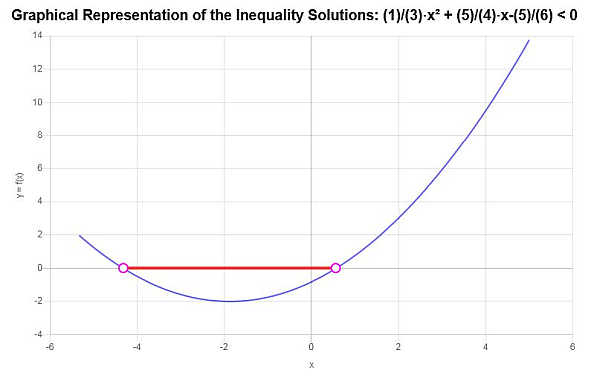

Exemple : autres inégalités quadratiques

Résoudre : \(x^2 < 4\)

Solution :

L'inégalité donnée est :

\[x^2 < 4\]

ce qui donne l'équation quadratique \(\displaystyle x^2-4=0\).

Formule quadratique

Pour une équation quadratique de la forme \(a x^2 + bx + c = 0\), les racines sont calculées comme suit formule quadratique :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

Dans ce cas, l'équation à résoudre est \(\displaystyle x^2-4 = 0\), ce qui implique que les coefficients correspondants sont :

\[a = 1\] \[b = 0\] \[c = -4\]

Tout d'abord, nous allons calculer le discriminant pour évaluer la nature des racines. Le discriminant est calculé comme suit :

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 16\]

Puisque dans ce cas le discriminant est \(\Delta = \displaystyle 16 > 0\), qui est positif, nous savons que l'équation a deux racines réelles différentes.

En introduisant ces valeurs dans la formule des racines, nous obtenons :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{16}}{2}\]

donc, nous trouvons que :

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{16}=\frac{0}{2}-2\cdot 1=\frac{0}{2}-2=-2 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{16}=\frac{0}{2}+2\cdot 1=\frac{0}{2}+2=2\]

Dans ce cas, l'équation quadratique \( \displaystyle x^2-4 = 0 \), a deux racines réelles, donc :

\[\displaystyle x^2-4 = \left(x+2\right)\left(x-2\right)\]

alors le polynôme original est factorisé en \(\displaystyle p(x) = x^2-4 = \left(x+2\right)\left(x-2\right) \), ce qui complète la factorisation.

Analyse des points critiques

La liste des points critiques trouvés, classés par ordre croissant, est la suivante : \(-2\), \(2\).

Sur cette base, nous devons analyser les intervalles suivants :

- Pour l'intervalle \(\left(-\infty, -2\right)\) : Le côté gauche est positif, donc \(\left(-\infty, -2\right)\) ne fait pas partie de la solution.

- Pour l'intervalle \(\left(-2, 2\right)\) : Le côté gauche est négatif, donc \(\left(-2, 2\right)\) fait partie de la solution.

- Pour l'intervalle \(\left(2, \infty\right)\) : Le côté gauche est positif, ce qui signifie que \(\left(2, \infty\right)\) ne fait pas partie de la solution.

Solution à l'inégalité

En se basant sur l'inégalité fournie et en analysant les points critiques, on trouve que la solution de l'inégalité est : \(-2< x \le 2\).

En utilisant la notation par intervalles, la solution s'écrit comme suit :

\[\left[-2,2\right)\]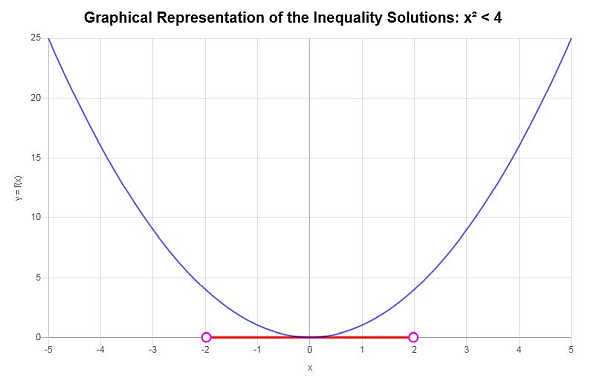

Autres calculateurs d'inégalité utiles

Le type d'inégalité le plus simple que vous pourrez résoudre est le suivant inégalités linéaires . Ensuite, vous avez des inégalités quadratiques, en termes de facilité.

Ensuite, vous avez inégalités polynomiales en général, d'un degré supérieur à 2. Ces questions devraient être simples, mais elles pourraient néanmoins constituer des tâches redoutables en termes de quantité de travail laborieux nécessaire pour les résoudre.

Disposer d'un calculatrice d'inégalité pour les inégalités en général peut s'avérer très utile, car il aborde les différents types d'inégalités qui se prêtent à la recherche de solutions exactes.