En savoir plus sur cette calculatrice d'inégalités linéaires

Cette calculatrice vous fournira les outils nécessaires pour traiter les inégalités linéaires. Plus précisément, vous serez en mesure de les résoudre et de les représenter graphiquement, en suivant toutes les étapes indiquées.

Les inégalités linéaires telles que "2x + 3 < 1" ou "3x + 2y <=1" sont autorisées et, en fonction du nombre de variables, vous obtiendrez un graphique approprié ainsi que les étapes menant à la solution.

Une fois qu'une inégalité linéaire valide a été fournie, il vous suffit de cliquer sur "Solve" pour lancer le processus. Si quelque chose n'est pas correct ou manque, la calculatrice vous le signalera.

Ce type d'inégalités est le plus simple que vous puissiez trouver et il est toujours relativement facile à résoudre. Ce type d'inéquation, ainsi que inégalités quadratiques sont parmi les seules inégalités "faciles" à résoudre.

Qu'est-ce qu'une inégalité linéaire ?

Une inégalité linéaire est le type d'inégalité le plus simple, dans lequel tous les termes impliqués sont linéaires ou constants.

\[\displaystyle a x + b y \le 1\]

Par exemple, l'équation ci-dessus est une équation linéaire à deux variables. Techniquement parlant, nous avons inégalité polynomiale de degré 1, mais c'est une façon un peu trop compliquée de voir les choses.

Comment résoudre une inégalité linéaire ?

• Étape 1 : Mettez d'un côté tout ce qui contient la variable que vous voulez résoudre et de l'autre le reste
• Étape 2 : Groupe et simplifier l'expression , de sorte que pour réduire les termes analogues
• Étape 3 : Si une constante différente de un multiplie la variable que vous voulez résoudre, divisez-la. Une mise en garde s'impose : si vous divisez par une valeur négative, vous devez changer le sens de l'inégalité

L'un des principaux points à garder à l'esprit, et qui différencie les processus de résolution d'équations et d'inéquations, est que lors de la résolution d'équations, nous pouvons plus librement multiplier (ou diviser) par des constantes sans que rien ne change, alors qu'avec les inéquations, nous devons être plus prudents, car multiplier (ou diviser) par des constantes négatives modifie le sens de l'inégalité.

Quelle est l'inégalité linéaire la plus générale ?

Le plus général que l'on puisse obtenir avec un système linéaire est

\[\displaystyle a x + bx \le c\]

mais il se peut que vous ayez "<" au lieu de "\(\le\)". Ou nous pourrions avoir

\[\displaystyle a x + bx \ge c\]

mais vous pouvez aussi utiliser '>' au lieu de '\(\ge\)'.

Comme pour l'addition et la soustraction, la division de fractions est simplement dérivée de la multiplication de fractions : Pour diviser deux fractions, il suffit de multiplier la première par la seconde fraction inverse du second (la fraction inverse est obtenue en échangeant le numérateur par le dénominateur dans la fraction).

Applications

Les inégalités linéaires trouvent de nombreuses applications en mathématiques. Une inégalité linéaire est un type de moyenne pondérée, qui convient parfaitement à toutes sortes de problèmes de mélange et d'affectation.

Lorsque l'on traite des problèmes de mots, on trouve généralement des équations linéaires, mais il n'est pas rare que l'on ait également affaire à des inéquations linéaires.

L'un des domaines les plus connus est celui de l'optimisation et de la programmation linéaire, dans lequel les inégalités linéaires jouent un rôle crucial, à la fois avec la méthode du simplexe et avec les conditions de Kuhn-Tucker lorsqu'il s'agit d'une fonction objective non linéaire.

Exemple : résoudre des inégalités

Résolvez l'inégalité linéaire suivante : \(\frac{2}{3} x + \frac{5}{4} < - \frac{1}{6}\)

Solution :

Nous devons mettre de côté tous les termes de l'inégalité :

\[\frac{2}{3}x+\frac{5}{4}- \left(-\frac{1}{6}\right)< 0\]

Équation auxiliaire associée

Nous devons trouver une solution :

\[\frac{2}{3}x+\frac{5}{4}-\left(-\frac{1}{6}\right)=0\]

Étape 0 : Dans ce cas, nous devons d'abord simplifier l'équation linéaire donnée, et pour ce faire, nous procédons aux étapes de simplification suivantes :

Résolution de l'équation linéaire

En plaçant \(x\) du côté gauche et la constante du côté droit, nous obtenons

\[\displaystyle \frac{2}{3}x = -\frac{17}{12}\]

Maintenant, en résolvant \(x\), en divisant les deux côtés de l'équation par \(\frac{2}{3}\), on obtient ce qui suit

\[\displaystyle x = \displaystyle \frac{ -\frac{17}{12}}{ \frac{2}{3}}\]

et en simplifiant on obtient finalement ce qui suit

\[\displaystyle x=-\frac{17}{8}\]

Par conséquent, la résolution de \(x\) pour une équation linéaire donnée conduit à \(x=-\frac{17}{8}\).

Points critiques

Comme prévu pour une inégalité linéaire, il n'y a qu'un seul point critique, qui est \(-\frac{17}{8}\), à partir duquel nous analysons les intervalles suivants :

- Pour l'intervalle \(\left(-\infty, -\frac{17}{8}\right)\) : Le côté gauche est négatif, ce qui signifie que \(\left(-\infty, -\frac{17}{8}\right)\) fait partie de la solution.

- Pour l'intervalle \(\left(-\frac{17}{8}, \infty\right)\) : Le côté gauche est positif, ce qui implique que \(\left(-\frac{17}{8}, \infty\right)\) ne fait pas partie de la solution.

Solution à l'inégalité

On constate donc que la solution de l'inégalité est : \(x < -\frac{17}{8}\).

L'expression de la solution avec la notation d'intervalle, la solution s'écrit comme suit :

\[\left(-\infty,-\frac{17}{8}\right)\]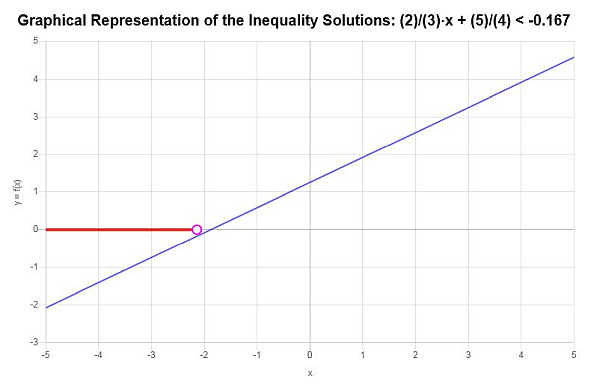

Exemple : autres inégalités linéaires

Résolvez cette inégalité linéaire à 2 variables : \(\frac{1}{3} x + \frac{5}{4} y < - \frac{5}{6}\)

Solution :

Nous devons trouver une solution :

\[\frac{1}{3}x+\frac{5}{4}y < -\frac{5}{6}\]

Nous avons une inégalité linéaire donnée, et nous devons résoudre la variable \(y\).

Dans ce cas, nous résolvons \(y\), donc en le plaçant d'un côté de l'inégalité et le reste de l'autre côté, nous obtenons :

\[\frac{5}{4}y<-\frac{1}{3}x-\frac{5}{6}\]

Afin de résoudre \(y\), nous divisons les deux côtés de l'inégalité par \(\frac{5}{4}\) pour obtenir finalement :

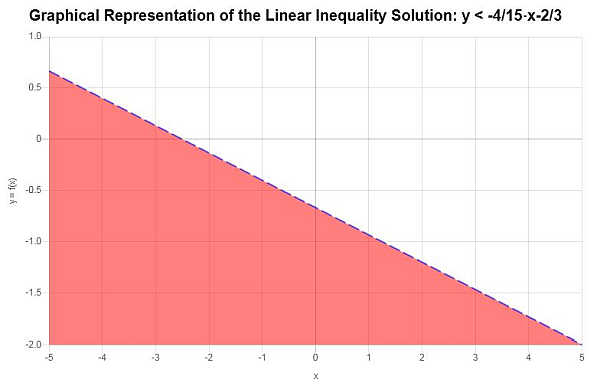
\[y < -\frac{4}{15}x-\frac{2}{3}\]

Solution d'une inégalité linéaire

Sur la base de l'inégalité fournie, après l'avoir résolue pour \(y\), nous obtenons :

\[y < -\frac{4}{15}x-\frac{2}{3}\]

La représentation graphique de la région de solution est illustrée dans le graphique ci-dessous :

Plus de calculatrices d'algèbre

Le traitement de l'expression est crucial en algèbre. Simplification de l'expression est le point de départ de la plupart des processus mathématiques, et il est généralement nécessaire de réduire les choses à leur expression la plus simple.

Résolution d'équations et aussi Résolution d'inéquations restera au cœur de la plupart des processus, car l'un ou l'autre sera au centre de presque tout ce que vous ferez en mathématiques.