Calculatrice d'inégalité
Instructions : Utilisez la calculatrice d'inégalité pour résoudre n'importe quelle inégalité que vous fournissez, en montrant toutes les étapes. Veuillez saisir l'inégalité que vous souhaitez résoudre dans la case ci-dessous :
En savoir plus sur la résolution d'inégalités
Cette calculatrice vous permet de résoudre les inégalités que vous fournissez. Tout ce que vous avez à faire est de taper l'inégalité souhaitée dans la case, et de vous assurer que vous fournissez une inégalité valide.
Par exemple, vous pouvez fournir quelque chose comme "2x^2 - x >= 1/2", ou quelque chose comme "sin(x) > 0", tant que vous fournissez des éléments valides. Veillez également à utiliser un signe d'inégalité, tel que ">", "<", ">=" ou "<=".
Si, à la place, vous utilisez "=", cette calculatrice agira en tant que calculatrice d'équations .
Une fois que vous avez fourni une inégalité valide, l'étape suivante consiste à cliquer sur "Résoudre" et, en une fraction de seconde, vous obtiendrez la solution étape par étape. Une mise en garde s'impose : toutes les inégalités ne pourront pas être résolues, gardez-le à l'esprit.
Toutes les inégalités ne sont pas faciles à résoudre, et nous ne pouvons pas non plus appliquer certaines méthodes préconçues. Seuls certains types, tels que inégalités linéaires , inégalités quadratiques ou égalités polynomiales (pour les degrés inférieurs) admettre un traitement systématique.

Qu'est-ce qu'une inégalité ?
Une inégalité est un type d'objet mathématique qui ressemble beaucoup à une équation mathématique à la différence qu'au lieu de "=", une inégalité contient soit ">", "<", ">=" ou "<=". Cette petite différence d'apparence rend la résolution d'une inégalité plus complexe que celle d'une équation.
Par exemple, l'expression ci-dessous est une inégalité
\[\displaystyle x + \frac{1}{3} < x^2 \]Il s'agit donc d'une expression mathématique qui a deux côtés, le côté gauche et le côté droit, et dont le signe d'inégalité correspondant est "<". On dit que l'inégalité ci-dessus est une inégalité quadratique, car les expressions des côtés gauche et droit sont toutes deux polynomiales, et le degré le plus élevé est 2.
Par exemple, l'inégalité ci-dessous est une inégalité trigonométrique :
\[\displaystyle x + \frac{1}{3} \le \sin\left(x^2 + \frac{1}{x}\right) \]Il s'agit d'une inégalité car elle comporte le signe d'inégalité \(\le\), et le côté droit contient un expression trigonométrique . Observez que la première inégalité est assez simple à résoudre, alors que l'autre est loin d'être facile, et vous ne pouvez même pas la résoudre.
Comment résoudre une inégalité
En règle générale, nous trouverons la solution des inégalités en résolvant d'abord une équation associée. La résolution de l'inégalité sera plus difficile si l'équation associée est plus difficile à résoudre. Les étapes suivantes vous aideront dans le processus de résolution :
- Étape 0 : Simplifier les expressions impliqués dans l'inégalité. Il est presque toujours plus facile de résoudre une inégalité simplifiée que l'inégalité originale
- Étape 1 : Identifiez l'inégalité que vous voulez résoudre, et identifiez soigneusement le signe de l'inégalité (>, ≥, <, ≤). Si vous avez "=", vous devez alors utiliser un calculatrice d'équations au lieu de
- Étape 2 : Vous écrivez ensuite l'équation associée, qui est simplement obtenue en remplaçant le signe d'inégalité trouvé à l'étape précédente, puis en le remplaçant par le signe d'égalité "="
- Étape 3 : Résoudre l'équation associée. Vous déterminerez la solution de l'inégalité en vous basant sur l'existence de solutions réelles à votre équation associée, et en prenant des notes sur tous les points qui peuvent rendre l'expression indéfinie
- Étape 4 : Si votre équation associée n'a pas de solution réelle : Dans ce cas, vous savez que l'équation n'est jamais nulle, au moins pour les valeurs réelles. Dans ce cas, et en supposant la continuité, soit tous les points sont une solution de l'inégalité, soit aucun ne l'est. Vous évaluez donc l'inégalité en tout point (disons x = 0), et si elle tient, alors toutes les valeurs réelles sont solutions de l'inégalité, et si elle ne tient pas, alors il n'y a pas de solutions réelles
- Étape 5 : Enfin, supposons qu'il existe des solutions réelles à l'équation associée. Nous appellerons ces solutions des points critiques, et nous ajouterons à la liste des points critiques tous les points où l'expression devient indéfinie (divisions par zéro, etc.)
- Étape 6 : S'il n'y a qu'un seul point critique, que nous appelons "a" : évaluez l'inégalité en tout point à gauche de "a", et si elle tient, l'intervalle (-∞, a) fera partie de l'ensemble de solutions. Si l'inégalité est "<=" or ">=", vous incluez le point final, enfin (-∞, a). On procède de la même manière pour un point situé à droite de "a", et si l'inégalité est valable pour ce point, alors (-∞, a) fera partie de l'ensemble de solutions
- Étape 7 : Un processus similaire est mis en œuvre s'il existe plus d'un point critique : Prenez deux points critiques consécutifs, que nous appelons "a1" et "a2" : Évaluez l'inégalité en tout point situé entre a1 et a2, et si elle est valable, l'intervalle (a1, a2) fera partie de l'ensemble de solutions. Si l'inégalité est "<=" or ">= ", alors vous incluez les points d'extrémité
Cela semble compliqué, mais il suffit d'être systématique. Par exemple, si votre inégalité est \(\displaystyle x + \frac{1}{3} < x^2 \), alors l'équation associée est \(\displaystyle x + \frac{1}{3} = x^2 \), qui est facile à résoudre, puisqu'il s'agit d'un Equation quadratique .
Ensuite, dans le cadre de l'analyse des points critiques (s'il y en a), représentation graphique de la solution de l'inégalité peut rendre les choses plus claires. Dans certains cours d'algèbre, les étudiants apprennent à utiliser une tabulation pour garder une trace de ce qui se passe entre les points critiques, ce qui pourrait être très utile.
Quelle est la différence avec un système d'inégalités ?
Un système d'inégalités est constitué de plusieurs inégalités simultanées qui doivent être résolues en même temps. Cela semble plus difficile que de résoudre une simple inégalité parce que c'est plus difficile. Si la résolution d'inégalités peut s'avérer laborieuse, c'est encore plus vrai pour les systèmes d'inéquations.
Un exemple de système d'inégalités est présenté ci-dessous :
\[\displaystyle x + y < 1 \] \[\displaystyle 2x + y^2 \le 1 \]Dans l'exemple ci-dessus, vous avez un système d'inégalités à résoudre. Ce système d'inéquations comporte deux inéquations et deux inconnues (x et y).
Comme vous pouvez probablement l'imaginer, la résolution d'un système d'inéquations peut être difficile en général. Nous nous concentrerons principalement sur la résolution de systèmes d'équations linéaires, qui sont étroitement liés aux systèmes d'inéquations la résolution d'un système d'équations linéaires

Avantages de l'utilisation de cette calculatrice d'inégalité avec étapes
En réalité, il sera difficile de résoudre la plupart des inégalités. Seules quelques-unes d'entre elles, avec des structures très spécifiques, se prêteront à l'analyse. La majorité d'entre elles ne le seront pas, il vaut donc mieux s'y préparer.
- Avantage 1 : Gagner beaucoup de temps : La résolution d'inéquations peut prendre beaucoup de temps, car il faut d'abord résoudre l'équation associée, puis analyser les points critiques
- Avantage 2 : Veillez à mettre toutes les chances de votre côté pour la résoudre : Comme vous le savez probablement déjà, toutes les équations ou inéquations ne peuvent pas être résolues facilement, voire pas du tout. Une calculatrice avec étapes tentera la meilleure approche possible en fonction de la structure détectée
- Avantage 3 : Obtenez des résultats, étape par étape, d'une manière claire. Certaines calculatrices vous donnent la réponse finale mais n'affichent pas les étapes. Un graphique illustrant les solutions est également très utile
Pendant que vous apprenez les ficelles du métier, le fait d'avoir une calculatrice d'inégalités qui fait le gros du travail pour vous vous montrera la façon dont les choses sont faites, et vous acquerrez probablement les compétences nécessaires pour détecter les structures qui sont plus faciles à aborder.
Les inégalités ont-elles une utilité pratique ?
Et comment ! En mathématiques de base (algèbre et calcul 101), l'accent est mis sur les égalités et les équations. Le monde réel est plein de processus où nous n'avons pas nécessairement d'équations, mais où nous avons des inégalités qui proviennent de limites inférieures ou supérieures imposées par certaines contraintes physiques.
Certains domaines mathématiques avancés, comme les équations différentielles, fondent leurs cadres théoriques sur des inégalités (que les experts aiment appeler "estimations d'énergie" dans certains contextes).
L'importance des inégalités ne vous paraît peut-être pas évidente, ni la nécessité de les apprendre trop urgente, mais en réalité, les inégalités constituent l'une des pierres angulaires de la méthodologie mathématique utilisée pour construire des théories, bien que dans les jolis résultats finaux, nous ayons tendance à voir des égalités à la place.

Exemple : résoudre des inégalités
Calculer la solution de : \(\frac{1}{3}x + \frac{5}{4} \ge \frac{1}{6}\)
Solution : Nous devons placer tous les termes de l'inégalité dans le côté gauche (il pourrait s'agir du côté droit, mais il est plutôt conventionnel d'utiliser le côté gauche) :
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6}\ge 0 \]À partir de l'inégalité ci-dessus, nous obtenons l'équation linéaire associée qui doit être résolue en premier lieu :
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6} = 0 \]Étape 0 : Dans ce cas, nous devons d'abord simplifier l'équation linéaire donnée, et pour ce faire, nous procédons aux étapes de simplification suivantes :
Résolution de l'équation linéaire
En plaçant \(x\) du côté gauche et la constante du côté droit, nous obtenons
\[\displaystyle \frac{1}{3}x = -\frac{13}{12}\]Maintenant, en résolvant \(x\), en divisant les deux côtés de l'équation par \(\frac{1}{3}\), on obtient ce qui suit
\[\displaystyle x = \displaystyle \frac{ -\frac{13}{12}}{ \frac{1}{3}}\]et en simplifiant on obtient finalement ce qui suit
\[\displaystyle x=-\frac{13}{4}\]Par conséquent, la résolution de \(x\) pour une équation linéaire donnée conduit à \(x=-\frac{13}{4}\).
Analyse des points critiques
Le seul point critique trouvé est \(-\frac{13}{4}\).
Sur cette base, nous devons analyser les intervalles suivants :
- Pour l'intervalle \(\left(-\infty, -\frac{13}{4}\right)\) : Le côté gauche est négatif, donc \(\left(-\infty, -\frac{13}{4}\right)\) ne fait pas partie de la solution.
- Pour l'intervalle \(\left(-\frac{13}{4}, \infty\right)\) : Le côté gauche est positif, ce qui signifie que \(\left(-\frac{13}{4}, \infty\right)\) fait partie de la solution.
Solution à l'inégalité
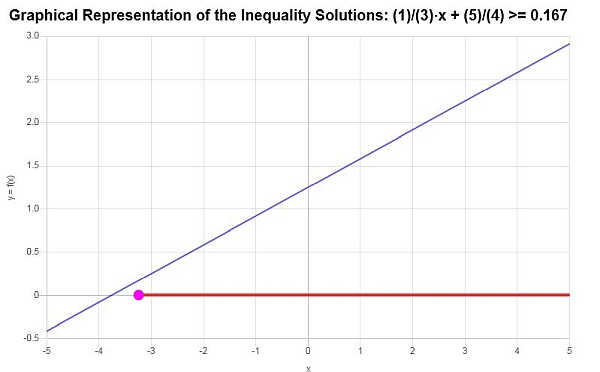
En se basant sur l'inégalité fournie et en analysant les points critiques, on trouve que la solution de l'inégalité est : \(x \ge -\frac{13}{4}\).
En utilisant la notation par intervalles, la solution s'écrit comme suit :
\[\left[-\frac{13}{4},\infty\right)\]La graphique d'inégalité linéaire de la solution obtenue est indiquée ci-dessous
Exemple : autres exemples d'inégalité
Trouvez la solution de ce qui suit : \(\sin(x) > 0\)
Solution : On nous donne l'inégalité trigonométrique suivante à résoudre :
\[\sin\left(x\right) > 0\]Traitement d'une équation auxiliaire
A partir de l'inégalité de trigonométrie ci-dessus, nous obtenons l'équation associée que nous devons résoudre en premier lieu :
\[\sin\left(x\right)=0\]Résolution de l'équation trigonométrique auxiliaire
alors les solutions sont : \(x = \pi{}K\), pour une constante entière arbitraire \(K\).
Analyse des points critiques
Sur la base des solutions de l'équation auxiliaire, la liste des points critiques trouvés est : \(\pi{}K\), pour une constante entière arbitraire \(K\).
Remarquez que nous disposons d'un nombre infini d'intervalles critiques, nous en analysons donc quelques-uns ci-dessous :
- Pour l'intervalle \(\left(-3\pi{}, -2\pi{}\right)\) : Le côté gauche est négatif, donc \(\left(-3\pi{}, -2\pi{}\right)\) ne fait pas partie de la solution.
- Pour l'intervalle \(\left(-2\pi{}, -\pi{}\right)\) : Le côté gauche est positif, ce qui signifie que \(\left(-2\pi{}, -\pi{}\right)\) fait partie de la solution.
- Pour l'intervalle \(\left(-\pi{}, 0\right)\) : Le côté gauche est négatif, ce qui signifie que \(\left(-\pi{}, 0\right)\) ne fait pas partie de la solution.
- Pour l'intervalle \(\left(0, \pi{}\right)\) : Le côté gauche est positif, ce qui signifie que \(\left(0, \pi{}\right)\) fait partie de la solution.
- Pour l'intervalle \(\left(\pi{}, 2\pi{}\right)\) : Le côté gauche est négatif, donc \(\left(\pi{}, 2\pi{}\right)\) ne fait pas partie de la solution.
- Pour l'intervalle \(\left(2\pi{}, 3\pi{}\right)\) : Le côté gauche est positif, ce qui signifie que \(\left(2\pi{}, 3\pi{}\right)\) fait partie de la solution.
C'est ainsi que nous procédons pour l'ensemble de la séquence d'intervalles.
Intervalles de solution partielle
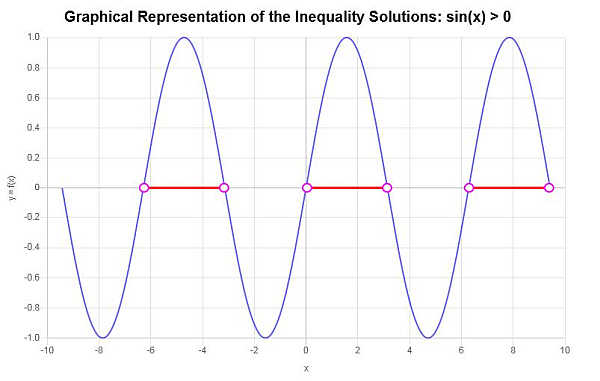
Sur la base de l'analyse des points critiques trouvés et des intervalles correspondants générés par les points critiques consécutifs, nous sommes en mesure d'identifier les éléments suivants comme faisant partie de la solution de l'inégalité :
\[\left(-2\pi{}, -\pi{}\right) \cup \left(0, \pi{}\right) \cup \left(2\pi{}, 3\pi{}\right)\]Dans ce cas, nous pouvons approximativement identifier différentes zones de solution, comme le montre le graphique ci-dessous. Les graphique d'inégalité donne la représentation graphique suivante de la solution trouvée :
Exemple : plus d'inégalités
Résoudre l'inégalité quadratique \( x^2 - 2x > 6 \).
Solution : L'inégalité que nous devons résoudre est la suivante
\[x^2-2x > 6\]En mettant tous les termes de l'inégalité d'un côté, nous obtenons :
\[x^2-2x-6>0\]Équation auxiliaire
Nous obtenons l'équation auxiliaire suivante, qui doit d'abord être résolue :
\[x^2-2x-6=0\]Nous avons une expression polynomiale sur le côté gauche, qui est \(\displaystyle deg(p) = 2\), son coefficient principal est \(\displaystyle a_{2} = 1\) et son coefficient constant est \(\displaystyle a_0 = -6\).
Formule quadratique
Dans ce cas, les racines sont calculées à l'aide de la formule suivante :
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\] \[\Rightarrow = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-6\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{28}}{2}\]donc, nous trouvons que :
\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{28}=\frac{2}{2}-\sqrt{7}=1-\sqrt{7}=-\sqrt{7}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{28}=\frac{2}{2}+\sqrt{7}=1+\sqrt{7}=\sqrt{7}+1\]Dans ce cas, l'équation quadratique \( \displaystyle x^2-2x-6 = 0 \), a deux racines réelles, qui deviennent des points critiques :
Analyse des points critiques
La liste des points critiques trouvés, classés par ordre croissant, est la suivante : \(-\sqrt{7}+1\), \(\sqrt{7}+1\).
Sur cette base, nous devons analyser les intervalles suivants :
- Pour l'intervalle \(\left(-\infty, -\sqrt{7}+1\right)\) : Le côté gauche est positif, ce qui implique que \(\left(-\infty, -\sqrt{7}+1\right)\) fait partie de la solution.
- Pour l'intervalle \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\) : Le côté gauche est négatif, donc \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\) ne fait pas partie de la solution.
- Pour l'intervalle \(\left(\sqrt{7}+1, \infty\right)\) : Le côté gauche est positif, ce qui signifie que \(\left(\sqrt{7}+1, \infty\right)\) fait partie de la solution.
Trouver la solution de l'inégalité
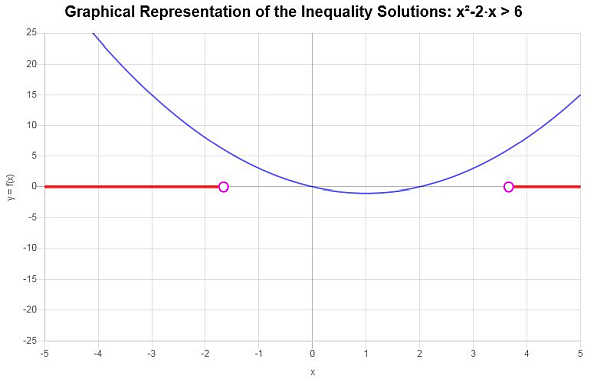
En se basant sur l'inégalité fournie et en analysant les points critiques, on trouve que la solution de l'inégalité est : \(x < -\sqrt{7}+1\) ou \(x > \sqrt{7}+1\).
En utilisant la notation par intervalles, la solution s'écrit comme suit :
\[\left(-\infty,-\sqrt{7}+1\right) \cup \left(\sqrt{7}+1,\infty\right)\]La solution de l'inégalité est représentée graphiquement :
Plus d'inégalités ci-dessus
Vous commencerez toujours par un calculatrice d'inégalités linéaires ou peut-être un calculatrice d'inégalités quadratiques car ce sont eux qui sont assurés de trouver une solution.
Ensuite, même avec un inégalité polynomiale vous pourriez vous heurter à des sables rapides, car les inégalités polynomiales peuvent également être délicates, voire impossibles à résoudre exactement avec des méthodes élémentaires.
Tout autre type d'inégalité dépendra de sa structure et d'une substitution astucieuse que vous pourriez trouver.




