Solveurs Calculus

Dérivés trigonométriques

Instructions: Utilisez la calculatrice de dérivée trigonométrique pour calculer la dérivée de toute fonction que vous fournissez qui implique des fonctions trigonométriques, en montrant toutes les étapes. Veuillez saisir la fonction que vous souhaitez différencier dans le champ de formulaire ci-dessous.

En savoir plus sur les dérivés trigonométriques

Utilisez cette calculatrice pour trouver des dérivées trigonométriques, que nous supposons dans ce cas être n'importe quelle fonction différentiable valide qui implique une ou plusieurs fonctions trigonométriques élémentaires.

Un exemple de fonction valide pour cette calculatrice est f(x) = sin(x)/x, ou f(x) = x*sin(x^3), juste pour donner un exemple.

Ensuite, lorsque vous avez déjà tapé la fonction correspondante, vous pouvez ensuite cliquer sur le bouton "Calculer", ainsi pour obtenir toutes les étapes du calcul de la dérivée qui vous sont présentées.

Les fonctions trigonométriques jouent un rôle crucial dans le calcul, ainsi que dans calcul des dérivées en général. En fin de compte, les fonctions plus complexes peuvent voir leurs dérivées réduites au calcul de la dérivée pour des fonctions trigonométriques plus simples.

Dérivés trigonométriques de base

L'idée d'utiliser des règles dérivées est de décomposer une fonction complexe et de la différencier en utilisant les dérivées de fonctions connues. Plus précisément, des fonctions trigonométriques simples comme le sinus, le cosinus, la tangente et la cotangente joueront un rôle important à cet égard.

Quelles sont les dérivées trigonométriques de base ?

Trig Dérivée 1 : $\frac{d}{dx} \sin (x) = \cos(x)$
Trig Dérivée 2 : $\frac{d}{dx} \cos (x) = -\sin(x)$
Trig Dérivée 3 : $\frac{d}{dx} \tan (x) = \sec^2(x)$
Trig Dérivée 4 : $\frac{d}{dx} \cot (x) = -\csc^2(x)$
Dérivée Trigonométrique 5 : $\frac{d}{dx} \sec (x) = \sec(x)\tan(x)$
Dérivée Trigonométrique 6 : $\frac{d}{dx} \sec (x) = -\csc(x)\cot(x)$

Ce sont les dérivés de base que vous devez connaître très, et éventuellement mémoriser afin d'utiliser Règles relatives aux produits dérivés pour calculer des dérivées plus compliquées

Les dérivées trigonométriques sont-elles en degrés ?

Non, les dérivées des fonctions trigonométriques sont dans radians , de sorte que les dérivées trigonométriques trouvées reflètent le fait que l'argument x est mesuré en radians.

Ainsi, par exemple, supposons que nous voulions calculer la dérivée de sin dans degrés , nous définissons donc $f(y) = \sin(y)$, où $y$ est mesuré en degrés.

Maintenant, laissez $x = \frac{\pi y}{180}$ être l'angle équivalent en radians et en résolvant également pour $y$ nous trouvons que $y = \frac{180 x}{\pi}$, donc en utilisant la règle de chaîne :

\[\displaystyle \frac{d}{dy} f(y) = \displaystyle \frac{d}{dy} f(y(x)) \frac{dy}{dx} = \frac{180}{\pi} \cos(y) \]

Donc, sur cette base, la dérivée du sinus en degrés est en fait un cosinus en degrés, mais multiplié par un facteur $\frac{180}{\pi}$.

Comment trouve-t-on les dérivées en trigonométrie ?

Les dérivés trigonométriques sont trouvés par définition, en utilisant des identités trigonométriques de base. Par exemple, en utilisant le formule du sinus de la somme on peut dériver la dérivée de $\sin(x)$, en utilisant la définition de limite :

\[\displaystyle \frac{d}{dx} \sin(x) = \displaystyle \lim_{h \to 0} \frac{\sin(x+h)-\sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)\cos(h) + \cos(x)\sin(h) - \sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)(\cos(h)-1) + \cos(x)\sin(h)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} + \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} \right)+ \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \displaystyle \lim_{h \to 0} \left( \frac{(\cos(h)-1)}{h} \right)+ \cos(x) \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \cdot 0 + \cos(x) \cdot 1 = \cos(x)\]

Conseils et astuces

Le principal point à retenir pour vous est de toujours vous rappeler ce que 6 dérivés trigonométriques sont , et les connaître par cœur, car vous les utiliserez en permanence, ainsi que les bases règles de différenciation .

De même, vous pouvez utiliser les identités trigonométriques et la définition de la fonction inverse pour trouver les dérivés trigonométriques inverses les plus courants.

Calculatrice De Dérivées Trigonométriques

Exemple : calcul de la dérivée trig

Considérez la fonction suivante : $f(x) = \sin^2(x)+ \frac{1}{x}$. Trouver sa dérivée

Solution: Les dérivés trigonométriques impliquent une fonction trigonométrique qui doit être différenciée. Considérez la fonction $\displaystyle f(x)=\sin\left(x\right)^2+\frac{1}{x}$, qui contient une fonction sinusoïdale, elle est donc qualifiée de dérivée trigonométrique.

$ \displaystyle \frac{d}{dx}\left(\sin\left(x\right)^2+\frac{1}{x}\right)$

By using the linearity property, we know $\frac{d}{dx}\left( \sin(x)^2+\frac{1}{x} \right) = \frac{d}{dx}\left(\sin(x)^2\right)+\frac{d}{dx}\left(\frac{1}{x}\right)$, so plugging that in:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(\sin\left(x\right)^2\right)+\frac{d}{dx}\left(\frac{1}{x}\right)$

Using the Power Rule for a polynomial term with negative exponent: $\frac{d}{dx}\left( \frac{1}{x} \right) = -\frac{1}{x^2}$ and in this case we can use the Power Rule for a constant exponent: $\frac{d}{dx}\left( \sin\left(x\right)^2 \right) = 2\sin\left(x\right)\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)$

$ \displaystyle = \,\,$

$\displaystyle 2\sin\left(x\right)\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\frac{1}{x^2}$

Directly differentiating: $\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)$

$ \displaystyle = \,\,$

$\displaystyle 2\sin\left(x\right)\cdot \cos\left(x\right)-\frac{1}{x^2}$

which then leads to

$ \displaystyle = \,\,$

$\displaystyle 2\sin\left(x\right)\cos\left(x\right)+\frac{-1}{x^2}$

Directly expanding and simplifying

$ \displaystyle = \,\,$

$\displaystyle \frac{2x^2\cos\left(x\right)\sin\left(x\right)-1}{x^2}$

Résultats : Pour cet exemple, on trouve que la dérivée est :

\[f'(x) = \frac{2x^2\cos\left(x\right)\sin\left(x\right)-1}{x^2}\]

Il est très utile de représenter la fonction et sa dérivée sur un graphique. Voir ci-dessous:

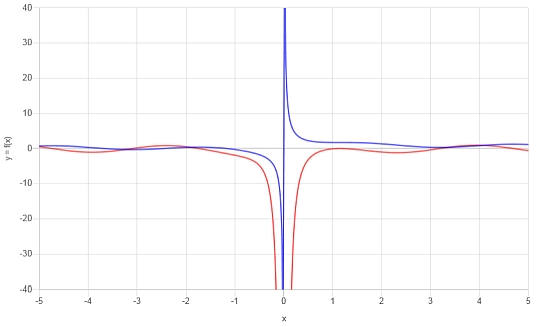
Exemple de dérivée d'une fonction trigonométrique

Considérez la fonction trigonométrique suivante : $f(x) = \sin(x) + x \cos(x)$, trouvez sa dérivée.

Solution: Maintenant, nous devons travailler avec la dérivée de la fonction trigonométrique suivante $\displaystyle f(x)=\sin\left(x\right)+x\cos\left(x\right)$.

$ \displaystyle \frac{d}{dx}\left(x\cos\left(x\right)+\sin\left(x\right)\right)$

By linearity, we know $\frac{d}{dx}\left( x\cos(x)+\sin(x) \right) = \frac{d}{dx}\left(x\cos(x)\right)+\frac{d}{dx}\left(\sin(x)\right)$, so plugging that in:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\cos\left(x\right)\right)+\frac{d}{dx}\left(\sin\left(x\right)\right)$

Directly differentiating: $\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)$ and we can use the Product Rule: $\frac{d}{dx}\left( x\cos\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x\right)+x \cdot \frac{d}{dx}\left(\cos\left(x\right)\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x\right)+x \cdot \frac{d}{dx}\left(\cos\left(x\right)\right)+\cos\left(x\right)$

By applying direct differentiation: $\frac{d}{dx}\left( \cos\left(x\right) \right) = -\sin\left(x\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x\right)+x \left(-\sin\left(x\right)\right)+\cos\left(x\right)$

and then we find

$ \displaystyle = \,\,$

$\displaystyle x\cdot \left(-\sin\left(x\right)\right)+\cos\left(x\right)+\cos\left(x\right)$

We group together the terms that are multiplying $\cos\left(x\right)$ and then simplifying $1+1 = 2$

$ \displaystyle = \,\,$

$\displaystyle x\cdot \left(-\sin\left(x\right)\right)+2\cos\left(x\right)$

By reorganizing the terms:

$ \displaystyle = \,\,$

$\displaystyle -x\sin\left(x\right)+2\cos\left(x\right)$

Conclusion Finale : Nous concluons que la dérivée est donnée par :

\[f'(x) = -x\sin\left(x\right)+2\cos\left(x\right)\]

Le tracé suivant est obtenu :

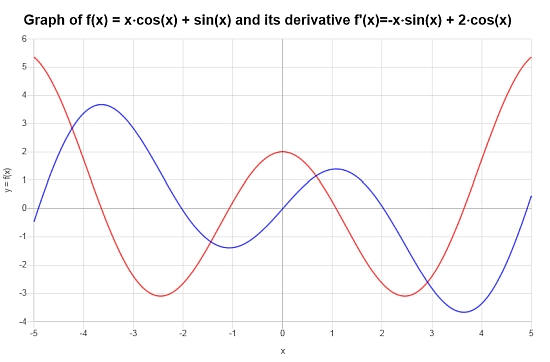
Exemple : dérivées trigonométriques et différenciation implicite

Trouvez $\frac{dy}{dx}$ pour $ \sin(x)+\cos(y) = 1 $.

Solution: Nous devons utiliser différenciation implicite , nous différencions donc les deux côtés et utilisons le Règle De La Chaîne :

\[ \frac{dy}{dx}\left(\sin(x)+\cos(y)\right) = \frac{dy}{dx} \left(1\right) \] \[\Rightarrow \cos(x)-\sin(y)y' = 0 \] \[\Rightarrow \sin(y)y' = \cos(x) \] \[\Rightarrow y' = \frac{\cos(x)}{\sin(y)} \]

ce qui conclut le calcul.

Autres calculatrices dérivées utiles

trouver la dérivée des fonctions simples et élémentaires est la pierre angulaire du processus de recherche des dérivées de fonctions plus compliquées, via l'utilisation de la méthode bien connue règles de différenciation .

Dans ce contexte, de base fonctions trigonométriques peuvent être considérées comme des fonctions élémentaires dont la dérivée peut être calculée à l'aide de bornes, via sa définition même. Parmi les fonctions élémentaires les plus utiles, nous avons polynômes et les fonctions rationnelles.