En savoir plus sur cette calculatrice de trigonométrie

Cette calculatrice de trigonométrie vous permettra d'évaluer toute expression trigonométrique que vous fournirez. Assurez-vous que vous fournissez une expression trigonométrique valide. Il peut s'agir d'une expression directe, comme cos(pi/2), ou d'une expression qui n'est pas entièrement simplifiée, comme sin(1/3*pi+3/4*pi).

Vous pouvez également fournir une fonction trigonométrique telle que sin(1/3*pi x +3/4*pi + x) et cette calculatrice analysera et, si possible, fournira la période, la fréquence, etc. correspondantes, ainsi que ses graphique .

Une fois qu'une expression trigonométrique valide a été fournie, il vous suffit de cliquer sur "Calculer" et toutes les étapes du calcul vous seront présentées.

expressions trigonométriques sont tout à fait nécessaires, surtout lorsque vous la résolution de triangles . Habituellement, il est simple de réduire tout calcul de trigonométrie au calcul de quelques angles notables pour le cosinus et sine .

Comment faire des calculs de trigonométrie ?

Effectuer un calcul trigonométrique peut être une tâche très générale et vaste, qui peut avoir des stratégies spécifiques qui fonctionnent mieux en fonction du calcul trigonométrique spécifique que vous devez effectuer et des fonctions trigonométriques impliquées, mais il existe certaines stratégies générales qui peuvent vous être utiles.

Quelles sont les étapes d'un calcul de trigonométrie ?

• Étape 1 : Identifiez clairement l'expression trigonométrique que vous voulez calculer, et simplifiez les nombres et la fraction autant que possible. Par exemple, si vous avez cos(1+1/2), vous remarquerez d'abord que 1+1/2 = 3/2, donc vous avez besoin en fait de cos(3/2)
• Étape 2 : Une fois les fractions et les nombres simples possibles regroupés et exploités si possible, déterminez s'il existe des fonctions trigonométriques autres que le sinus et le cosinus. Si c'est le cas, exprimez tout en termes de sinus et de cosinus
• Étape 3 : Passez maintenant en revue toutes les parties, qui ne concernent plus que les sinus et les cosinus et évaluer s'il existe des angles notables impliquant des multiples ou des fractions de π
• Étape 4 : évaluer directement ces expressions avec notable angles qui peuvent être simplifiées. Ceux qui ne peuvent pas être simplifiés directement (s'il y en a) sont laissés tels quels, ou fournissent une valeur approximative ( valeur arrondie ) d'entre eux

Il est d'usage de les laisser tels quels expressions qui n'ont pas de simplifications simples et connues. Par exemple, cos(1/4) n'a pas de réduction simple, donc on le laisse typiquement tel quel. Mais par exemple, cos(π/3) = 1/2, donc ces réductions simples sont évidemment effectuées

Calculatrice de trigonométrie avec étapes

L'avantage de cette calculatrice est qu'il vous montrera toutes les étapes pertinentes du processus. Le processus est simple : il s'agit simplifier les expressions qui n'impliquent que des nombres, des fractions et des expressions numériques globales directement évaluables.

Ensuite, et seulement ensuite, vous devez vous lancer dans le calcul de la trigonométrie, afin de clarifier les choses autant que possible avant de tenter tout calcul de trigonométrie.

Avantages de l'utilisation d'une application de calcul trigonométrique

Vous pouvez penser, oh bien, je connais assez bien mes fonctions trigonométriques pour les angles notables de base, donc je n'ai pas besoin d'une application de calculatrice trigonométrique. C'est peut-être le cas, mais vous pouvez hésiter un peu lorsqu'on vous présente quelque chose comme \(\sin\left(\displaystyle\frac{345}{11}\pi\right)\)....pouvez-vous le simplifier ? Est-ce un angle notable ?

C'est vraiment une bonne chose d'essayer de résoudre les choses à la main, et d'exercer sa mémoire trigonométrique, mais un application de calculatrice trigonométrique peut vous aider au moins à vérifier vos réponses.

Exemple : calcul de trigonométrie

Calculez l'expression trigonométrique : \(\sin\left(\frac{5}{4}\pi\right)\)

Solution: L'expression trigonométrique suivante a été fournie pour être calculée :

\[ \sin\left(\frac{5\pi}{4}\right)\]

En inspectant l'expression trigonométrique donnée, nous pouvons trouver un angle notable, qui est \(\sin\left(\frac{5\pi{}}{4}\right)\).

▹ Pour l'angle \(\frac{5\pi{}}{4}\) on obtient graphiquement :

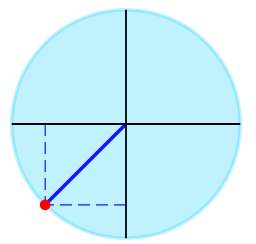
L'expression trigonométrique donnée peut être simplifiée comme suit :

Conclusion : Nous concluons que \(\displaystyle \sin\left(\frac{5\pi}{4}\right) = -\frac{1}{2}\sqrt{2} \approx -0.7071\).

Exemple : utilisation de la calculatrice de trigonométrie

Réduire : \(\displaystyle \cos\left(\frac{1}{3} + \frac{5}{4}\right)\)

Solution: Maintenant, nous devons travailler sur :

\[ \cos\left(\frac{1}{3}+\frac{5}{4}\right)\]

Ce terme trigonométrique peut être simplifié comme suit :

Conclusion : Il est conclu que \(\displaystyle \cos\left(\frac{1}{3}+\frac{5}{4}\right) = \cos\left(\frac{19}{12}\right) \approx -0.0125\).

Exemple : simplification de trigonométrie

Calculez \( \sin\left(\frac{2}{3} \times \frac{6}{5} \pi\right)+ \frac{2}{5}\cdot \cos(\frac{\pi}{4}) \).

Solution: En inspectant l'expression trigonométrique donnée, nous pouvons trouver un angle notable, qui est \(\cos\left(\frac{\pi{}}{4}\right)\).

▹ Pour l'angle \(\frac{\pi{}}{4}\) on obtient graphiquement :

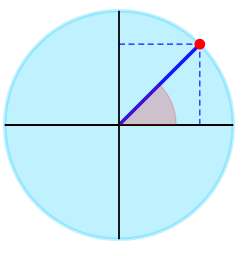
L'expression trigonométrique donnée peut être simplifiée comme suit :

Conclusion : Nous concluons que \(\displaystyle \sin\left(\frac{2}{3}\cdot\frac{6}{5}\pi\right)+\frac{2}{5}\cos\left(\frac{\pi}{4}\right) = \frac{1}{5}\sqrt{2}+\frac{1}{4}\sqrt{-2\sqrt{5}+10} \approx 0.8706\).

Plus de calculatrices de géométrie

Le travail avec les fonctions trigonométriques est étroitement lié au travail avec les triangles, donc quand vous travaillez avec un calculatrice de triangle vous trouverez beaucoup de calculs de trigonométrie.