À propos de cette calculatrice de péché

Le Présent calculatrice de sin vous fournira les deux éléments suivants : vous pouvez fournir une expression numérique telle que sin(pi/4), auquel cas la calculatrice la simplifiera et donnera une valeur numérique approximative si nécessaire. De même, si vous fournissez une fonction sin comme sin(3x+1), la calculatrice la représentera graphiquement.

Ensuite, la procédure est simple : une fois que vous avez fourni le expression du péché vous voulez calculer, il vous suffit de cliquer sur le bouton "Calculer" qui se trouve sous le formulaire pour obtenir les étapes de la solution.

Sine, ainsi que cosinus sont deux pierres angulaires de la trigonométrie. Vous verrez le sinus et le cosinus un peu partout lorsque vous vous rendrez compte qu'il s'agit d'une question de trigonométrie résolution de triangles par exemple, mais aussi dans des domaines comme la physique.

Comment calcule-t-on le péché ?

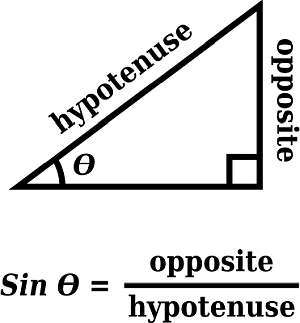
Le sin est l'un des éléments de base de la géométrie et de la trigonométrie. Le sin est une quantité qui peut être calculée pour les angles dans le contexte d'un triangle droit. Lorsque l'un des angles d'un triangle droit n'est pas l'angle de 90°, le sinus est calculé _o un, vous pouvez trouver le côté opposé et le côté adjacent .

La formule du sin est donc la suivante

\[\sin \theta = \frac{\text{Opposite Side} }{ \text{Hypothenuse} }\]

À quoi correspond le péché ?

Le sin est une grandeur sans dimension qui mesure l'importance de l'inclinaison d'un angle par rapport à la référence horizontale, où le côté adjacent est assis.

Lorsque sin est nul, l'angle est nul, il n'y a donc pas d'ouverture. L'ouverture maximale de l'angle se produit lorsque sin = 1, ce qui se produit à 90 _o .

Qu'est-ce que le péché de 1 ?

Cette question peut sembler innocente, mais elle est souvent source de confusion. En mathématiques, toutes les fonctions trigonométriques sont mesurées par défaut en radians. Mais pour une raison ou une autre, les radians ne sont pas bien connus ou trop populaires parmi les étudiants, qui préfèrent utiliser les degrés comme mesure, parce que c'est tout simplement plus familier.

Les élèves connaissent bien les angles notables en degrés comme 90 _o étant l'angle droit, et 360 _o étant le cercle complet. Vous pouvez utiliser cette calculatrice de degrés en radian pour passer d'un système à l'autre.

Ainsi, la réponse correcte à la question de savoir ce qu'est sin(1) est que sin(1) est approximativement 0,841471, lorsque l'angle 1 est supposé être exprimé en radians. Maintenant, sin(1) est approximativement 0,017452 lorsque l'angle 1 est supposé être exprimé en degrés. Il convient donc d'être extrêmement prudent lorsqu'il s'agit d'angles.

Quel est le sinus par rapport à la valeur négative de 1 ?

Une autre question dont la réponse est formellement simple, mais qui dépend parfois de la convention utilisée. Le sinus jusqu'à la valeur négative de 1 doit être précisé, car le sinus est une fonction. Vous pouvez donc faire sin(1), qui est un nombre, et sin(1) jusqu'à la valeur négative de 1, qui est l'inverse de sin(1), ce qui donne 1/sin(1), qui est un nombre.

Souvent, cependant, le sinus à la valeur négative de 1 est utilisé pour désigner la "fonction inverse du sinus", qui est connue sous le nom de fonction arcsin, ou parfois certaines personnes aiment utiliser la nomenclature \(sin^{-1}(x)\).

Puis-je utiliser une calculatrice scientifique pour calculer le sin

En effet, vous pouvez le faire, mais l'un des avantages de l'utilisation de cette méthode est qu'elle permet de réduire les coûts calculatrice de sin est que les étapes sont indiquées en même temps que le résultat. La plupart des calculatrices n'affichent que la réponse finale.

Comment utiliser une calculatrice de sinus ?

L'idée principale d'une calculatrice de sin est d'évaluer les expressions de sin que vous fournissez. Certains angles remarquables, généralement des multiples ou des fractions de \(\pi\), donnent des résultats simples, entiers ou fractionnaires lors du calcul de leur sin, il est donc judicieux d'utiliser une calculatrice d'expressions de sin pour vous aider.

Il n'est pas facile de se souvenir de tous les calculs de sin pour TOUS les angles notables, et vous finirez par travailler avec un triangle, en essayant d'obtenir la réponse manuellement, et une calculatrice sera utile pour vérifier ce que vous obtenez manuellement.

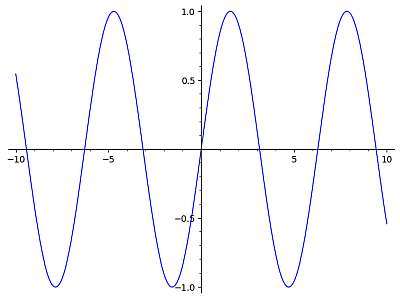
Vous pouvez également introduire dans la calculatrice une fonction sin, comme sin(pi x), et au lieu d'évaluer quelques points, cette calculatrice vous donnera le graphique correspondant

Quelles sont les étapes de l'utilisation d'une calculatrice de sinus ?

• Étape 1 : Identifiez l'expression de sin que vous voulez calculer
• Étape 2 : Tapez l'expression dans la case correspondante. Vous n'avez pas besoin de pré-simplifier, la calculatrice le fera pour vous
• Étape 3 : La calculatrice vérifie s'il s'agit d'une expression qui peut être évaluée, auquel cas elle se réduit à ses termes les plus simples
• Étape 4 : Si sin reste dans l'expression parce qu'elle n'a pas pu être simplifiée davantage, comme sin(3/4), la calculatrice vous donnera une valeur numérique approximative
• Étape 5 : Si une fonction sin est fournie à la place, un graphique sera fourni

Nous n'insisterons jamais assez sur l'importance de calculer correctement les opérations impliquant le sinus, car celles-ci apparaissent littéralement partout.

Formule du sin et du cos

Le sinus et le cosinus sont deux cousins très proches, voire des sœurs. Il existe entre eux une relation étroite, exprimée par la formule suivante :

\[\displaystyle \sin\left(\frac{\pi}{2} - x \right) = \cos(x) \]

Une autre formule qui relie initialement le sinus et le cosinus est la suivante :

\[\displaystyle \sin^2(x) + \cos^2(x) = 1 \]

Pourquoi le péché est-il si important ?

Les sinus sont importants car, avec les cosinus, ils sont au centre et au cœur de la construction d'un cercle. Et les cercles abritent de nombreuses autres constructions, comme les triangles, etc.

Le sinus et le cosinus finissent donc par s'entremêler dans chaque construction géométrique.

Exemple : calculatrice de sinus

Calculez l'expression sinusoïdale suivante : \(\sin\left(\frac{\pi}{3}\right)\)

Solution : L'expression trigonométrique suivante a été fournie pour être calculée :

\[ \sin\left(\frac{\pi}{3}\right)\]

En examinant l'expression trigonométrique donnée, nous pouvons trouver un angle notable, qui est \(\sin\left(\frac{\pi{}}{3}\right)\).

▹ Pour l'angle \(\frac{\pi{}}{3}\) on obtient graphiquement :

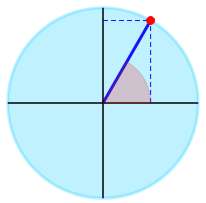
L'expression trigonométrique donnée peut être simplifiée comme suit :

Conclusion : Nous concluons que \(\displaystyle \sin\left(\frac{\pi}{3}\right) = \frac{1}{2}\sqrt{3} \approx 0.866\).

Exemple : autres calculs de sinus

Calculez ce qui suit : \( \sin\left(\frac{5}{4}\right) \)

Solution : L'expression trigonométrique suivante a été fournie pour être calculée :

\[ \sin\left(\frac{5}{4}\right)\]

mais cette expression trigonométrique ne peut pas être simplifiée davantage.

Conclusion : La fonction passée ne peut pas être simplifiée, et nous obtenons qu'approximativement \(\displaystyle \sin\left(\frac{5}{4}\right) \approx 0.949\).

Exemple : fonction sin

Calculer \( \sin(3x + 1) \).

Solution : Nous devons travailler avec la fonction trigonométrique suivante

\[f(x) = \sin\left(3x+1\right)\]

Sur la base de l'argument de la fonction trigonométrique qui a été transmis, la fréquence et la période sont calculées comme suit :

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{3} \\\\ \\\\ & \approx & 2.0944 \end{array}\]

et aussi

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{3}{2\pi} \\\\ \\\\ & \approx & 0.4775 \end{array}\]

En se basant sur la fonction trigonométrique fournie, \(f(x) = \sin\left(3x+1\right)\), on obtient que :

" L'amplitude dans ce cas est \(A = 1\).

" Le déphasage est égal à \(\displaystyle\frac{-1}{3} = -0.3333\).

" Le décalage vertical est égal à \( 0\).

En résumé, les résultats suivants ont été obtenus pour la fonction trigonométrique donnée

• Période = \(2.0944\)
• Fréquence = #XYZA
• Amplitude = \(1\)
• Décalage de phase = \(-0.3333\)
• Décalage vertical = \(\displaystyle 0\)

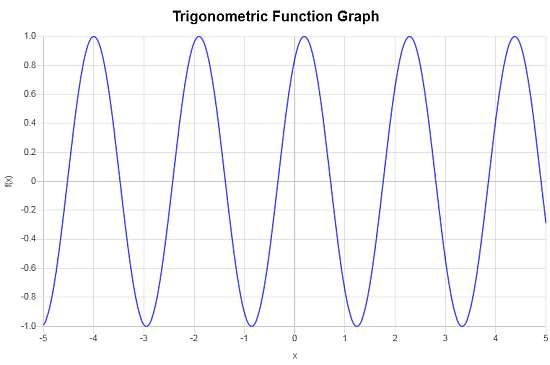
Voici le graphique correspondant

Plus de calculatrices trigonométriques

La trigonométrie réunit tous ces concepts, y compris cercles et triangles, et le sin et le cos sont au cœur même de la question.

Traiter avec expressions trigonométriques est une autre compétence cruciale qu'il est très important d'acquérir.