Radians en degrés
Instructions: Utilisez cette calculatrice de radians en degrés avec des étapes pour convertir un angle en radians en degrés. Tout ce que vous avez à faire est de taper l'angle en radians, et la calculatrice vous montrera comment le convertir en degrés, en montrant toutes les étapes:
En savoir plus sur la conversion des radians en degrés
Que sont les radians et pourquoi voulons-nous les convertir en degrés? En fin de compte, toutes les mesures d'angle sont arbitraires et sont liées à la taille d'une ouverture de deux rayons avec une ouverture d'origine commune. En effet, les angles se réfèrent à une mesure de l'ouverture entre les segments de ligne par rapport au cercle
Quels sont les différents référentiels pour mesurer les angles?
Lorsque nous mesurons un angle en degrés, un angle de 360 o correspond à l'ouverture complète d'un cercle. Tous les autres angles mesurés en degrés seront proportionnels à la quantité d'ouverture associée à l'angle.
Par exemple, si l'ouverture de l'angle correspond à la moitié de l'ouverture du cercle, l'angle sera la moitié de ce qui est pour l'ouverture complète, c'est la moitié de 360 o , soit 180 o
Un autre système pour mesurer les angles radians système, qui utilise une approche différente, mais qui est pourtant le même principe. Dans ce cas, l'angle dépend de l'ouverture, mais cette ouverture est mesurée en fonction du nombre de rayons représentés par la longueur d'arc du segment dans le cercle qui est déterminée par l'angle correspondant.
Nous savons que l'ouverture complète du cercle a un périmètre de \(2\pi\), ce qui autrement dit indique que nous pouvons ajuster les rayons \(2\pi\) dans l'ouverture complète du cercle, et cela indique que l'ouverture complète du cercle correspond à \(2\pi\) radians.
Comment convertir des radians en degrés?
Alors, quelle est la formule pour convertir les radians en degrés? Si vous avez un angle qui est mesuré comme \(r\) en radians, l'angle en degrés \(d\) est calculé comme suit:
\[d = \frac{360 r}{2\pi} = \frac{180 r}{\pi} \]La formule ci-dessus s'applique que vous convertissiez des décimales ou des fractions de radians en degrés. Tout ce que vous avez à faire est de brancher le nombre de radians \(r\) dans la formule
Exemple 1: Convertit les radians \(\pi\) en degrés.
Solution: Tout ce que vous avez à faire est de brancher \(r\) dans la formule ci-dessus. Dans ce cas, \(r = \pi\) radians, donc nous obtenons
\[d = \frac{180 r}{\pi} = \frac{180 \cdot \pi}{\pi} = 180^{o} \] so then \(\pi\) radians corresponds to 180 o degrees.Exemple 2: Convertissez maintenant les radians \(\displaystyle \frac{3\pi}{4}\) en degrés.
Solution: Comme pour l'exemple précédent, nous devons brancher \(r\) dans la formule ci-dessus. Dans ce cas, \(\displaystyle r = \frac{3\pi}{4}\) radians, donc nous obtenons
\[d = \frac{180 r}{\pi} = \frac{180 \cdot \frac{3\pi}{4}}{\pi} = 135^{o} \] so then \(\displaystyle \frac{3\pi}{4}\) radians corresponds to 135 o degrees.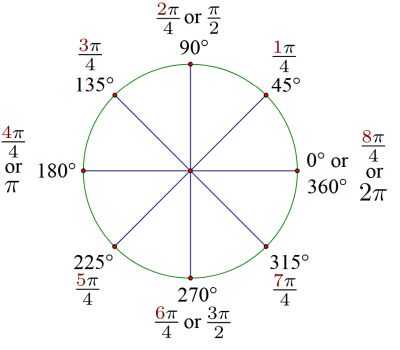
Comment utiliser Excel pour les conversions d'angle
Pour ceux d'entre vous qui travaillent avec Excel, vous pouvez utiliser la fonction "= DEGREES (r)" pour convertir un angle en radians en degrés.
Si au contraire vous pouvez convertir degrés de radians , vous devriez utiliser cet autre calculatrice .
Vous pouvez explorer d'autres calculatrices trigonométriques, telles que notre calculateur d'angle double , parmi beaucoup d'autres.
