Calculateur différentiel

Cette calculatrice vous permettra de calculer le différentiel d'une fonction que vous fournissez, à un point que vous fournissez, montrant toutes les étapes du processus.

La fonction que vous fournissez peut être n'importe quelle fonction différentiable valide comme f(x) = x^2 + 2x, ou f(x) = x^2*sin(x), pour ne citer que deux exemples.

Ensuite, lorsque vous avez fourni la fonction et le point pour le calcul différentiel, cliquez simplement sur "Calculer" afin d'obtenir toutes les étapes du processus affiché.

L'idée de Différentiel est étroitement avec celle de la tangente et Approximation Linéaire , car le différentiel mesure précisément la variation de y, le long de la Ligne Tangent au point donné.

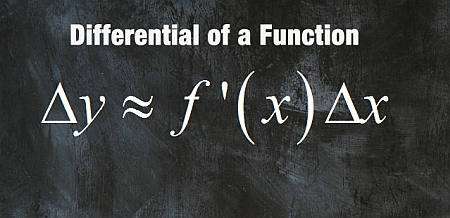
Qu'est-ce qu'un différentiel ?

Dans le calcul différentiel, l'idée est que les dérivées vous donnent des informations sur le taux de variation instantané d'une fonction à un point donné.

Le concept de différentiel utilise la taux de changement déterminée par la dérivée en un point donné \(x_0\) pour approximer le comportement de la fonction par sa Ligne Tangent .

La formule de la différentielle est basée sur l'idée que

\[\displaystyle \Delta y \approx f'(x_0) \Delta x \]

où \(\Delta y = y - f(x_0)\) et \(\Delta x = x - x_0\). Pour le différentiel \(dy\), on définit

\[\displaystyle dy = f'(x_0) dx \]

Cette définition (lâche) est basée sur l'idée que l'approximation linéaire et la fonction se rapprochent du même comportement lorsque \(x\) est suffisamment proche de \(x_0\).

Étapes pour calculer un différentiel

• Étape 1: Identifiez la fonction f(x) et le point x0 auquel vous voulez calculer la différentielle
• Étape 2: Calculez la dérivée f'(x) et évaluez-la en x0, vous obtenez donc f'(x0). Simplifiez-le, si nécessaire
• Étape 3: Utilisez la formule \(\displaystyle dy = f'(x_0) dx \)

Parfois, vous trouverez le différentiel écrit \(\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \), comme une forme d'indication que vous utiliserez le différentiel pour estimer les changements de y, mesurés par \(\Delta y\).

Calculatrice différentielle dy

Utilisant un calculateur différentiel peut vous faire gagner du temps avec le processus de calcul de la dérivée. L'idée du différentiel a toujours été étrange, dans le sens où elle semble être vaguement définie.

Bien qu'il existe un moyen de définir formellement les différentiels et leurs opérations (un sujet appelé formes différentielles), la plupart des mathématiciens ne voient pas de raison pour que les différentiels existent, car ils ne fournissent aucune nouvelle information que la dérivée ou l'approximation du premier ordre ne fournit pas.

Interprétation différentielle totale

L'application et l'interprétation les plus courantes de la différentielle sont lorsqu'elles sont utilisées dans son expression «finie»:

\[\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \]

où vous cherchez à estimer la variation de y, mesurée par \(\Delta y\), à partir de la variation de x, mesurée par \(\Delta x\) et la dérivée au point.

Parfois, ce \(\Delta y\) est appelé le variation totale ou différentiel total .

Conseils et astuces

N'oubliez pas que la différentielle peut être prise comme une définition théorique, \(\displaystyle dy = f'(x_0) dx \), qui indique la variation infinitésimale de y causée par une variation infinitésimale de x.

Il peut également être utilisé sous sa forme différentielle totale, dans laquelle vous avez

\[\displaystyle \Delta y \approx f'(x_0)(x-x_0)\]

qui vous indique une variation approximative de y, lorsqu'il s'agit d'un changement de x (de \(x_0\) à \(x\)).

Le centre de toute calculatrice algébrique commence par la puissance des nombres de base des fractions.

Exemple : calculateur différentiel

Considérez la fonction : \(f(x) = x^2\). Trouver son différentiel au point \(x_0 = 1\).

Solution: Dans le cas de ce premier exemple, on travaille avec la fonction \(\displaystyle f(x)=x^2\), pour laquelle il faut calculer sa différentielle au point \(x_0 = 1\).

La fonction est déjà simplifiée, nous pouvons donc procéder directement au calcul de sa dérivée :

Différentiel : La formule de la différentielle de la fonction \(\displaystyle f(x)=x^2\) au point \(x_0 = 1\) est :

\[dy = f'(x_0)(x - x_0) \]

On définit \(\displaystyle y_0 = f(x_0)\), donc insérer la valeur du point \(x_0 = 1\) dans la fonction conduit à :

\[y_0 = f(x_0) = f\left(1\right) = 1^2 = 1\]

De même, en branchant la valeur du point \(x_0 = 1\) à la dérivée calculée, on obtient :

\[f'(x_0) = f'\left(1\right) = 2\cdot 1 = 2 \]

Alors, nous insérons maintenant cette valeur dans la formule différentielle pour obtenir :

\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = 2\left(x-1\right) \]\[\Rightarrow dy = 2x-2 \]

Conclusion : Par conséquent, on trouve que la différentielle pour la fonction \(\displaystyle f(x)=x^2\) au point \(x_0 = 1\) est :

\[dy = 2x-2 \]

Exemple : calcul différentiel

Pour la fonction donnée : \(f(x) = x^3 + 3x^2 - 2\), trouver la différentielle au point \(x_0 = 2\).

Solution: Maintenant, la fonction dont nous avons besoin pour trouver la différentielle est \(\displaystyle f(x)=x^3+3x^2-2\),

Calcul Différentiel : Nous utilisons la formule suivante pour le différentiel que nous devons construire pour la fonction donnée \(\displaystyle f(x)=x^3+3x^2-2\), au point donné \(x_0 = \frac{1}{2}\) est :

\[dy = f'(x_0)(x - x_0) \]

Observez que \(\displaystyle y_0 = f(x_0)\), ce qui signifie qu'en évaluant la fonction en \(x_0 = \frac{1}{2}\) on trouve :

\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \left(\frac{1}{2}\right)^3+3\left(\frac{1}{2}\right)^2-2 = -\frac{9}{8}\]

Ensuite, on obtient la dérivée au point \(x_0 = \frac{1}{2}\) :

\[f'(x_0) = f'\left(\frac{1}{2}\right) = 3\left(\frac{1}{2}\right)^2+6\cdot \frac{1}{2} = \frac{15}{4} \]

Par conséquent, nous obtenons ce qui suit

\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(\frac{15}{4}\right)\left(x-\frac{1}{2}\right) \]\[\Rightarrow dy = \frac{15}{4}x-\frac{15}{8} \]

Conclusion : La conclusion finale est que la différentielle recherchée est donnée par :

\[dy = \frac{15}{4}x-\frac{15}{8} \]

Exemple différentiel

On nous donne la fonction : \(f(x) = \frac{\sin(x)}{x}\). Trouver son différentiel au point \(x_0 = \frac{\pi}{2}\).

Solution:

La fonction suivante a été fournie : \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), pour laquelle nous devons calculer sa différentielle au point \(x_0 = \frac{\pi}{2}\).

La fonction est déjà simplifiée, nous pouvons donc procéder directement au calcul de sa dérivée :

Calcutta : Il est maintenant temps de trouver la différentielle associée à \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), pour le point \(x_0 = \frac{\pi}{2}\) donné. La formule utilisée est :

\[dy = f'(x_0)(x - x_0) \]

On branche la valeur du point \(x_0 = \frac{\pi}{2}\) dans la dérivée calculée, ce qui conduit à :

\[f'(x_0) = f'\left(\frac{\pi}{2}\right) = \frac{\cos\left(\frac{\pi{}}{2}\right)}{\frac{\pi{}}{2}}-\frac{\sin\left(\frac{\pi{}}{2}\right)}{\left(\frac{\pi{}}{2}\right)^2} = -\frac{4}{\pi{}^2} \]

Donc, en utilisant la formule différentielle :

\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(-\frac{4}{\pi{}^2}\right)\left(x-\frac{1}{2}\pi{}\right) \]\[\Rightarrow dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]

Conclusion : Le différentiel correspondant est :

\[dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]

Autres calculatrices de différenciation

trouver des dérivés est sans aucun doute un élément clé de Calculus. Les dérivés fournissent les informations nécessaires pour comprendre les taux de changement de fonctions. car ceux-ci ont un lien intime.

Heureusement, trouver des dérivés est un processus systématique (pas nécessairement facile) si vous suivez des règles de différenciation . Les règles les plus utilisées sont les Règle Du Produit , Quotient Rule et Règle De La Chaîne .

Linéaire ou approximations du premier ordre tentent conceptuellement d'approximer une fonction par une ligne, au moins localement, et peuvent vous en dire beaucoup sur le comportement d'une fonction, à proximité d'un certain point.