Cómo funciona una calculadora de regresión logarítmica

Esta calculadora le permitirá estimar una regresión logarítmica para los datos de muestra que proporcione en la hoja de cálculo de entrada de datos correspondiente.

Cuando se proporcionan datos válidos (en este caso, la variable X sólo puede tomar valores positivos), después de hacer clic en "Calcular", obtendrá una ejecución de los pasos involucrados en el proceso, así como un diagrama de dispersión que mostrará la calidad del ajuste.

Tenga en cuenta que cuando los datos son dimensionalmente válidos, siempre se puede ejecutar una regresión logarítmica, pero eso no significa que los resultados serán de buena calidad, al menos en términos de ajuste.

Herramientas y calculadoras para la regresión logarítmica

Existen diferentes herramientas que puedes usar para estimar tu regresión logarítmica. En teoría, puedes hacerlo manualmente, usando una transformación logarítmica con una calculadora normal (incluso las que vienen con tu teléfono) y luego usar una ecuación auxiliar de mínimos cuadrados para encontrar el modelo logarítmico, que es

\[ Y = a + b \ln(X) + \varepsilon \]

Ciertamente, hacerlo a mano puede ser tedioso y propenso a errores, por decir lo menos. Por eso es una muy buena opción utilizar este Calculadora de regresión logarítmica , porque hace todo el trabajo por ti y te muestra todos los pasos

Hay otras herramientas, como aplicaciones para teléfonos móviles, que se supone que hacen todo tipo de regresiones, pero tendrás que probar y ver porque podría ser una situación imprecisa.

Pasos para ejecutar una regresión logarítmica

• Paso 1: Enumere claramente la variable independiente (X) y la variable dependiente (Y) y asegúrese de que ambas variables tengan el mismo tamaño de muestra
• Paso 2: Asegúrese de que sus valores de X sean positivos, de lo contrario no podrá ejecutar la regresión
• Paso 3: Construya una nueva variable independiente X* = ln(X) aplicando la transformación del logaritmo natural
• Etapa 4: Ahora ejecuta un análisis de regresión lineal regular para X* versus Y

Una cosa a tener en cuenta es que es totalmente recomendable utilizar una calculadora o un software para obtener estadísticas de diagnóstico que le ayudarán a evaluar si tiene sentido o no utilizar el modelo de regresión logarítmica .

Uso de excel frente a calculadoras de regresión logarítmica especializadas

Excel juega un papel importante al ayudarle a realizar análisis estadísticos básicos: le proporciona una interfaz limpia y probada para ejecutar pruebas básicas, incluido el cálculo de regresión logarítmica.

El principal problema de Excel es que no te proporciona los pasos de solución. Esto puede resultar de ayuda con la aparición de marcos de IA como Copilot, que probablemente dotarían a Excel de pasos descriptivos del cálculo.

Comprensión e interpretación de los resultados de la calculadora de regresión

Como cualquier otro Análisis de regresión , para el caso logarítmico no es diferente en el sentido de que deberá observar las estadísticas de ajuste del modelo, como la Estadísticas F para probar la significancia del modelo en su conjunto, y Estadísticas t para la significancia individual de los predictores .

Además, es probable que desees echar un vistazo a la variación y el error explicados, y la Coeficientes R^2 y R^2 ajustados , que le proporcionará estimaciones de la variación explicada de la variable dependiente por el modelo.

Ejemplos de regresión logarítmica

Considere las variables

X: 1, 2, 3, 4, 5

Y: 15, 25, 28, 29, 30

Estimar un modelo de regresión logarítmica.

Solución:

Se proporcionan los siguientes datos de las variables X e Y para construir un modelo de regresión logarítmica:

Incógnita	Y
1	15
2	25
3	28
4	29
5	30

La variable independiente que utilizaremos es el logaritmo natural de X, y la variable dependiente es Y. Para calcular los coeficientes de regresión para esta regresión auxiliar, se debe utilizar la siguiente tabla:

	Incógnita	Z = ln(X)	Y	\(Z \cdot Y\)	\(Z^2\)	\(Y^2\)
	1	0	15	0	0	225
	2	0.69	25	17.33	0.48	625
	3	1.1	28	30.76	1.21	784
	4	1.39	29	40.2	1.92	841
	5	1.61	30	48.28	2.59	900
Sum =	15	4.79	127	136.58	6.2	3375

Con base en la tabla anterior se calcula lo siguiente:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 4.787491742782}{ 5} = 0.957\]\[\bar Y = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 127}{ 5} = 25.4\]\[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 6.2 - 4.787^2/5 = 1.615\]\[\large SS_{YY} = \sum_{i=1}^{n} Y_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Y_i\right)^2 = 3375 - 127^2/5 = 149.2\]\[\large SS_{ZY} = \sum_{i=1}^{n} Z_i Y_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} Y_i\right) = 136.575 - 4.787 \times 127/5 = 14.973\]

Por lo tanto, en base a los cálculos anteriores, los coeficientes de regresión (la pendiente \(m\) y la intersección con el eje y \(n\)) se obtienen de la siguiente manera:

\[m = \frac{SS_{ZY}}{SS_{ZZ}} = \frac{ 14.973}{ 1.615} = 9.2685\] \[n = \bar Y - \bar Z \cdot m = 25.4 - 0.957 \times 9.2685 = 16.5254\]

Por lo tanto, encontramos que la ecuación de regresión es:

\[\text{ Y} = 16.5254 + 9.2685 \text{ Z}\]

Pero como la variable auxiliar \(Z = \ln(X)\), concluimos que la ecuación de regresión logarítmica es:

\[\text{ Y} = 16.5254 + 9.2685 \ln(X)\]

Por tanto, con base en la información proporcionada anteriormente, se obtienen los siguientes diagramas de dispersión y de regresión:

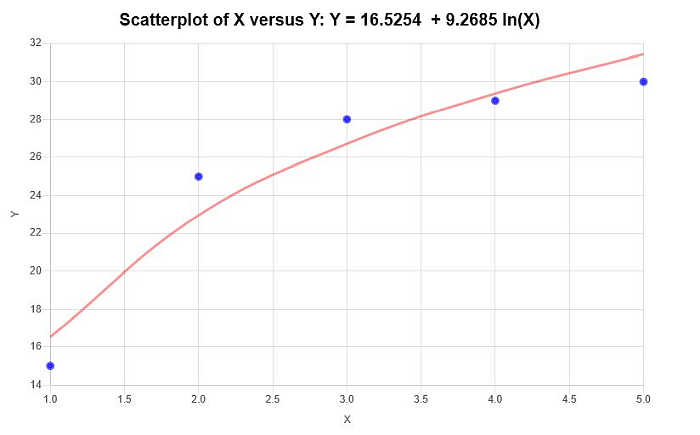
Más calculadoras de estadísticas

Usted también podría estar interesado en Calcular una regresión exponencial , o resolver las sutilezas de un Regresión polinomial , todos los cuales se aplican en diferentes contextos, en función del comportamiento de los datos de muestra observados.

Probablemente querrás construir un diagrama de dispersión para evaluar el comportamiento empírico de los datos y evaluar previamente si se aplica una regresión logarítmica en lugar de un tipo diferente de regresión.