Calculadora de coeficiente de determinación

La idea de la regresión lineal es poder predecir una variable dependiente a partir de una o más variables independientes. Para ello buscamos un modelo que se ajuste lo mejor posible a los datos.

Hay diferentes formas de evaluar la fuerza de una asociación lineal entre dos variables y esta calculadora de r cuadrado es una herramienta que se utiliza para evaluar eso.

Una medida de bondad de ajuste para un modelo de regresión lineal está representada por el coeficiente de determinación, o \(R^2\), y se utiliza ampliamente para evaluar la calidad de un modelo de regresión lineal.

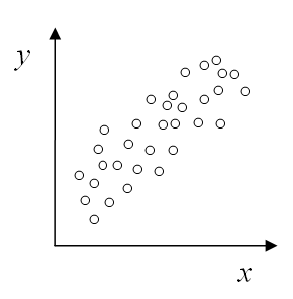
Por supuesto, no puedes usar R o R^2 solo, necesitarás hacer un diagrama de dispersión y observe que los datos siguen visualmente un patrón de línea recta.

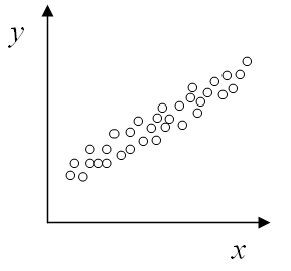
¿es esta calculadora de r cuadrado?

Sí, lo es. De hecho, coeficiente de determinación es otro nombre para R-Cuadrado , y se pueden usar indistintamente, especialmente para el caso de una variable dependiente (Y) y una variable independiente (X), es decir, en el caso de una Regresión lineal simple .

Para el caso de una regresión lineal múltiple donde hay más de una variable independiente (o predictor), las cosas son un poco más sutiles, como se suele llamar al coeficiente R cuadrado. coeficiente de determinación múltiple .

Además, en una regresión lineal múltiple, se sabe que el R cuadrado "infla" el porcentaje de variación explicado, y preferimos utilizar el coeficiente R cuadrado ajustado.

Por ejemplo, puedes usar este calculadora de coeficiente R cuadrado ajustado para obtenerlo directamente de datos de muestra, o puede obtener esta calculadora para obtenerlo de R cuadrado , si ya lo tienes. R-cuadrado.

¿cómo se calcula el coeficiente de determinación?

Muy a menudo, el coeficiente de determinación se calcula utilizando algún tipo de paquete de software estadístico. Pero utilizar la definición matemática real es útil para llegar a una interpretación importante de R-Squared.

Matemáticamente, el coeficiente de determinación se calcula como

\[ R^2 = \frac{SSR}{SST}\]

donde \(SSR\) representa la suma de cuadrados de la regresión y \(SST\) representa la suma total de cuadrados. Recordemos que la variación total (\(SST\)) se divide en variación explicada (\(SSR\)) y variación no explicada (\(SSE\)), como se muestra a continuación:

\[SST = SSR + SSE\]

¿qué representa el coeficiente de determinación?

Interpretación del coeficiente de determinación. : Según la forma en que se define, el coeficiente de determinación es simplemente la relación entre la variación explicada y la variación total. En otras palabras, el coeficiente de determinación representa la proporción (o porcentaje) de variación en la variable dependiente que se explica por la modelo de regresión lineal .

Por ejemplo, si el coeficiente de determinación es \(R^2 = 0.473\), ¿qué te dice eso? Indica que el 47,3% de la variación de la variable dependiente se explica por el correspondiente modelo de regresión lineal.

¿cómo se calcula la calculadora del coeficiente de determinación dado r?

Esa es una tarea sencilla: si tienes o te proporcionan el coeficiente de correlación \(r\), lo único que tienes que hacer es elevar ese número al cuadrado, esto para calcular \(r^2\), para obtener el coeficiente de determinación.

Calculadora de r cuadrado en excel

¿Puedes calcular R-cuadrado en Excel? La respuesta es: ¡por supuesto! Debe calcular el coeficiente de correlación \(r\) usando el comando "=CORREL()" y luego, usando la celda que contiene la correlación, diga "A1", cree una celda con la fórmula "=A1^2". para obtener r al cuadrado

Calculadora r

¿Están relacionadas la calculadora r y la calculadora r cuadrado? Generalmente lo son. La mayoría de las calculadoras de r cuadrado primero calculan el coeficiente de correlación y luego lo elevan al cuadrado para obtener r al cuadrado.

Puedes usar esta calculadora para calcular r directamente utilizando los datos de muestra proporcionados.