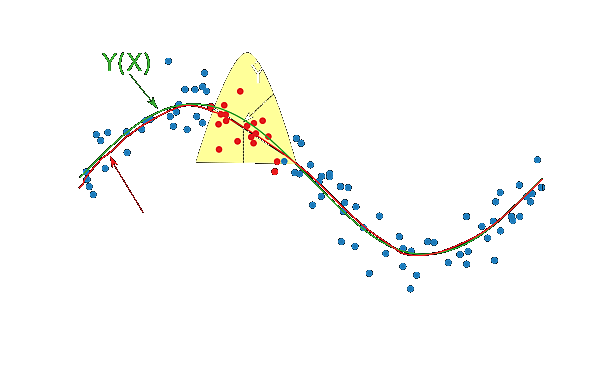
Calculadora de regresión polinomial
Instrucciones: Puede utilizar esta Calculadora de regresión lineal múltiple para estimar un modelo lineal proporcionando los valores de muestra para un predictor \((X)\) y sus potencias hasta un cierto orden, y una variable dependiente \((Y)\), mediante el siguiente formulario:
Calculadora de regresión polinomial
Más sobre esto Calculadora De Regresión Polinomial para que puedas tener una perspectiva más profunda de los resultados que te proporcionará esta calculadora.
La regresión polinómica es muy similar a la regresión lineal simple, solo que ahora se usa un predictor y un cierto número de sus potencias para predecir una variable dependiente \(Y\).
¿qué es el modelo de regresión polinómica?
Entonces, una de las grandes preguntas aquí es: ¿se puede escribir una ecuación de regresión polinómica? El modelo de regresión lineal polinomial se escribe como
\[ Y = \displaystyle \beta_0 + \beta_1 X + \beta_2 X^2 + ... + \beta_n X^n + \epsilon\]donde \(\epsilon\) es el término de error que tiene la propiedad de distribuirse normalmente con media 0 y varianza constante \(\epsilon ~ N(0, \sigma^2)\).
Después de proporcionar valores de muestra para el predictor \(X\) y la variable de respuesta \(Y\), se obtienen estimaciones de los coeficientes de pendiente de la población minimizando la suma total de errores al cuadrado. El modelo estimado se expresa como:
\[ \hat Y = \displaystyle \hat\beta_0 + \hat\beta_1 X + \hat\beta_2 X^2 + ... + \hat\beta_n X^n\]
¿cómo se calcula la regresión polinómica?
El procedimiento es el mismo que con la mayoría de los procedimientos de regresión: tiene una variable dependiente \(Y\) que desea predecir en términos de uno o más predictores.
En este caso, la variable independiente es \(X\) y los predictores son \(X\) junto con todas sus potencias enteras hasta un número entero \(n\), que es \(X, X^2, ...., X^n\)
¿es esta una calculadora de regresión polinomial con pasos?
Los pasos se muestran en el sentido de que las matrices involucradas que necesitan operación están claramente identificadas y las operaciones matriciales están claramente establecidas.
No sería factible mostrar cada paso algebraico del proceso en un cálculo matricial muy largo como los requeridos en este caso.

¿cómo se encuentra la regresión polinómica a mano?
En teoría, se podrían hacer los cálculos a mano, pero en este caso, dado que hay muchas variables involucradas, los cálculos incluyen operaciones matriciales, como invertir una matriz, lo cual es realmente engorroso de hacer a mano.
Otras calculadoras de regresión
La regresión es uno de los modelos más utilizados y versátiles en estadística, donde se utilizan uno o más predictores para predecir el valor de una variable dependiente de escala Y.
Cuando quieras usar solo un predictor, sin energía, puedes usar este calculadora de regresión lineal simple en cambio. O si tiene varios predictores, debe usar este Calculadora de regresión lineal múltiple .
Una de las principales características del modelo de regresión es que se supone que la variable dependiente es un intervalo. Hay muchos casos en los que nos gustaría estimar un modelo en el que la variable dependiente sea binaria (0 - 1). En esos casos, necesitamos usar un Regresión logística .