Más sobre este generador de gráficos cuadráticos

Esta calculadora de gráficos cuadráticos le permitirá generar el gráfico para cualquier función cuadrática que proporcione. Puede ser cualquier función cuadrática válida, por ejemplo, x^2 - 3x + 1/2, pero también puede proporcionar una función cuadrática que no esté simplificada, como x^2 - 3x - 4 - 1/2 x^2 - 1/5, siempre que sea una función cuadrática válida.

Una vez que proporcione una expresión cuadrática válida, puede hacer clic en el botón "Calcular" y el gráfico de la función se generará, mostrándole los pasos del cálculo de la vértice de la parábola y el Eje de simetria también .

Las funciones cuadráticas tienen un papel predominante en el Álgebra básica, ya que se utilizan con frecuencia en el contexto de la solución de ecuaciones cuadráticas y problemas de aplicación. Son esencialmente básicos. polinomios , que tienen muchas propiedades interesantes.

¿cómo graficar cuadráticas?

Hacer un gráfico cuadrático es simple, en el sentido de que sabes que TODAS las funciones cuadráticas tendrán la forma de una parábola. Pero, sin embargo, hay infinitas parábolas. Necesitamos saber un poco más para identificar LA parábola precisa que representa una función cuadrática dada.

Pasos para encontrar la gráfica de una función cuadrática

• Paso 1: Identifique claramente la función cuadrática dada y simplifique si es necesario
• Paso 2: Después de simplificar, identifica la función en la forma f(x) = ax² + bx + c. Observe que a no puede ser cero
• Paso 3: Si a > 0, sabes que la gráfica será una parábola que abre hacia arriba, mientras que si a < 0, sabes que la gráfica será una parábola que abre hacia abajo
• Paso 4: El eje de simetría está en x* = -b/(2a), que te indica el 'centro' de la parábola
• Paso 5: Note que x* = -b/(2a) es la coordenada x del vértice de la parábola, y y* = f(x*) = a(x*)² + b(x*) + c es la coordenada y del vértice

Eso debería ser suficiente para tener una idea clara sobre el gráfico cuadrático correspondiente. Un paso más sería trazar algunos puntos en el gráfico, eligiendo diferentes puntos en el eje x y encontrando su imagen correspondiente a través de la función, para ayudar en el proceso de encontrar el gráfico de la función .

La fórmula cuadrática

Es el Fórmula cuadrática relacionado con la gráfica de una función cuadrática? ¡Apuesta! Geométricamente hablando, al resolver la ecuación cuadrática

\[a x^2 + bx + c = 0 \]

obtienes las raíces de la ecuación cuadrática, y cuando las raíces son reales, representan los puntos donde la parábola cruza el eje x.

Un caso especial ocurre cuando las raíces son complejas, en cuyo caso la parábola no cruzará el eje x.

Tipos de gráficos cuadráticos

Como mencionamos antes, TODAS las funciones cuadráticas univariadas estarán representadas por parábolas, pero dependiendo de si a > 0 o a < 0, las parábolas se abrirán hacia arriba o hacia abajo respectivamente.

Otra distinción de los tipos de parábolas podría ser para las que están "centradas" (esto es, las vértice es un origen), y los que no lo son.

Ejemplo: gráfico cuadrático

Construya la gráfica de : \(f(x) = \frac{1}{3}x^2 +2x - 3\)

Solución:

Necesitamos graficar la función cuadrática provista \(f(x) = \displaystyle \frac{1}{3}x^2+2x-3\). Además, se calcularán las coordenadas del vértice.

Para una función cuadrática de la forma \(f(x) = a x^2 + bx + c\), la coordenada x del vértice se calcula usando la siguiente fórmula:

\[x_V = \displaystyle -\frac{b}{2a}\]

En este caso, tenemos que la función para la que necesitamos encontrar el vértice es \(f(x) = \displaystyle \frac{1}{3}x^2+2x-3\), lo que implica que los coeficientes correspondientes son:

\[a = \frac{1}{3}\] \[b = 2\] \[c = -3\]

Reemplazando los valores conocidos de \(a\) y \(b\) en la fórmula para la coordenada x del vértice, obtenemos:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{2}{2 \cdot \frac{1}{3}} = -3\]

Ahora, necesitamos reemplazar el valor de \(x_V = \displaystyle -3\) en la función cuadrática, por lo que obtenemos:

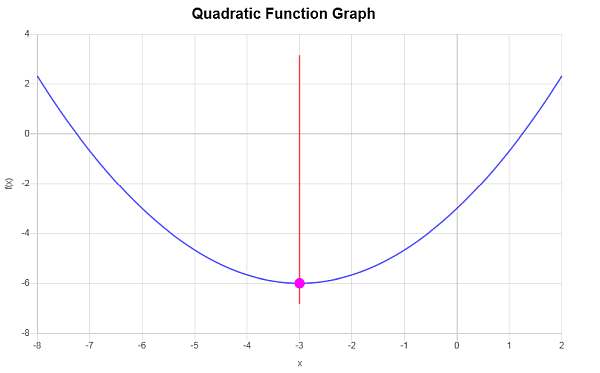
\[y_V = f(x_V)\] \[ = \frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=\frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=9\cdot\frac{1}{3}-6-3=3-6-3=-6\]

Por lo tanto, la coordenada x del vértice es \(x_V = \displaystyle -3\), y la coordenada y del vértice es \(y_V = \displaystyle -6\). Esto indica que el punto que representa el vértice es \( \displaystyle \left(-3, -6\right)\).

De forma gráfica se obtiene lo siguiente:

Ejemplo: gráfico cuadrático

Gráfico: \(f(x) = \frac{4}{3}x^2 +3x - 2\), ¿qué tipo de gráfico cuadrático es este?

Solución: En este caso, tenemos que la función para la que necesitamos encontrar el vértice es \(f(x) = \displaystyle \frac{4}{3}x^2+3x-2\), lo que implica que los coeficientes correspondientes son:

\[a = \frac{4}{3}\] \[b = 3\] \[c = -2\]

Reemplazando los valores conocidos de \(a\) y \(b\) en la fórmula para la coordenada x del vértice, obtenemos:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot \frac{4}{3}} = -\frac{9}{8}\]

Ahora, necesitamos reemplazar el valor de \(x_V = \displaystyle -\frac{9}{8}\) en la función cuadrática, por lo que obtenemos:

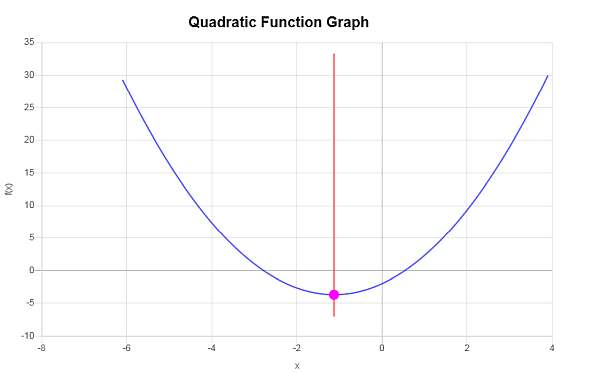
\[y_V = f(x_V)\] \[ = \frac{4}{3}\cdot \left(-\frac{9}{8}\right)^2+3\cdot \left(-\frac{9}{8}\right)-2=\frac{4}{3}\cdot\frac{81}{64}+3\cdot \left(-\frac{9}{8}\right)-2=\frac{27}{16}-\frac{27}{8}-2=-\frac{59}{16}\]

Por lo tanto, la coordenada x del vértice es \(x_V = \displaystyle -\frac{9}{8}\), y la coordenada y del vértice es \(y_V = \displaystyle -\frac{59}{16}\). Esto indica que el punto que representa el vértice es \( \displaystyle \left(-\frac{9}{8}, -\frac{59}{16}\right)\).

De forma gráfica se obtiene lo siguiente:

Más calculadoras cuadráticas

La mayoría de las aplicaciones en Álgebra básica se basan en resolver algún tipo de Ecuación cuadrática , por lo que tiene un fuerte propósito pedagógico para aprender sobre el mismo.

El Fórmula cuadrática es uno de los objetos de enseñanza más notorios en Matemáticas. No es que no existan ecuaciones cúbicas o cuárticas, es que ecuaciones cuadráticas son los que podemos explicar fácilmente.