Calculadora de ecuaciones cuadráticas

Esta calculadora te permitirá calcular una ecuación cuadrática que usted proporciona, mostrando todos los pasos. Todo lo que necesita hacer es proporcionar una ecuación cuadrática válida.

Podría ser algo que ya está simplificado y listo para resolver como x ^ 2 + 3x + 5 = 0, puede proporcionar algo que no se simplifique fácilmente como 3x ^ 2 - 4x + 5/3 = x ^ 2 + 1/3x - 1, por ejemplo.

Una vez que proporcione una ecuación cuadrática válida, todo lo que necesita hacer es hacer clic en "Calcular", y se le proporcionarán todos los pasos del proceso para calcular el raíces de la ecuación cuadrática que se proporciona.

Por lo general, usarás la fórmula cuadrática para calcular ecuaciones cuadráticas, pero esa no es la única forma, como veremos en las siguientes secciones.

¿cómo calcular una ecuación cuadrática?

Hay varias estrategias para resolver ecuaciones cuadráticas. El más utilizado es el uso de la Fórmula cuadrática . Además, puedes resolver por completar cuadrados , o puedes resolver por factorización cuadrática .

¿cuáles son los pasos para calcular ecuaciones cuadráticas usando la fórmula cuadrática?

• Paso 1: Identifique la ecuación cuadrática que desea calcular
• Paso 2: asegúrese de que la ecuación esté completamente simplificada; de lo contrario, continúe con la simplificación hasta que tenga una ecuación de la forma ax² + bx + c = 0
• Paso 3: Después de reducir la ecuación a su forma simplificada, puede usar la fórmula cuadrática: \(x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

Posiblemente, usar la fórmula de la ecuación cuadrática es la forma más práctica de encontrar las raíces de una ecuación cuadrática, pero hay otras razones por las que usaría otros métodos.

¿cómo resolver una ecuación cuadrática completando cuadrados?

La segunda forma más común de resolver una ecuación cuadrática es usando la técnica de completar cuadrados . Realmente no existe una fórmula para completar cuadrados (aunque técnicamente existe una, basada en las soluciones de la ecuación cuadrática), sino más bien un proceso.

¿cuáles son los pasos para completar cuadrados?

• Paso 1: identifica la ecuación cuadrática que quieres resolver
• Paso 2: debe asegurarse de que la ecuación esté completamente simplificada y de que tenga una ecuación de la forma ax² + bx + c = 0
• Paso 3: suma y resta un término adecuado (en este caso, (b/(2a))² para forzar los términos del cuadrado de un binomio

La idea de forzar la aparición de un término de la forma (x + "algo)², que es el objetivo final de completar cuadrados.

¿por qué usarías ecuaciones cuadráticas?

Las ecuaciones cuadráticas aparecen constantemente en las aplicaciones de álgebra son problemas de palabras. Resolver ecuaciones cuadráticas es una habilidad básica básica que debes adquirir.

Luego, en campos como Cálculo, al calcular problemas de maximización y minimización, deberá estar bien familiarizado con todos los tipos de ecuaciones cuadráticas.

Ejemplo: resolver una ecuación cuadrática

Resuelve la siguiente ecuación cuadrática usando la fórmula \(4x^2 + \frac{4}{3}x + 2 = 0\)

Solución: Necesitamos resolver la siguiente ecuación cuadrática dada \(\displaystyle 4x^2+\frac{4}{3}x+2=0\).

Para una ecuación cuadrática de la forma \(a x^2 + bx + c = 0\), las raíces se calculan usando la siguiente fórmula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

En este caso, tenemos que la ecuación que debemos resolver es \(\displaystyle 4x^2+\frac{4}{3}x+2 = 0\), lo que implica que los coeficientes correspondientes son:

\[a = 4\] \[b = \frac{4}{3}\] \[c = 2\]

Primero, calcularemos el discriminante para evaluar la naturaleza de las raíces. La discriminación se calcula como:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{4}{3}\right)^2 - 4 \cdot \left(4\right)\cdot \left(2\right) = -\frac{272}{9}\]

Dado que en este caso obtenemos que el discriminante es \(\Delta = \displaystyle -\frac{272}{9} < 0\), que es negativo, sabemos que la ecuación dada tiene dos raíces complejas conjugadas diferentes.

Ahora, reemplazando estos valores en la fórmula de las raíces obtenemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{\left(\frac{4}{3}\right)^2-4\left(4\right)\left(2\right)}}{2\cdot 4} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{-\frac{272}{9}}}{8}\]

entonces, encontramos que:

\[\displaystyle x_1 = \frac{-\frac{4}{3} - i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\] \[\displaystyle x_2 = \frac{-\frac{4}{3} + i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\]

Por lo tanto, la ecuación dada \(\displaystyle 4x^2+\frac{4}{3}x+2=0\) tiene dos raíces complejas conjugadas diferentes, que son \(x_1 = \displaystyle -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\) y \(x_2 = \displaystyle -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\).

Gráficamente:

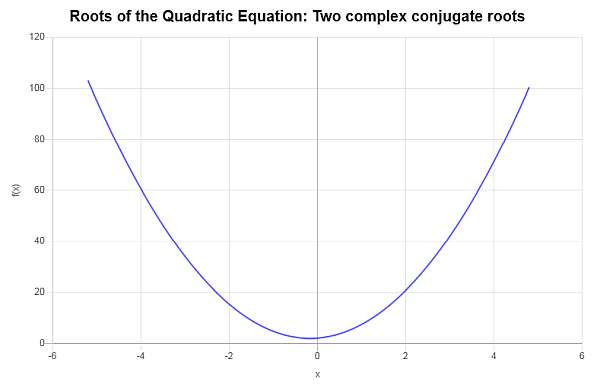
Ejemplo: raíz de una ecuación cuadrática

Encuentra las raíces de la siguiente ecuación cuadrática completando cuadrados \(2x^2 + \frac{1}{3}x + \frac{1}{72} = 0\)

Solución: En este caso, tenemos que la ecuación que debemos resolver es \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72} = 0\), lo que implica que los coeficientes correspondientes son:

\[a = 2\] \[b = \frac{1}{3}\] \[c = \frac{1}{72}\]

La discriminación se calcula como:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{1}{3}\right)^2 - 4 \cdot \left(2\right)\cdot \left(\frac{1}{72}\right) = 0\]

Como en este caso obtenemos que el discriminante es \(\Delta = \displaystyle 0 = 0\), que es cero, sabemos que la ecuación tiene una sola raíz real.

Ahora, reemplazando estos valores en la fórmula de las raíces obtenemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{\left(\frac{1}{3}\right)^2-4\left(2\right)\left(\frac{1}{72}\right)}}{2\cdot 2} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{0}}{4}\]

entonces, encontramos que:

\[x = \displaystyle \frac{-\frac{1}{3}}{4} = \displaystyle -\frac{1}{12}\]

Por lo tanto, la ecuación dada \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72}=0\) tiene solo una raíz real, que es \(x = \displaystyle -\frac{1}{12}\).

Gráficamente:

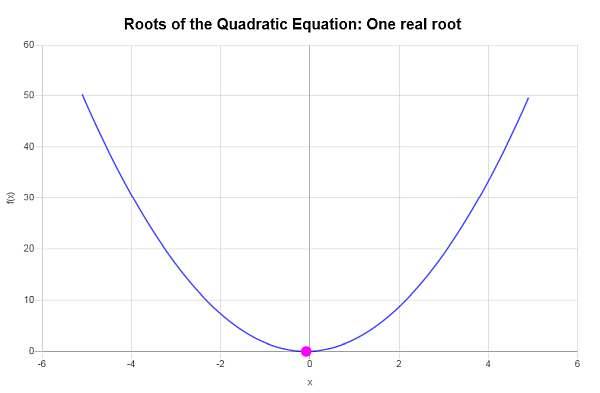
Ejemplo: cálculo de raíces de ecuaciones

Resuelve lo siguiente: \(3x^2 + \frac{2}{3}x - \frac{4}{3} = 0\)

Solución: Para este ejemplo la ecuación que necesitamos resolver es \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3} = 0\), entonces los coeficientes correspondientes son:

\[a = 3\] \[b = \frac{2}{3}\] \[c = -\frac{4}{3}\]

En este caso, la discriminación se calcula como:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{2}{3}\right)^2 - 4 \cdot \left(3\right)\cdot \left(-\frac{4}{3}\right) = \frac{148}{9}\]

Como el discriminante es \(\Delta = \displaystyle \frac{148}{9} > 0\), que es positivo, sabemos que la ecuación tendrá dos raíces reales diferentes.

Ahora, reemplazando estos valores en la fórmula de las raíces obtenemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\left(\frac{2}{3}\right)^2-4\left(3\right)\left(-\frac{4}{3}\right)}}{2\cdot 3} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\frac{148}{9}}}{6}\]

entonces, encontramos que:

\[ x_1 = -\frac{\frac{2}{3}}{6}-\frac{1}{6}\sqrt{\frac{148}{9}}=-\frac{1}{9}\sqrt{37}-\frac{1}{9} \] \[x_2 = -\frac{\frac{2}{3}}{6}+\frac{1}{6}\sqrt{\frac{148}{9}}=\frac{1}{9}\sqrt{37}-\frac{1}{9}\]

Por lo tanto, la ecuación dada \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3}=0\) tiene dos raíces reales diferentes, que son \(x_1 = \displaystyle -\frac{1}{9}\sqrt{37}-\frac{1}{9}\) y \(x_2 = \displaystyle \frac{1}{9}\sqrt{37}-\frac{1}{9}\).

Gráficamente:

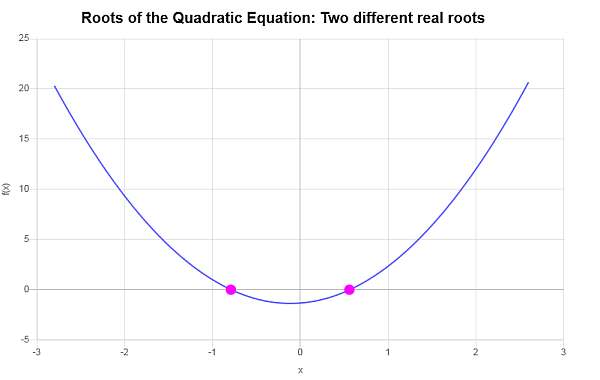
Otras calculadoras cuadráticas útiles

Como hemos visto en este tutorial, completar cuadrados juega un papel fundamental en el cálculo de ecuaciones cuadráticas. Además, puedes usar este calculadora discriminante para evaluar la naturaleza de las raíces (dos raíces reales, una raíz real o dos raíces complejas) sin resolver la ecuación.

También puedes usar esto Calculadora de vértices para encontrar las coordenadas del vértice de una ecuación cuadrática, y hallar el eje de simetria de una parabola . También puedes explorar este factorización cuadrática herramienta para explorar otra forma de calcular ecuaciones cuadráticas.