Cálculo de la elasticidad precio de la demanda a partir de datos de muestra

Utilice esta calculadora para estimar la elasticidad precio de la demanda basándose en datos de muestra de precio y cantidad demandada que usted proporcione.

Deberá proporcionar datos de muestra válidos, en términos de que ambas muestras (precio y cantidad demandada) sean valores positivos. Una vez que haya pegado los datos en la hoja de cálculo, puede hacer clic en "Calcular" para obtener todos los pasos que se muestran.

Observe que este enfoque requiere que los datos sigan un patrón específico que se adapte a un modelo logarítmico-logarítmico, donde \(\ln(P)\) y \(\ln(Q)\) se utilizan como variables auxiliares para realizar un modelo de regresión lineal.

Cálculo de la elasticidad del precio a partir de datos de muestra

Para calcular la elasticidad del precio, necesitará estimar el siguiente modelo auxiliar:

\[\displaystyle \ln(Q) = a + b \ln(P) \]

Observe que esto corresponde a un modelo de regresión lineal regular en el que las variables originales precio y cantidad se transforman en logaritmos. Por eso, exigimos que ambas variables sean estrictamente positivas.

¿cuales son los pasos para calcular la elasticidad?

• Paso 1: Identifique los datos de muestra para las variables proporcionadas para el precio (P) y la cantidad (Q)
• Paso 2: Asegúrese de que ambas muestras tengan el tamaño de muestra adecuado y que AMBAS sean positivas, de lo contrario no podrá realizar el cálculo
• Paso 3: Transformar logaritmo en ambas variables: Calcular ln(X) y ln(Y)
• Etapa 4: Realice una regresión lineal auxiliar para las variables ln(X) y ln(Y), donde ln(X) es la variable independiente y ln(Y) es la variable dependiente
• Paso 5: El coeficiente de pendiente encontrado para esta regresión auxiliar es la elasticidad precio de la demanda para estos datos

El paso crucial entonces es la transformación logarítmica de los datos, que nos permite calcular la elasticidad en base a los resultados de una regresión lineal, lo que hace que los resultados encontrados sean altamente interpretables.

Comprender la elasticidad del precio

Por definición, la elasticidad del precio se define mediante la siguiente fórmula:

\[ \varepsilon = \displaystyle \frac{\% \Delta Q }{\% \Delta P} \]

Esto indica que, entre otras cosas, podemos predecir el cambio porcentual de la demanda de cantidad utilizando la siguiente expresión:

\[ \% \Delta Q = \varepsilon \cdot \% \Delta P \]

Esto indica que el cambio porcentual en Q es el mismo que el cambio porcentual en P multiplicado por la elasticidad. Es importante señalar que esta definición se aplica Puntualmente : es decir, la elasticidad no tiene por qué ser constante a lo largo de la curva de demanda, aunque puede serlo, y en esta calculadora se hace tal suposición.

Interpretación de los coeficientes de elasticidad de precios

Como vimos en la sección anterior, la elasticidad \(\varepsilon\) simplemente corresponde al coeficiente de pendiente de la regresión auxiliar transformada en logaritmo. Pero, además, tiene una interpretación de cambio marginal muy interesante:

• Por un cambio adicional del 1% en el precio, la cantidad demandada cambia en \(\varepsilon \%\)

Esto es precisamente lo que exige y lo que implica la fórmula de elasticidad. Observe que esta calculadora estima un modelo que supone que los datos siguen un patrón que conduce a una elasticidad constante, lo que no sucede en el caso de una función de demanda lineal, por ejemplo.

Factores que influyen en la elasticidad del precio

La elasticidad es un reflejo de la reacción de los consumidores ante los cambios en el precio. Normalmente, la elasticidad es negativa: si el precio de un bien aumenta, es probable que el comprador compre menos, al menos si se trata de un bien normal.

Se dice que una elasticidad mayor que 1 en valor absoluto (menor que -1) está asociada a una reacción elástica al precio, mientras que una elasticidad entre 0 y 1 en valor absoluto (entre -1 y 0) se dice que está asociada a una reacción inelástica al precio.

La teoría económica predice que diferentes factores afectarán la elasticidad precio de la demanda. Por ejemplo, la ausencia o escasez de sustitutos conducirá a una mayor elasticidad en valores absolutos.

Cálculo de elasticidad de muestra: uso de datos de muestra

Calcule la elasticidad a partir de los siguientes datos de muestra:

Pag	Q
1	10
2	13.4
3	15.8
4	21.2
5	26.7
6	40.1

Solución :Para encontrar la elasticidad precio de la demanda a partir de estos datos, necesitamos construir un modelo de regresión log-log, donde la variable independiente que utilizaremos es \(ln(P)\), y la variable dependiente es el logaritmo natural de \(ln(Q)\)

Para calcular los coeficientes de regresión para esta regresión auxiliar, se debe utilizar la siguiente tabla:

	Pag	Z = ln(P)	Q	W = ln(Q)	\(Z \cdot W\)	\(Z^2\)	\(W^2\)
	1	0	10	2.303	0	0	5.302
	2	0.69	13.4	2.595	1.8	0.48	6.735
	3	1.1	15.8	2.76	3.03	1.21	7.618
	4	1.39	21.2	3.054	4.23	1.92	9.327
	5	1.61	26.7	3.285	5.29	2.59	10.789
	6	1.79	40.1	3.691	6.61	3.21	13.626
Sum =	21	6.58	127.2	17.688	20.97	9.41	53.397

Con base en la tabla anterior se calcula lo siguiente:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 6.579}{ 6} = 1.097\]\[\bar W = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 17.688}{ 6} = 2.948\] \[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 9.41 - 6.579^2/6 = 2.195\] \[\large SS_{WW} = \sum_{i=1}^{n} W_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} W_i\right)^2 = 53.397 - 17.688^2/6 = 1.254\] \[\large SS_{ZW} = \sum_{i=1}^{n} Z_i W_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} W_i\right) = 20.965 - 6.579 \times 17.688/6 = 1.57\]

Por lo tanto, en base a los cálculos anteriores, los coeficientes de regresión (la pendiente \(m\) y la intersección con el eje y \(n\)) se obtienen de la siguiente manera:

\[m = \frac{SS_{ZW}}{SS_{ZZ}} = \frac{ 1.57}{ 2.195} = 0.715\]\[n = \bar W - \bar Z \cdot m = 2.948 - 1.097 \times 0.715 = 2.1639\]

Por lo tanto, encontramos que la ecuación de regresión es:

\[W = 2.1639 + 0.715 \text{ Z}\]

Pero como las variables auxiliares son \(Z = \ln(X)\) y \(W = \ln(Y)\), concluimos que la ecuación de regresión log-log es:

\[\ln(Q) = 2.1639 + 0.715 \ln(P)\]

Por tanto, con base en la información proporcionada anteriormente, se obtienen los siguientes diagramas de dispersión y de regresión:

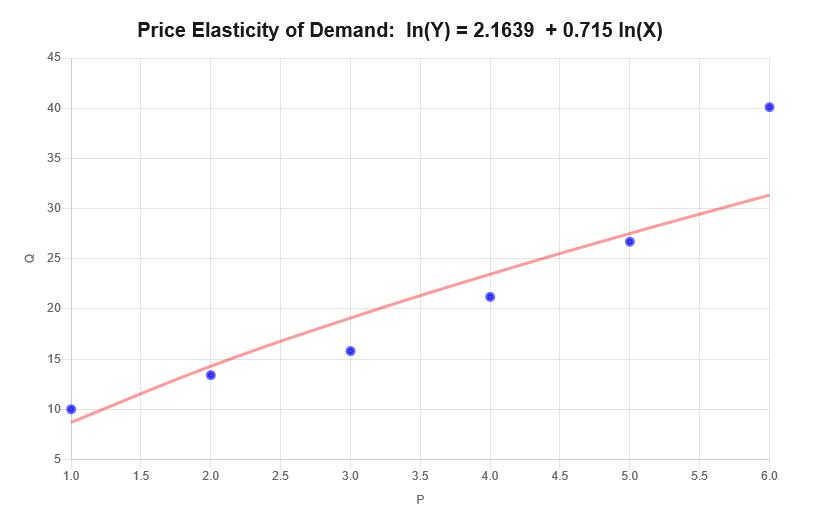
Interpretación

La elasticidad en este caso corresponde al coeficiente de pendiente de los datos proporcionados, lo que significa \(\varepsilon = 0.715 \), lo que puede interpretarse de la siguiente manera:

• Para un aumento del 1% en el precio, hay un aumento promedio del 0,715% en la cantidad demandada.

Más calculadoras interesantes

La estimación de modelos a partir de datos de muestra es una habilidad fundamental necesaria tanto en estadística como en economía. El uso de datos de muestra para Calcular un modelo de regresión Es una de las aplicaciones más comunes del uso de datos de muestra para la construcción de modelos.

Pero a menudo ocurre que un modelo lineal regular no se ajusta lo suficientemente bien a los datos, por lo que necesitamos intentar estructuras funcionales diferentes. Por ejemplo, podríamos estimar una Regresión logarítmica , a regresión logarítmica o un Regresión polinomial , por mencionar solo algunos, que podrían ser más exitosos para explicar la variación en la variable dependiente que la regresión regular.

La opción de Cálculo de la elasticidad a partir de datos de muestra se utiliza principalmente en un contexto exploratorio. La mayoría de las veces, el La elasticidad se calcula directamente a partir de la función de demanda , cuando esté disponible. En otras circunstancias, la elasticidad se estima a partir de un par de puntos de precio-demanda utilizando el fórmula de elasticidad del arco .