Quadratischer gleichungslöser

Dieser Taschenrechner ermöglicht es Ihnen Berechnen Sieger Quadratische Gleisung das Sie zur Verfügung stellen und alle Schritte zeigen.Sie müssen lediglich eine gültige quadratische Gleichung bereitstellen.

Es könnte etwas sein, das bereits vereinfacht und bereit ist, wie x^2 + 3x + 5 = 0 zu lösen.1 zum Beispiel.

Sobald Sie eine gültige quadratische Gleichung bereitstellen, müssen Sie lediglich auf "Berechnen" klicken, und Sie erhalten alle Schritte des Prozesses, um die zu berechnen Wurzeln der Quadratischen Gleisung das ist bereitgestellt.

Normalerweise verwenden Sie die quadratische Formel, um quadratische Gleichungen zu berechnen, aber das ist nicht der einzige Weg, wie wir in den folgenden Abschnitten sehen werden.

Wie berechnet man eine quadratische gleichung?

Es gibt mehrere Strategien zur Lösung quadratischer Gleichungen.Das am häufigsten verwendete ist die Verwendung des Quadratische Formel .Außerdem können Sie durch lösen Quadriert Vervollstangigen , oder Sie können durch lösen Quadratische Faktorierung .

Was sind die schritte zur berechnung der quadratischen gleichungen mithilfe der quadratischen formel?

• Schritt 1: Identifizieren Sie die quadratische Gleichung, die Sie berechnen möchten
• Schritt 2: Stellen Sie sicher, dass die Gleichung vollständig vereinfacht ist, andernfalls fahren Sie mit der Vereinfachung fort, bis Sie eine Gleichung der Form AX² + BX + C = 0 haben
• Schritt 3: Nachdem die Gleichung auf ihre vereinfachte Form reduziert wurde, können Sie die quadratische Formel verwenden: \(x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

Möglicherweise ist die Verwendung der quadratischen Gleichungsformel die praktischste Möglichkeit, die Wurzeln einer quadratischen Gleichung zu finden, aber es gibt andere Gründe, warum Sie andere Methoden würden.

Wie löse ich eine quadratische gleichung, indem ich quadrate vervollständigst?

Die zweithäufigste Art der Lösung einer quadratischen Gleichung ist die Verwendung der Technik von Quadriert Vervollstangigen .Es gibt nicht wirklich eine Formel zum Abschluss von Quadraten (obwohl es technisch gesehen eine auf den Lösungen der quadratischen Gleichung gibt) und eher ein Prozess.

Was sind die schritte zum ausfüllen von quadraten

• Schritt 1: Identifizieren Sie die quadratische Gleichung, die Sie lösen möchten
• Schritt 2: Sie müssen sicherstellen, dass die Gleichung vollständig vereinfacht ist und dass Sie eine Gleichung der Form AX² + BX + C = 0 haben
• Schritt 3: Fügen Sie einen geeigneten Begriff (in diesem Fall (b/(2a))) ² hinzu und subtrahieren Sie sie, um die Begriffe des Quadrats eines Binomials zu erzwingen

Die Idee, das Erscheinungsbild eines Begriffs der Form (x + "etwas) ² zu erzwingen, was das ultimative Ziel des Abschlusses von Quadräten ist.

Warum sollten sie quadratische gleichungen verwenden?

Quadratische Gleichungen erscheinen ständig in den Algebra -Anwendungen, die Wortprobleme sind.Das Lösen von quadratischen Gleichungen ist eine grundlegende Kernfähigkeit, die Sie erwerben müssen.

In Feldern wie Kalkül müssen Sie dann bei Berechnung von Maximierungs- und Minimierungsproblemen eine gute Vertrautheit mit allen Arten von quadratischen Gleichungen haben.

Beispiel: lösen einer quadratischen gleichung

Lösen Sie die folgende quadratische Gleichung mit der Formel \(4x^2 + \frac{4}{3}x + 2 = 0\)

Lösung: Wir müssen die folgende quadratische Gleichung lösen \(\displaystyle 4x^2+\frac{4}{3}x+2=0\).

Für eine quadratische Gleichung der Form \(a x^2 + bx + c = 0\) werden die Wurzeln unter Verwendung der folgenden Formel berechnet:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In diesem Fall haben wir, dass die Gleichung, die wir lösen müssen, \(\displaystyle 4x^2+\frac{4}{3}x+2 = 0\) ist, was impliziert, dass entsprechende Koeffizienten sind:

\[a = 4\] \[b = \frac{4}{3}\] \[c = 2\]

Erstens werden wir die Diskriminanz berechnen, um die Art der Wurzeln zu bewerten.Die Diskriminierung wird berechnet als:

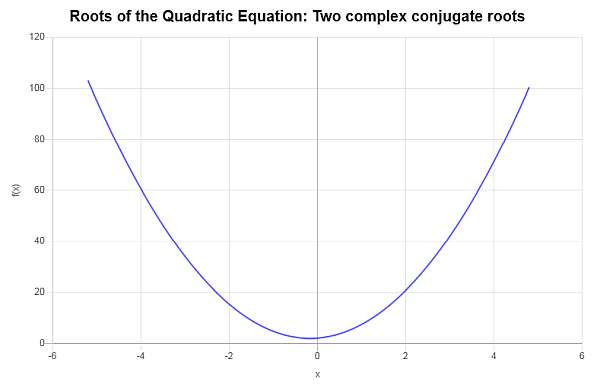
\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{4}{3}\right)^2 - 4 \cdot \left(4\right)\cdot \left(2\right) = -\frac{272}{9}\]

Da wir in diesem Fall die Diskriminanz erhalten, ist \(\Delta = \displaystyle -\frac{272}{9} < 0\), was negativ ist, wir wissen, dass die gegebene Gleichung zwei verschiedene konjugierte Komplexwurzeln hat.

Stecken Sie diese Werte nun in die Formel für die Wurzeln, die wir erhalten:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{\left(\frac{4}{3}\right)^2-4\left(4\right)\left(2\right)}}{2\cdot 4} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{-\frac{272}{9}}}{8}\]

Also finden wir das:

\[\displaystyle x_1 = \frac{-\frac{4}{3} - i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\] \[\displaystyle x_2 = \frac{-\frac{4}{3} + i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\]

Daher hat die gegebene Gleichung \(\displaystyle 4x^2+\frac{4}{3}x+2=0\) zwei verschiedene konjugierte komplexe Wurzeln, die \(x_1 = \displaystyle -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\) und \(x_2 = \displaystyle -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\) sind.

Grafisch:

Beispiel: wurzel einer quadratischen gleichung

Finden Sie die Wurzeln der folgenden quadratischen Gleichung, indem Sie Quadrate vervollständigen \(2x^2 + \frac{1}{3}x + \frac{1}{72} = 0\)

Lösung: In diesem Fall haben wir, dass die Gleichung, die wir lösen müssen, \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72} = 0\) ist, was impliziert, dass entsprechende Koeffizienten sind:

\[a = 2\] \[b = \frac{1}{3}\] \[c = \frac{1}{72}\]

Die Diskriminierung wird berechnet als:

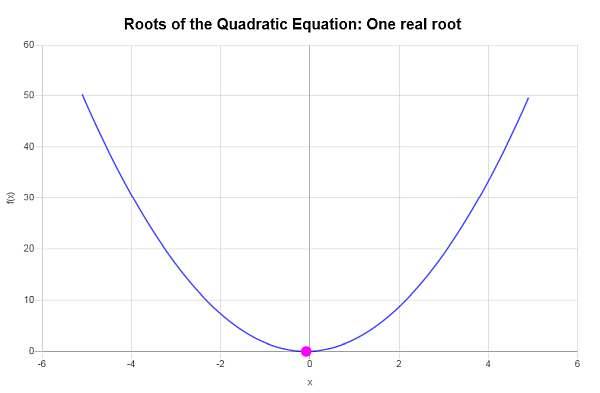
\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{1}{3}\right)^2 - 4 \cdot \left(2\right)\cdot \left(\frac{1}{72}\right) = 0\]

Da wir in diesem Fall die Diskriminanz erhalten, ist \(\Delta = \displaystyle 0 = 0\), was Null ist, wir wissen, dass die Gleichung nur eine echte Wurzel hat.

Stecken Sie diese Werte nun in die Formel für die Wurzeln, die wir erhalten:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{\left(\frac{1}{3}\right)^2-4\left(2\right)\left(\frac{1}{72}\right)}}{2\cdot 2} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{0}}{4}\]

Also finden wir das:

\[x = \displaystyle \frac{-\frac{1}{3}}{4} = \displaystyle -\frac{1}{12}\]

Daher hat die gegebene Gleichung \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72}=0\) nur eine echte Wurzel, nämlich \(x = \displaystyle -\frac{1}{12}\).

Grafisch:

Beispiel: wurzeln der gleichungsberechnung

Lösen Sie Folgendes: \(3x^2 + \frac{2}{3}x - \frac{4}{3} = 0\)

Lösung: In diesem Beispiel ist die Gleichung, die wir lösen müssen, \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3} = 0\), also sind die entsprechenden Koeffizienten:

\[a = 3\] \[b = \frac{2}{3}\] \[c = -\frac{4}{3}\]

In diesem Fall wird die Diskriminierung berechnet als:

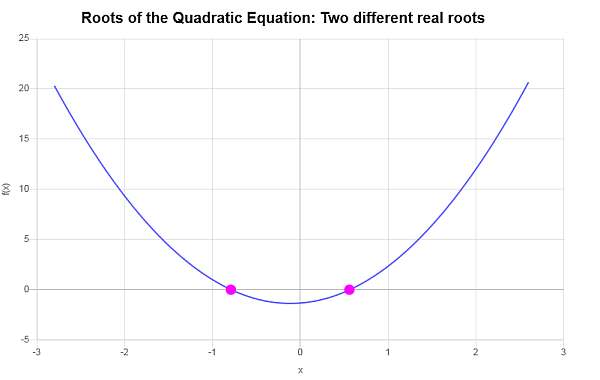
\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{2}{3}\right)^2 - 4 \cdot \left(3\right)\cdot \left(-\frac{4}{3}\right) = \frac{148}{9}\]

Da die Diskriminanz \(\Delta = \displaystyle \frac{148}{9} > 0\) ist, was positiv ist, wissen wir, dass die Gleichung zwei verschiedene reale Wurzeln haben wird.

Stecken Sie diese Werte nun in die Formel für die Wurzeln, die wir erhalten:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\left(\frac{2}{3}\right)^2-4\left(3\right)\left(-\frac{4}{3}\right)}}{2\cdot 3} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\frac{148}{9}}}{6}\]

Also finden wir das:

\[ x_1 = -\frac{\frac{2}{3}}{6}-\frac{1}{6}\sqrt{\frac{148}{9}}=-\frac{1}{9}\sqrt{37}-\frac{1}{9} \] \[x_2 = -\frac{\frac{2}{3}}{6}+\frac{1}{6}\sqrt{\frac{148}{9}}=\frac{1}{9}\sqrt{37}-\frac{1}{9}\]

Daher hat die gegebene Gleichung \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3}=0\) zwei verschiedene reale Wurzeln, nämlich \(x_1 = \displaystyle -\frac{1}{9}\sqrt{37}-\frac{1}{9}\) und \(x_2 = \displaystyle \frac{1}{9}\sqrt{37}-\frac{1}{9}\).

Grafisch:

Andere nützliche quadratische taschenrechner

Wie wir in diesem Tutorial gesehen haben, Quadriert Vervollstangigen spielt eine grundlegende Rolle bei der Berechnung der quadratischen Gleichungen.Sie können dies auch verwenden Diskriminanzrechner Um die Art der Wurzeln (zwei reale Wurzeln, eine reale Wurzel oder zwei komplexe Wurzeln) zu bewerten, ohne die Gleichung zu lösen.

Sie können dies auch verwenden Scheitelpunktrechner um die Koordinaten des Scheitelpunkts einer quadratischen Gleichung zu finden, und Funde sie Die Symmetriseachse Einer Parabel .Sie können dies auch untersuchen Quadratische Faktorierung Werkzeug zur Erforschung einer weiteren Möglichkeit zur Berechnung der quadratischen Gleichungen.