Mehr zu diesem quadratischen graphentgenerator

Mit diesem quadratischen Graphenrechner können Sie den Diagramm für jede von Ihnen bereitgestellte quadratische Funktion erstellen.Es kann jede gültige quadratische Funktion sein, z. B. x^2 - 3x + 1/2, aber Sie können auch eine quadratische Funktion liefern, die nicht vereinfacht wird, wie x^2 - 3x - 4 - 1/2 x^2 -1/5, vorausgesetzt, das ist eine gültige quadratische Funktion.

Sobald Sie einen gültigen quadratischen Ausdruck angeben, können Sie auf die Schaltfläche "Berechnen" klicken und die Grafik der Funktion wird generiert und zeigt Ihnen die Schritte der Berechnung der Scheitelpunkt der Parabel und die Symmetriseachse auch .

Quadratische Funktionen spielen eine vorherrschende Rolle, die grundlegende Algebra ist, da sie häufig im Kontext der Lösung für verwendet werden quadratische Gleisungen und Anwendungsprobleme.Sie sind im Wesentlichen grundlegend Polynom Das hat viele interessante Eigenschaften.

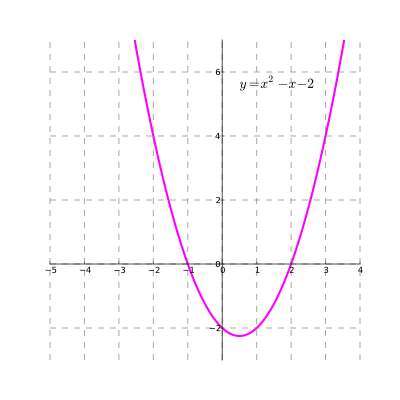
Wie grafi die quadratik?

Eine quadratische Grafik zu machen ist einfach in dem Sinne, dass Sie wissen, dass alle quadratischen Funktionen die Form einer Parabel haben.Trotzdem gibt es unendliche Parabel.Wir müssen ein bisschen mehr wissen, um die genaue Parabola zu identifizieren, die eine bestimmte quadratische Funktion darstellt.

Schritte, um eine quadratische funktionsgrafik zu finden

• Schritt 1: Identifizieren Sie klar die angegebene quadratische Funktion und vereinfachen Sie bei Bedarf bei Bedarf
• Schritt 2: Identifizieren Sie nach der Vereinfachung die Funktion in Form F (x) = AX² + BX + C.Beachten Sie, dass A nicht Null sein kann
• Schritt 3: Wenn a> 0, wissen Sie, dass die Grafik eine Parabola ist, die nach oben geöffnet wird, während bei A <0, Sie wissen, dass die Grafik eine Parabola ist, die sich nach unten öffnet
• Schritt 4: Die Symmetrieachse liegt bei x* = -b/(2a), der Ihnen das 'Zentrum' der Parabel sagt
• Schritt 5: Hinweis x*= -b/(2a) ist der X -Koordinate des Scheitelpunkts der Parabola und y*= f (x*) = a (x*) ² + b (x*) + C istder Y-Koordinate des Scheitelpunkts

Das sollte ausreichen, um eine klare Vorstellung über das entsprechende quadratische Graphen zu haben.Ein weiterer Schritt wäre, einige Punkte in der Grafik zu zeichnen, indem sie unterschiedliche Punkte in der X-Achse auswählen und ihr entsprechendes Bild durch die Funktion finden. Grafik der Funktion .

Die quadratische formel

Ist der Quadratische Formel Bezogen auf die Grafik einer quadratischen Funktion?Sie wetten!Geometrisch gesehen die beim Lösen der quadratischen Gleichung

\[a x^2 + bx + c = 0 \]

Sie erhalten die Wurzeln der quadratischen Gleichung, und wenn die Wurzeln real sind, repräsentieren sie die Punkte, an denen die Parabel die X-Achse überschreitet.

Ein Sonderfall tritt auf, wenn die Wurzeln komplex sind. In diesem Fall wird die Parabola die X-Achse nicht überschreiten.

Arten von quadratischen graphen

Wie bereits erwähnt, werden alle univariaten quadratischen Funktionen durch Parabel dargestellt, aber je nachdem, ob a> 0 oder a <0, werden die Parabolas jeweils geöffnet.

Eine weitere Unterscheidung der Arten von Parabolas könnte für diejenigen sein, die "zentriert" sind (dies ist, die, die Scheitel ist ein der Ursprung) und diejenigen, die nicht sind.

Beispiel: quadratische grafik

Konstruieren Sie das Diagramm von: \(f(x) = \frac{1}{3}x^2 +2x - 3\)

Lösung:

Wir müssen die bereitgestellte quadratische Funktion \(f(x) = \displaystyle \frac{1}{3}x^2+2x-3\) grafisch darstellen.Außerdem werden die Koordinaten des Scheitelpunkts berechnet.

Für eine quadratische Funktion des Formulars \(f(x) = a x^2 + bx + c\) wird die X-Koordinate des Scheitelpunkts unter Verwendung der folgenden Formel berechnet:

\[x_V = \displaystyle -\frac{b}{2a}\]

In diesem Fall haben wir die Funktion, für die wir den Scheitelpunkt finden müssen, für \(f(x) = \displaystyle \frac{1}{3}x^2+2x-3\), was impliziert, dass entsprechende Koeffizienten sind:

\[a = \frac{1}{3}\] \[b = 2\] \[c = -3\]

Stecken Sie die bekannten Werte von << xyz >> und << xyz >> in die Formel für die X-Koordinate des Scheitelpunkts, wir erhalten:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{2}{2 \cdot \frac{1}{3}} = -3\]

Jetzt müssen wir den Wert von \(x_V = \displaystyle -3\) in die quadratische Funktion anschließen, damit wir:

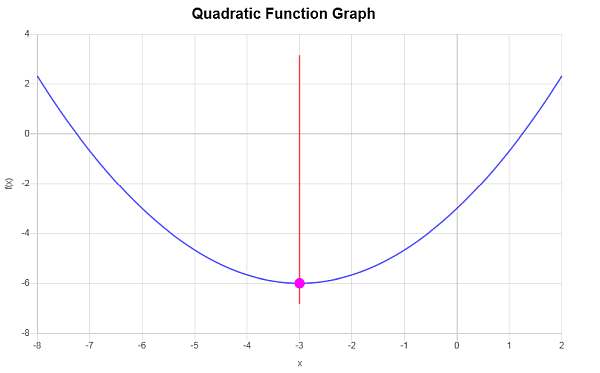
\[y_V = f(x_V)\] \[ = \frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=\frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=9\cdot\frac{1}{3}-6-3=3-6-3=-6\]

Daher ist der X-Koordinat des Scheitelpunkts \(x_V = \displaystyle -3\) und der y-Koordinat des Scheitelpunkts ist \(y_V = \displaystyle -6\).Dies zeigt an, dass der Punkt, der den Scheitelpunkt darstellt, \( \displaystyle \left(-3, -6\right)\) ist.

Das Folgende wird grafisch erhalten:

Beispiel: quadratische grafik

Graph: \(f(x) = \frac{4}{3}x^2 +3x - 2\), welche Art von quadratischer Grafik ist das?

Lösung: In diesem Fall haben wir die Funktion, für die wir den Scheitelpunkt finden müssen, für \(f(x) = \displaystyle \frac{4}{3}x^2+3x-2\), was impliziert, dass entsprechende Koeffizienten sind:

\[a = \frac{4}{3}\] \[b = 3\] \[c = -2\]

Stecken Sie die bekannten Werte von << xyz >> und << xyz >> in die Formel für die X-Koordinate des Scheitelpunkts, wir erhalten:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot \frac{4}{3}} = -\frac{9}{8}\]

Jetzt müssen wir den Wert von \(x_V = \displaystyle -\frac{9}{8}\) in die quadratische Funktion anschließen, damit wir:

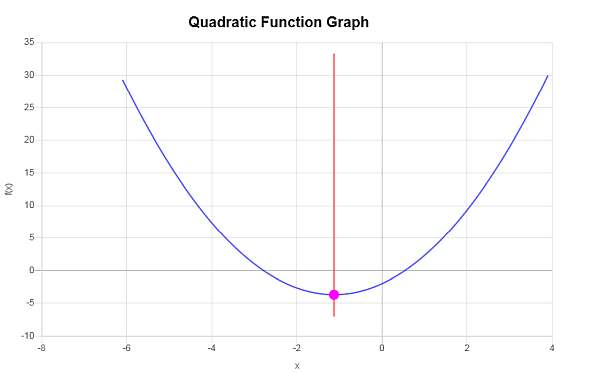
\[y_V = f(x_V)\] \[ = \frac{4}{3}\cdot \left(-\frac{9}{8}\right)^2+3\cdot \left(-\frac{9}{8}\right)-2=\frac{4}{3}\cdot\frac{81}{64}+3\cdot \left(-\frac{9}{8}\right)-2=\frac{27}{16}-\frac{27}{8}-2=-\frac{59}{16}\]

Daher ist der X-Koordinat des Scheitelpunkts \(x_V = \displaystyle -\frac{9}{8}\) und der y-Koordinat des Scheitelpunkts ist \(y_V = \displaystyle -\frac{59}{16}\).Dies zeigt an, dass der Punkt, der den Scheitelpunkt darstellt, \( \displaystyle \left(-\frac{9}{8}, -\frac{59}{16}\right)\) ist.

Das Folgende wird grafisch erhalten:

Mehr quadratische taschenrechner

Die meisten Anwendungen in Basisalgebra basieren auf der Lösung einer Art von Quadratische Gleisung Es hat also einen starken pädagogischen Zweck, darüber zu lernen.

Das Quadratische Formel ist eines der berüchtigtsten lehrbaren Objekte in Mathematik.Es ist nicht so, dass kubische oder quartische Gleichungen nicht existieren, sondern das ist das quadratische Gleisungen sind die, die wir leicht erklären können.