Funções racionais

Esta calculadora de função racional permitirá analisar os pontos mais relevantes de uma função racional que você fornece, com todos os passos mostrados. Normalmente, para a maioria das funções racionais você pode encontrar interceptos, assíntotas verticais e seu gráfico. Algumas funções racionais específicas também terão assíntotas horizontais.

O tipo de função que você pode fornecer é como 'f(x)=1/x - x', ou algo envolvendo polinômios de grau superior como 'f(x) = (x^3-1)/(x^2+x )'

Depois que uma função racional válida for fornecida, você pode clicar no botão calcular e obterá todas as etapas mostradas para você.

Um dos principais atributos de uma função racional é que você pode reduzir principalmente o cálculo ao problema de resolvendo equações polinomiais , que é um dos tipos "mais simples" de equações que você pode resolver .

O que é uma função racional

Uma função racional é uma função que envolve o quociente de dois polinômios \(P(x)\) e \(Q(x)\), onde o divisor \(Q(x)\) não é igual ao polinômio zero. Então, a fórmula da função racional é

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \]

Por exemplo, a função

\[\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \]

é uma função racional, porque é precisamente o quociente de dois polinômios. Mas por exemplo

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{\sin x} \]

não é racional porque o divisor não é um polinômio. Observe que quando dizemos que o divisor \(Q(x)\) não é igual ao polinômio zero, NÃO estamos dizendo que \(Q(x)\) não pode ter zeros. Por exemplo, neste caso de \(\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \), o divisor é \(Q(x) = x + 1\), que tem um zero, em \(x = -1\).

O que não queremos é algo como

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{0} \]

porque embora neste caso \(Q(x) = 0\) seja tecnicamente um polinômio, é o polinômio zero (que é zero em todos os lugares).

Etapas para calcular uma função rational

• Passo 1: Primeiro, certifique-se de ter uma função racional, para a qual você possa identificar o numerador P(x) e o denominador Q(x)
• Passo 2: Se você não encontrar estritamente a estrutura descrita acima, pare. Talvez seja necessário agrupar os termos por meio de reduções algébricas .
• Etapa 3: Você precisa encontrar os zeros reais de P(x) e Q(x), se houver. As conclusões encontradas estarão intimamente relacionadas aos zeros de P(x) e Q(x)
• Passo 4: Para encontrar a interceptação y, você avalia a função em zero, calculando f(0). A interceptação y será bem definida se x = 0 não for zero de Q(x)
• Passo 5: Para encontrar as interceptações x, você obtém os zeros de P(x) que não são zeros de Q(x)
• Passo 6: Para encontrar assíntotas verticais, você precisa encontrar os zeros de Q(x) que não sejam zeros de P(x)
• Etapa 7: Para encontrar assíntotas horizontais, você precisa que o grau de Q(x) seja maior ou igual ao grau P(x)

Observe que, como esperado, a análise de uma função racional depende de Encontrando zeros de um polinômio e, em seguida, juntando todas as conclusões. .

Observe que o domínio de uma função racional é toda a reta real, exceto os zeros do divisor Q(x). Se houver um zero de Q(x) que também seja um zero de P(x), então a descontinuidade pode ser reparada. O contradomínio de uma função racional dependerá dos graus de P(x) e Q(x).

Por que usar funções racionais

Funções racionais são usadas porque são extensões naturais de polinômios. Pode-se vê-los como o próximo passo na complexidade de uma função. Como sabemos, expressões polinomiais estão entre as funções mais simples que podemos encontrar, mas também estão entre as mais úteis.

Equações racionais normalmente aparecerão em problemas de mistura mais avançados e, ainda assim, são surpreendentemente simples de manusear, desde que os polinômios envolvidos sejam bastante simples. Nós sabemos como resolver equações quadráticas , mas para polinômios de grau 3 e superiores as coisas podem ser mais complicadas.

As funções polinomiais também são funções racionais

Sim, se P(x) é um polinômio, então P(x) também é racional, porque podemos escrever:

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{1} \]

e Q(x) = 1 é um polinômio real. O contrário não é verdade: uma função racional não é necessariamente um polinômio. Por que é que? Porque naturalmente, a menos que Q(x) = 1, sempre que você tiver \(\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \), você não terá que todos os termos serão termos livres conforme exigido pela definição de um polinômio.

Mais formalmente, usando Teorema Do Resto , Nós temos

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} = d(x) + \frac{r(x)}{Q(x)}\]

onde \(d(x)\) é um polinômio, mas \frac{r(x)}{Q(x)} não é, porque o grau de r(x) é menor que o grau de Q(x).

Exemplo: trabalhando com funções racionais

Encontre as interceptações e assíntotas e o gráfico de: \(f(x) = \frac{x^2-1}{x+1}\)

Solução:

Recebemos a seguinte função:

\[f\left(x\right)=\frac{x^2-1}{x+1}\]

Precisamos encontrar as interceptações e assíntotas, se houver. Em seguida, será apresentado o gráfico da função.

Vamos encontrar os zeros da função dada. Precisamos resolver a seguinte equação racional:

\[\frac{x^2-1}{x+1}=0\]

Observe que para \(x \ne -1\) podemos simplificar como:

\[\frac{x^2-1}{x+1} = 0 \Rightarrow \frac{(x-1)(x+1)}{x+1} = 0 \Rightarrow x-1 = 0\]

Equação do numerador auxiliar

Agora igualamos o numerador a zero e encontramos as soluções. Então, aquelas raízes que não tornam o denominador igual a zero serão soluções da equação racional.

O seguinte precisa ser resolvido para encontrar as raízes do numerador: \(x^2-1=0\)

Para uma equação quadrática da forma \(a x^2 + bx + c = 0\), as raízes são calculadas usando a seguinte fórmula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

Neste caso, temos que a equação que precisamos resolver é \(\displaystyle x^2-1 = 0\), o que implica que os coeficientes correspondentes são:

\[a = 1\] \[b = 0\] \[c = -1\]

Primeiro, calcularemos o discriminante para avaliar a natureza das raízes. A discriminação é calculada como:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-1\right) = 4\]

Como neste caso obtemos o discriminante \(\Delta = \displaystyle 4 > 0\), que é positivo, sabemos que a equação tem duas raízes reais diferentes.

Agora, inserindo esses valores na fórmula das raízes, obtemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-1\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{4}}{2}\]

então, descobrimos que:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{4}=\frac{0}{2}-1=-1 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{4}=\frac{0}{2}+1=1\]

Equação do denominador auxiliar

Precisamos encontrar as raízes do denominador: \(x+1=0\)

Portanto, a resolução de \(x\) para determinada equação linear leva a \(x=-1\).

Numerador e denominador zeros

Com base na análise mostrada acima, os zeros reais do numerador da função racional dada são \( x_{ 1} = -1\) e \( x_{ 2} = 1\).

Também se verifica que o denominador possui um zero real, que é \( x_{ 1} = -1\).

Encontrando interceptações x

Com base nos zeros do numerador que não são zeros do denominador, descobrimos que existe uma interceptação x, que é \(\left(1, 0\right)\).

Encontrando interceptações y

Ao avaliar a função fornecida em \(x = 0\), descobrimos que:

\[ f(0) = \frac{0^2-1}{0+1} = -1\]

então a interceptação y é \( \left(0, -1\right)\).

Assíntotas verticais

Após análise dos zeros, conclui-se que a função não possui assíntotas verticais.

Assíntotas horizontais

Observe que o grau do numerador é \(2\) e o grau do denominador é \(1\), e então, como o grau do polinômio no numerador excede aquele no denominador, concluímos que não há horizontal assíntota.

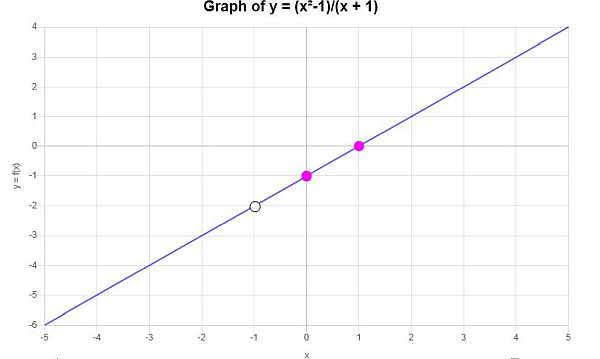
Obtém-se o seguinte gráfico:

Exemplo: assíntotas horizontais

Esta função racional tem uma assíntota horizontal: \(f(x) = \frac{x^2-1}{x^2+1}\)?

Solução: É claro que neste caso a função consiste no quociente de dois polinômios, e ambos têm grau igual a 2. Ou seja, têm o mesmo grau e portanto, existe uma assíntota horizontal.

Podemos ver isso usando limites também:

\[\lim_{x\to +\infty} f(x) = \lim_{x\to +\infty}\frac{x^2-1}{x^2+1} = \lim_{x\to +\infty}\frac{1-\frac{1}{x^2}}{1+\frac{1}{x^2}} = 1\]

o que implica que a assíntota horizontal é \(y = 1\). Isso conclui o cálculo.

Calculadoras de funções úteis

Funções são objetos matemáticos fundamentais, que encapsulam a relação entre diferentes variáveis. Usando um calculadora de funções pode ajudá-lo a lidar sistematicamente com funções que podem ser muito complicadas para serem manuseadas manualmente.

Representando graficamente funções racionais é um dos exemplos de brinquedo mais comuns que os alunos aprendem em Álgebra e Cálculo e, embora talvez as funções racionais não apareçam per se com tanta frequência nas aplicações, as habilidades analíticas necessárias para lidar com elas podem ser inestimáveis

O mesmo vale para Resolvendo Equações Racionais , onde os princípios de manipular expressões algébricas e reduzi-las aos seus termos inferiores serão extremamente poderosos para a obtenção de competências mais avançadas.

Agora, se estamos falando de função, não podemos esquecer o cálculo da derivada de uma função , integração e outras técnicas infinitesimais mais avançadas.