Calculadora de equação racional
Instruções: Use esta calculadora de equações racionais para calcular a solução para qualquer equação racional fornecida, mostrando todas as etapas. Por favor, digite a equação que deseja resolver na caixa abaixo.
Resolvendo equações racionais
Usando esta calculadora com etapas, você poderá trabalhar facilmente na resolução de equações racionais. A maneira como isso funciona é simplesmente fornecer uma equação racional na caixa acima. Esta equação pode ser tão simples quanto 'x ^ (1/2) = x ^ (1/4)' ou mais complicada do que isso, se necessário.
Então, quando terminar de digitar ou colar a equação desejada, você poderá clicar no botão "Resolver", que irá resolva a equação e mostrará todas as etapas do caminho.
Equações racionais, como outros tipos de equações não lineares, serão em geral difíceis de resolver, se é que você consegue resolvê-las. Geralmente, apenas alguns Equações Racionais , com certas estruturas específicas poderão ser resolvidas explicitamente usando alguns truques padrão, como o uso de substituições.

O que é uma equação racional
Uma equação racional é um tipo de equação encontrada na álgebra em que em algum ponto da equação você vê um quociente de dois polinômios. Por exemplo
\[\displaystyle \frac{x}{x+1} + 4 = 1\]é uma equação racional, por causa do termo \(\frac{x}{x+1} \). Tecnicamente, todas as equações polinomiais também são equações racionais, porque um polinômio sempre pode ser considerado dividido por 1, e 1 é um polinômio de ordem 0 (uma constante).
O acima é uma maneira elegante de expressar \(P(x) = \frac{P(x)}{1}\).
Fórmula de equação racional
Não existe uma fórmula específica para uma equação racional, mas você deverá ser capaz de identificá-las sempre que o quociente de dois denominadores aparecer em uma equação. Em termos de fórmula, você está tentando identificar algo como:
\[\displaystyle \frac{P(x)}{Q(x)} \]em algum lugar da equação, para classificá-la como uma equação racional.
Como resolver equações racionais
- Passo 1: Certifique-se primeiro de que você está realmente lidando com uma equação racional. Um tipo diferente de equação muito provavelmente exigirá uma abordagem diferente
- Passo 2: Examine a estrutura e tente ver se uma substituição transforma rapidamente a equação em uma equação polinomial
- Estágio 3: Se uma substituição rápida não for possível, você precisará percorrer o caminho mais longo: encontre denominadores comuns em ambos os lados da equação e multiplique esses denominadores. Isso levará diretamente a uma equação polinomial
Por exemplo, se você precisar resolver esta equação racional \(\frac{1}{x} + \frac{1}{x^2} = 2\), você poderia seguir o caminho mais longo para encontrar o denominador comum, que neste caso seria \(x^2\) e você chegaria a uma equação polinomial.
Mas então, você também poderia fazer a substituição \(u = \frac{1}{x}\), então a equação se transforma na equação auxiliar \(u + u^2 = 2\), que pode ser resolvida imediatamente usando o Fórmula da equação quadrática .
Relação com expressões racionais
Expressões racionais e o simplificação da expressão racional é uma tarefa crucial na hora de resolver equações envolvendo expressões racionais.
Mas, ao mesmo tempo, antes de simplificar e operar cegamente a equação em questão, você desejará avaliar se há ou não uma substituição que reduzirá as coisas a uma equação auxiliar muito simples.

Como usar esta calculadora de equações racionais com etapas
A vantagem da nossa calculadora é que ela fará o cálculo mostrando os passos, o que certamente pode ser útil. O principal é que nem todas as equações racionais terão uma solução que possamos encontrar usando métodos elementares.
Resolvendo equações às vezes é preciso um pouco de astúcia, mas com nossa calculadora você eliminará as suposições.

Exemplo: uma equação racional simples
Resolva a seguinte equação: \(\frac{1}{x} + \frac{1}{x^2} = 2\)
Solução: Temos a seguinte equação
\[\frac{1}{x}+\frac{1}{x^2}=2\]Usamos a substituição: \(u = \frac{1}{x}\) então a equação se torna:
\[u + u^2 = 2\]Esta equação quadrática pode ser colocada como \(u^2 + u - 2 = (u-1)(u+2) = 0\)
o que leva diretamente às soluções \(u = 1, u = -2\). Mas como sabemos que \(u = \frac{1}{x}\), encontramos a seguinte solução para a equação original:
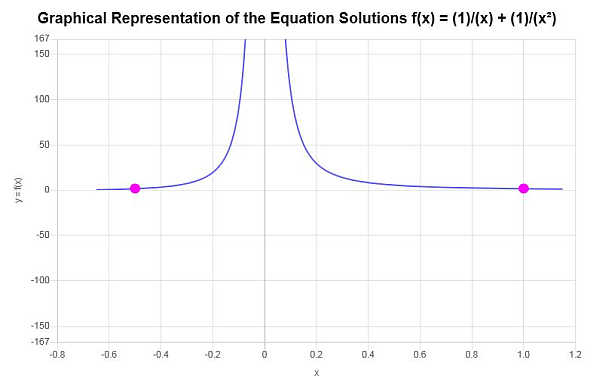
\[x_1 = -\frac{1}{2} \] \[x_2 = 1 \]Portanto, resolver \(x\) para a equação dada leva às soluções \(x=-\frac{1}{2},\,\,x=1\).
Graficamente
A seguir está a representação gráfica das soluções obtidas:
Mais calculadoras de equações
Maioria Calculadoras de equações explorarão estruturas específicas para tentar encontrar uma solução exacta, mas os esforços nem sempre serão bem sucedidos.
Mas, em última análise, não há muito que possa ser feito em geral. A única coisa que podemos fazer é Resolver equações lineares e resolver equações polinomiais (até certo ponto, apenas equações quadráticas são realmente simples de resolver).
Então, qualquer estratégia para resolver uma equação tem a ver com transformá-la de alguma forma usando alguns redução algébrica nos poucos tipos de equações que realmente sabemos como resolver. E principalmente, tudo o que podemos fazer é tentar algumas substituições de sorte, se você tiver sorte.



