Uma calculadora de função

Esta calculadora permitirá que você calcule, simplifique e represente graficamente qualquer função válida que você fornecer, mostrando todas as etapas de simplificação. Você precisa fornecer uma função válida para a calculadora. Pode ser algo já simplificado como f(x) = 2x + 3, pode ser algo mais complexo que requer simplificação, como f(x) = (1/3+1/4)x + x^2 - sin( 1/5+1/6) + 3/4'.

Quando uma função válida é fornecida, basta clicar no botão "Calcular" e o processo de simplificação e gráfico da função será mostrado a você.

As funções são os objetos mais importantes em Álgebra e Cálculo, e ser capaz de calcular e simplificar expressões pode fazer toda a diferença.

Como calcular a função?

A ideia de calcular uma função é simplesmente baseada na definição de uma função, onde para um dado valor \(x\) é atribuído uma 'imagem' que é chamada \(f(x)\).

No gráfico abaixo, você pode ver como um valor "x" no eixo x é atribuído a um ponto "f(x)" no eixo y:

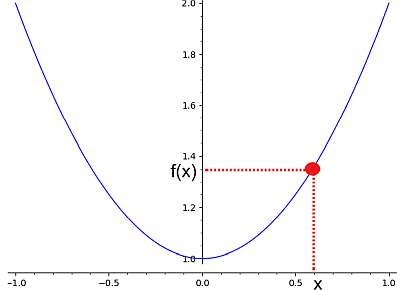
Assim, a ideia de um cálculo de função é obter um valor "x" e poder calcular o valor de "f(x)". Agora, às vezes isso é possível para alguns valores de x, às vezes para todos os valores de x na linha real. O conjunto de valores x onde f(x) pode ser calculado é chamado de domínio de uma função.

Quais são os passos para calcular uma função?

• Passo 1: Identifique a expressão que determina a função
• Etapa 2: simplifique a função o máximo que puder, mas esteja ciente das possíveis divisões por zero
• Etapa 3: observe onde a função pode e não pode ser calculada

Então, conforme você se move junto com isso processo de simplificação , você terá anotado todos os valores em que a função não pode ser avaliada (se houver). Dessa forma, você encontrou indiretamente o domínio da função.

Por exemplo, se você tiver uma função como f(x) = 2x + 1, independentemente do ponto escolhido para x, a expressão '2x + 1' sempre poderá ser calculada. Mas, em vez disso, se você tiver a função f(x) = 1/x, se escolher x = 0, não poderá calcular a função em x = 0, porque isso se tornaria 1/0 e uma divisão por zero é indefinido.

Como simplificar funções?

O processo de simplificação da função é como qualquer simplificação de expressões : você usa os critérios definidos pelo regra PEMDAS para conduzir qualquer simplificação potencial.

Mas há algumas ressalvas ao usar o PEMDAS: você deve evitar divisões inadvertidas por zero ou tirar raízes quadradas de números negativos. Por exemplo, considere a função

\[ f(x) = \displaystyle\frac{2x}{x}\]

Você poderia pensar, bem, vou cancelar x, e então recebo:

\[\displaystyle f(x) = \displaystyle \frac{2\cancel{x}}{\cancel{x}} = 2\]

Mas ao fazer isso você estaria cometendo um erro, porque tal cancelamento de x não pode acontecer quando x = 0. O que você poderia fazer é escrever explicitamente

\[\displaystyle f(x) = \displaystyle \frac{2\cancel{x}}{\cancel{x}} = 2\]

para \(x \ne 0\) e indefinido para \(x = 0\).

Quais são os passos para simplificar?

• Etapa 1: Identifique a função fornecida e certifique-se de que seja uma expressão simbolicamente válida
• Passo 2: Simplifique os termos o máximo possível usando a regra PEMDAS, tomando cuidado para não obter divisões por zero ou raízes quadradas negativas
• Etapa 3: observe os pontos em que a função não pode ser avaliada. O domínio da função será o complemento desses pontos na reta real

muitas vezes, é muito fácil identificar pontos onde pode haver um problema na avaliação da função, por simples inspeção da estrutura da função.

Você pode calcular uma função a partir de pontos?

Depende. O processo de encontrar uma função a partir de pontos dados é chamado interpolação . Agora, para um determinado conjunto de pontos, haverá mais de uma função que passa por esses pontos, então, de certa forma, dar apenas pontos não necessariamente determinará UMA função.

Agora, adicionar certas restrições pode tornar a determinação única. Por exemplo, para dois pontos dados, existe apenas um Função linear (linear afim, para ser mais preciso) que passa por eles. Ou dados quaisquer três pontos, há apenas um função quadrática que passa por eles.

Exemplo: cálculo de função

Calculando e fazendo o gráfico da função: \(f(x) = \frac{1}{3}x + \frac{5}{4}x^2 - \frac{5}{6}\)

Solução: A seguinte função foi fornecida: \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}x^2-\frac{5}{6}\), para a qual precisamos simplificar e construir seu gráfico.

Passo 0: Nesse caso, primeiro precisamos simplificar a função dada \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}x^2-\frac{5}{6} \) e, para isso, notamos que:

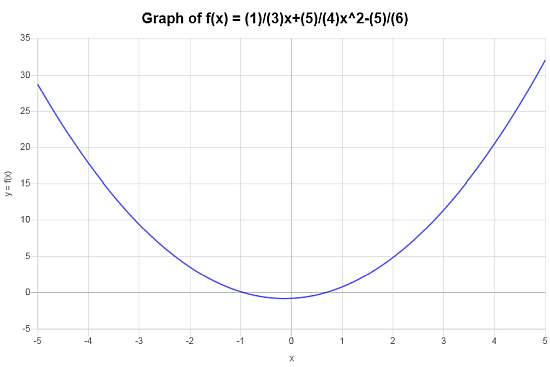
O seguinte gráfico é obtido para \(\displaystyle f(x)=\frac{5}{4}x^2+\frac{1}{3}x-\frac{5}{6}\) no intervalo \([-5, 5]\):

Exemplo: exemplo de calculadora de função

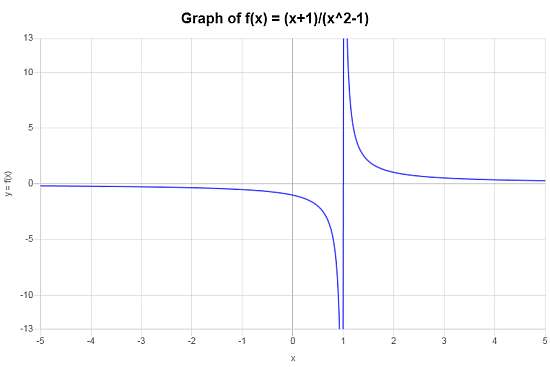
Calcule o domínio da seguinte função: \(f(x) = \displaystyle \frac{x+1}{x^2-1}\)

Solução: A função fornecida \(\displaystyle f(x)=\frac{x+1}{x^2-1}\) pode ser simplificada da seguinte forma:

\[ f(x) = \displaystyle \frac{x+1}{x^2-1} = \displaystyle \frac{x+1}{(x-1)(x+1)} = \displaystyle \frac{1}{x-1} \]

para quando \(x \ne 1\). Portanto, o domínio da função é \((-\infty, 1) \cup (1,\infty)\). O seguinte gráfico é obtido para a função no intervalo \([-5, 5]\):

Exemplo: outro exemplo de calculadora de função

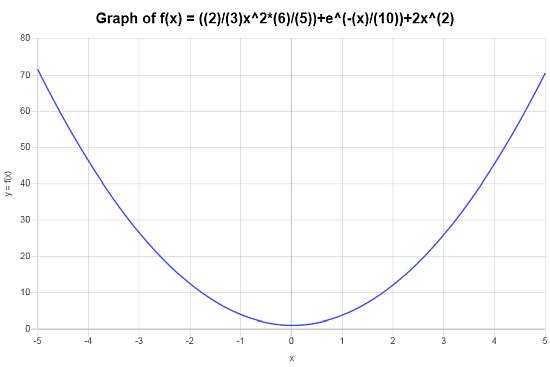
Simplifique e represente graficamente \( f(x) = \left(\frac{2}{3}x^2 \times \frac{6}{5} \right)+ e^{-x/10} + 2x^2 \).

Solução: Dispomos de: \(\displaystyle f(x)=\frac{2}{3}x^2\cdot \frac{6}{5}+e^{\left(-1\right)x/10}+2x^2\). Agora, para simplificar a função dada \(\displaystyle f(x)=\frac{2}{3}x^2\cdot \frac{6}{5}+e^{\left(-1\right)x/10}+2x^2 \), fazemos:

Portanto, o seguinte gráfico é obtido para \(\displaystyle f(x)=\frac{14}{5}x^2+e^{\left(-1/10\right)x}\) no intervalo \([-5, 5]\):

Outras calculadoras de funções

A ideia de função é central para Álgebra e Cálculo. Há muitas coisas que você pode fazer com funções. Uma das principais habilidades que você pode desenvolver é se sentir confortável simplificando expressões , para reduzir a função dada em uma mais simples.

Apenas certifique-se de não obter um gatilho feliz e acabar cancelando zeros e tirando raízes quadradas de números negativos.

Além disso, você pode querer apenas gráfico de uma função , para ter uma ideia melhor de como é a função e quais são suas principais propriedades.