Calculadora derivada

Esta calculadora de derivadas o guiará por todas as etapas e regras usadas para encontrar a derivada de uma determinada função. Você tem que digitar uma função como 3x + sin(x^2), ou você pode prefaciá-la com toda a definição da função, como f(x) = 3x^ 2 + 2tan(x^3).

Observe que isso pode ser chamado de calculadora de primeira derivada, da mesma forma que uma calculadora de derivada. Primeira derivada e derivada representam a mesma coisa, e a "primeira" parte geralmente é descartada.

A função fornecida pode vir totalmente simplificada ou não, não importa, pois a calculadora primeiro simplificará a função se necessário antes de calcular sua derivada.

uma vez por função válida foi fornecido, basta clicar em "Calcular", aguardar alguns segundos, e todas as etapas do cálculo serão apresentadas a você.

A diferenciação é a principal ferramenta usada no Cálculo (juntamente com a integração) e é uma operação crucial que é amplamente usada em matemática mais avançada. Algumas aplicações muito comuns incluem cálculo da linha tangente , máximos e mínimos e muito mais.

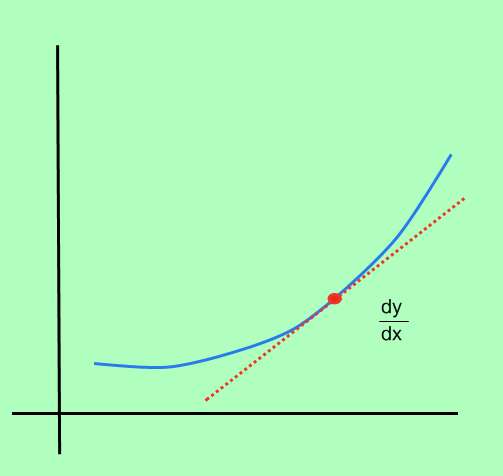
Como calcular a derivada de uma função?

O processo de calcular a derivada de uma função é chamado diferenciação , e consiste em determinar a taxa de variação instantânea do ponto, em cada ponto do domínio da função.

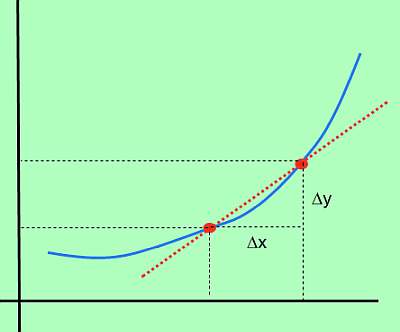
Qual é a taxa instantânea de variação de uma função? Bem, vamos começar com a definição de taxa de variação : Considere uma função \(f\) e suponha que temos dois pontos, \(x_0\) e \(x_1\). No ponto \(x_0\), a função é \(f(x_0)\), e no ponto \(x_1\), a função assume o valor \(f(x_1)\)

Então, a mudança em f é definida como \(\Delta y = f(x_1) - f(x_0)\) (que também é chamada de mudança em y). Além disso, a alteração em x é definida como \(\Delta x = x_1 - x_0)\). Em palavras simples, \(\Delta x\) é a mudança em x, enquanto \(\Delta y\) é a mudança no valor da função devido à mudança em x.

Graficamente:

Fórmula derivada

Assim, se \(\Delta x\) representa a variação de x, e\(\Delta y\) representa a variação do valor da função, devido à variação de x, o correspondente taxa de variação é:

\[\text{Rate of Change} = \displaystyle \frac{\Delta y}{\Delta x} \]

Então, qual seria a taxa instantânea de variação? Isso corresponderia a analisar o que aconteceria se \(\Delta x\) se tornasse muito pequeno. Seria de se esperar que \(\Delta y\) também se tornasse pequeno, mas isso aconteceria com a taxa entre \(\Delta y\) e \(\Delta x\)?

Assim, neste contexto, a taxa instantânea de variação é definida como

\[\text{Instant Rate of Change} = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} \]

Portanto, em termos leigos, definimos \(x_0\) como fixo e calculamos a taxa de variação para valores de \(x_1\) que estão cada vez mais próximos de \(x_0\). Usando essa ideia de taxa de variação instantânea, podemos fornecer a seguinte fórmula para a derivada em um ponto \(x_0\).

\[f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \]

Se o limite acima existir, dizemos que a função f é diferenciável em \(x_0\). Além disso, diremos que uma função é diferenciável em um conjunto A, se a função for diferenciável em todos os pontos do conjunto.

Etapas para usar a fórmula derivada

• Passo 1: Identifique claramente a função f que você deseja diferenciar
• Passo 2: Certifique-se de simplificar f o máximo possível, caso contrário, encontrar o limite necessário pode ser desnecessariamente mais difícil
• Estágio 3: Decida se você trabalhará com um ponto genérico x0 ou se está dando um ponto numérico específico para x0
• Passo 4: Com base na definição da função, use a fórmula \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \). Isto é, coloque os valores de x0 e x1 em f, e veja como fica a fórmula algebricamente
• Passo 5: Simplifique o máximo que puder ANTES de tomar o limite
• Passo 6: Às vezes é mais fácil definir x1 = x0 + h e, em seguida, calcular o limite conforme h converge para 0

Observe que a Etapa 6 é aquela que algumas pessoas gostam como padrão. De fato, a fórmula derivada alternativa que pode parecer mais fácil para fins de simplificação é:

\[f'(x_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \]

que é a fórmula que você pode encontrar em seu livro, em vez da outra.

Regras de derivadas

Pareceria muito trabalhoso calcular a derivada usando a fórmula. E, de fato, poderia ser um processo trabalhoso se decidíssemos resolver todos os processos de diferenciação usando a fórmula da derivada.

Felizmente, existem várias funções (nomeadamente polinômios , funções trigonométricas ) para os quais sabemos com precisão quais são suas derivadas.

Ainda por cima temos regras de diferenciação que nos permitem encontrar a derivada de uma função que é um Função composta e/ou uma combinação de funções elementares (para as quais conhecemos sua derivada), em termos de derivadas elementares.

Quais são as etapas para calcular a derivada?

• Passo 1: Identifique a função f que você deseja diferenciar. Simplifique o máximo que puder ANTES de calcular sua derivada
• Passo 2: Determine se você é obrigado a usar a fórmula derivada ou não
• Estágio 3: Se você deve usar a fórmula derivada, use \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \), ou você pode usar \(f'(x_0) = \displaystyle \lim_{h \to 0}\frac{f(x_0+h) - f(x_0)}{h} \) se parecer mais fácil de abordar
• Passo 4: Se você não for obrigado a usar a fórmula derivada, você pode usar as principais regras de diferenciação: Linearidade, Regra Do Produto , Regra Do Quociente e Regra Da Cadeia , que o ajudará a reduzir o cálculo da derivada para usar derivadas básicas conhecidas

Muitas vezes, a função que você está tentando encontre a derivada for não é uma função simples, mas é uma combinação básica de várias funções simples. Por exemplo, a função

\[f(x) = x + \cos(x) + \sin(x)\]

não é uma função elementar em si, mas é Função composta de três funções elementares, \(x\), \(\sin x\) e \(\cos x\).

Aplicações de derivados

Alguém poderia pensar "bem, derivadas envolvem limites e isso é super teórico, então não deve ter muitas aplicações", mas você estaria completamente errado. A mágica das derivadas é que elas tratam essencialmente da taxa de variação de funções, que podem representar diferentes tipos de processos.

É por isso que a diferenciação permite estudar o processo de mudança, e como comparar variáveis mutáveis, o que tem uma ampla aplicabilidade.

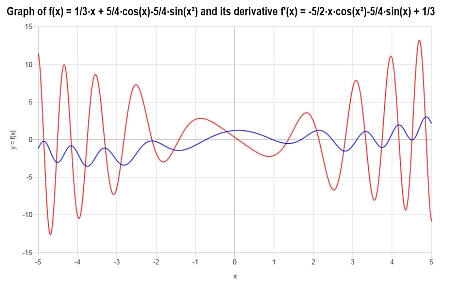
Exemplo: calculando a derivada

Calcule a derivada em relação a x para \(f(x) = \displaystyle \frac{x}{3} + \frac{5}{4} \cos(x) - \frac{5}{4} \sin(x^2)\)

Solução: A seguinte função foi fornecida: \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\), para a qual precisamos calcular sua derivada.

Estado Inicial: Nesse caso, primeiro precisamos simplificar a função dada \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right) \) e, para isso, realizamos as seguintes etapas de simplificação:

Depois de simplificar a função, podemos proceder ao cálculo da derivada:

O seguinte gráfico é obtido para \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\) no intervalo \([-5, 5]\):

Exemplo: diferenciando uma função

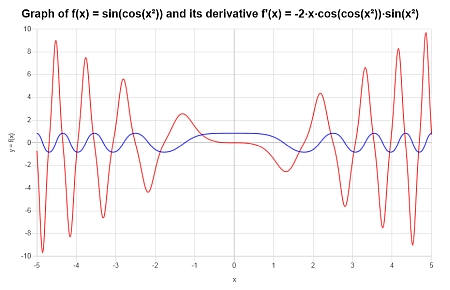
Calcule a derivada de : \(f(x) = \sin(\cos(x^2))\) e forneça o gráfico de \(f(x)\) e \(f'(x)\).

Solução: Agora temos \(\displaystyle f(x)=\sin\left(\cos\left(x^2\right)\right)\).

A função já veio simplificada, então podemos proceder diretamente ao cálculo de sua derivada. Usando esta cal derivada, obtemos:

Portanto, obtemos o seguinte gráfico para a função no intervalo \([-5, 5]\):

Exemplo: calculadora de derivadas

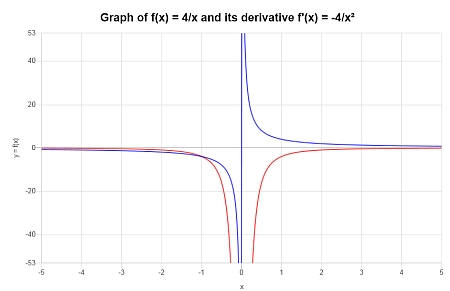
Encontre a derivada de \( f(x) = \displaystyle \frac{4}{x}\). Está bem definido em todos os lugares? Faça um gráfico.

Solução: A função fornecida para a qual a derivada é necessária é \(\displaystyle f(x)=\frac{4}{x}\).

Não há nenhuma simplificação adicional necessária, então podemos prosseguir diretamente para calcular sua derivada:

Graficamente:

Mais sobre derivadas e funções

Esse calculadora derivada com passos será muito útil para você, pois fará o cálculo da derivada de qualquer função dada, mostrando todas as etapas do processo, aplicando as devidas Regras de Derivadas , e informando quando eles estão sendo aplicados e por quê.

Esta calculadora também pode ser chamada calculadora dy dx ou calculadora de quociente diferencial como é exatamente isso que ele faz, ele calcula o limite da razão dy/dx quando dx se aproxima de 0.

Funções são construções extremamente importantes em matemática. Juntamente com a diferenciação, você precisa ser capaz de simplificar uma função geralmente, como um preâmbulo de outros cálculos mais especializados. Existem tipos especiais de funções que permitem realizar operações específicas, como o que você faz com Operações polinomiais .

Curiosamente, muitos elementos importantes, como encontrar as coordenadas do vértice de uma parábola que podem ser derivadas de maneira inteligente usando argumentos geométricos, podem ser obtidas trivialmente usando diferenciação.

Também a ideia de Linha tangente e Aproximação De Primeira Ordem aparecem naturalmente, partindo do conceito de derivada, e uma extensão natural.