Esta calculadora de fórmula vertex

Esta calculadora permitirá aplicar o fórmula do vértice para uma dada função quadrática que você fornece. Esta função quadrática precisa ser válida, como 2x^2 + 3x + 1/3, ou pode vir não simplificada, como 2x^2 - x + 5 - 3/4 x^2 +1/3, etc. função quadrática válida válida fará.

Depois de fornecer uma função quadrática válida, você precisa clicar no botão "Calcular", e as etapas da aplicação da fórmula do vértice serão mostradas, com as etapas seguidas para calcular o vértice da parábola.

As funções quadráticas são muito importantes em aplicações em álgebra e cálculo, e o vértice de uma função quadrática é muito interpretável.

Qual é a fórmula do vértice?

Primeiro, assumimos que começamos com uma função quadrática e a simplificamos para:

\[ f(x) = ax^2 + bx + c \]

Então, a fórmula do vértice para a coordenada x do vértice é:

\[ x_V = \displaystyle -\frac{b}{2a}\]

Como aplicar a fórmula do vértice?

• Passo 1: Identifique a função quadrática em sua forma simplificada. Você precisa ter algo como f(x) = ax²+ bx + c
• Passo 2: A partir da fórmula quadrática, você precisa identificar claramente o que a e b são
• Passo 3: A partir de a e b que você identificou, coloque-os na fórmula xv = -b/2a

Observe que se a = 0, então a fórmula será indefinida, mas neste caso a não será zero, pois temos uma função quadrática, e o termo que multiplica x² não pode ser zero para ser uma função quadrática válida.

Por que é importante encontrar o vértice?

O vértice tem uma propriedade muito importante, que é o ponto onde a função quadrática atinge o mínimo (quando abre para cima quando a > 0) ou é o ponto onde a função quadrática atinge o máximo (quando abre para baixo quando a > 0 ).

Então ao encontrar o vértice já estamos obtendo o ponto extremo da função quadrática.

Exemplo: calcular vértice

Calcule o vértice para a seguinte função quadrática: \(f(x) = 3x^2+3x+2\)

Solução: Precisamos encontrar as coordenadas do vértice da função quadrática \(f(x) = \displaystyle 3x^2+3x+2\).

Para uma função quadrática da forma \(f(x) = a x^2 + bx + c\), a coordenada x do vértice é calculada usando a seguinte fórmula:

\[x_V = \displaystyle -\frac{b}{2a}\]

Nesse caso, temos que a função para a qual precisamos encontrar o vértice é \(f(x) = \displaystyle 3x^2+3x+2\), o que implica que os coeficientes correspondentes são:

\[a = 3\] \[b = 3\] \[c = 2\]

Colocando os valores conhecidos de \(a\) e \(b\) na fórmula para a coordenada x do vértice, obtemos:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 3} = -\frac{1}{2}\]

Agora, precisamos inserir o valor de \(x_V = \displaystyle -\frac{1}{2}\) na função quadrática, então obtemos:

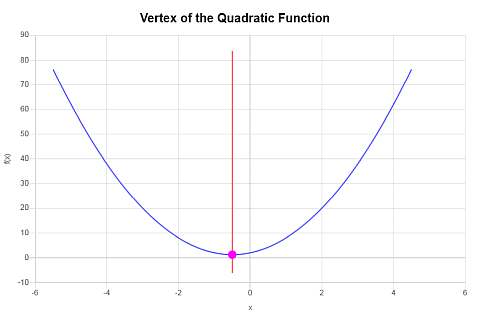
\[y_V = f(x_V)\] \[ = 3\cdot \left(-\frac{1}{2}\right)^2+3\cdot \left(-\frac{1}{2}\right)+2=3\cdot\frac{1}{4}+3\cdot \left(-\frac{1}{2}\right)+2=\frac{3}{4}-\frac{3}{2}+2=\frac{5}{4}\]

Portanto, a coordenada x do vértice é \(x_V = \displaystyle -\frac{1}{2}\) e a coordenada y do vértice é \(y_V = \displaystyle \frac{5}{4}\). Isto, o ponto que representa o vértice é \( \displaystyle \left(-\frac{1}{2}, \frac{5}{4}\right)\).

O seguinte é obtido graficamente:

Exemplo: aplicativo de fórmula vertex

Use a fórmula do vértice para calcular as coordenadas do vértice associado à função \(f(x) = x^2 + 4x - \frac{3}{4}\)

Solução: Mais uma vez, usamos a seguinte fórmula:

\[x_V = \displaystyle -\frac{b}{2a}\]

Desde \(f(x) = \displaystyle x^2+4x-\frac{3}{4}\), o que implica que os coeficientes correspondentes são:

\[a = 1\] \[b = 4\] \[c = -\frac{3}{4}\]

Colocando os valores conhecidos de \(a\) e \(b\) na fórmula para a coordenada x do vértice, obtemos:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{4}{2 \cdot 1} = -2\]

Agora, precisamos inserir o valor de \(x_V = \displaystyle -2\) na função quadrática, então obtemos:

\[y_V = f(x_V)\] \[ = 1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=-2^2+4\cdot \left(-2\right)-\frac{3}{4}=4-8-\frac{3}{4}=-4-\frac{3}{4}=-\frac{19}{4}\]

Portanto, a coordenada x do vértice é \(x_V = \displaystyle -2\) e a coordenada y do vértice é \(y_V = \displaystyle -\frac{19}{4}\). Isto, o ponto que representa o vértice é \( \displaystyle \left(-2, -\frac{19}{4}\right)\).

Isso conclui o cálculo.

Exemplo: aplicativo vertex

Encontre o ponto extremo da função \(f(x) = -2x^2 - 3x + 5\). Esse ponto extremo é um ponto mínimo ou máximo?

Solução: Precisamos encontrar as coordenadas do vértice da função quadrática \(f(x) = \displaystyle -2x^2-3x+5\).

Usamos a seguinte fórmula:

\[x_V = \displaystyle -\frac{b}{2a}\]

Neste caso, temos que a função para a qual precisamos encontrar o vértice é \(f(x) = \displaystyle -2x^2-3x+5\), então:

\[a = -2\] \[b = -3\]

Isso significa que:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{-3}{2 \cdot -2} = -\frac{3}{4}\]

Agora, precisamos inserir o valor de \(x_V = \displaystyle -\frac{3}{4}\) na função quadrática, então obtemos:

\[y_V = f(x_V)\] \[ = \left(-2\right)\cdot \left(-\frac{3}{4}\right)^2+-3\cdot \left(-\frac{3}{4}\right)+5=\left(-2\right)\cdot\frac{9}{16}+-3\cdot \left(-\frac{3}{4}\right)+5=-\frac{9}{8}+\frac{9}{4}+5=\frac{49}{8}\]

Portanto, a coordenada x do vértice é \(x_V = \displaystyle -\frac{3}{4}\) e a coordenada y do vértice é \(y_V = \displaystyle \frac{49}{8}\). Isto, o ponto que representa o vértice é \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\).

Observe que \(a = -2 < 0\), então a parábola tem concavidade voltada para baixo, e o ponto \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\) corresponde a um ponto máximo. Isto é, a função quadrática \(f(x) = \displaystyle -2x^2-3x+5\) atinge um máximo de \( \displaystyle \frac{49}{8}\) em \( x = -\frac{3}{4}\)

Mais calculadoras quadráticas

Muito pode ser feito com funções quadráticas. Você pode calcular o raízes de uma equação quadrática , você pode encontre o eixo de simetria de uma função quadrática, e assim por diante.

Aplicando o fórmula do vértice está intimamente ligada à aplicação do Fórmula quadrática e a Eixo de simetria .