Grafico polinomiale

Usa questa calcolatrice se hai bisogno di aiuto per rappresentare graficamente una funzione polinomiale. Il processo è semplice: devi solo digitare la funzione polinomiale che vuoi rappresentare graficamente. Puoi scrivere qualcosa come '3x^3 + x - 1', oppure puoi premetterlo con il nome della funzione, come 'p(x) = 3x^3 + x - 1'.

I coefficienti del polinomio fornito non devono necessariamente essere interi, possono essere frazioni o qualsiasi espressione algebrica valida. Il polinomio che fornisci può essere semplificato o meno, non importa.

Quindi, una volta fornito il polinomio, puoi facoltativamente determinare gli intervalli di valori x che verranno rappresentati graficamente, quindi fai clic su "Calcola" e, in breve, verranno mostrati tutti i passaggi del processo.

funzioni polinomiali sono uno degli oggetti più importanti che troverai in Algebra così come in Calculus. Inoltre, i polinomi portano alla necessità di risolvere equazioni polinomiali, che hanno un sacco di applicazioni ovunque, in ogni aspetto della vita, anche oltre la matematica.

Cenni alle funzioni polinomiali

Ricordiamo che una funzione polinomiale ha la seguente forma:

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

dove assumiamo che \(a_n \ne 0\), e diciamo che the grado di polinomio in questo caso è uguale a \(n\), e il coefficiente principale è \(a_n\). Il modo profano di definire il grado di un polinomio è che corrisponde alla massima potenza presente nell'espressione polinomiale.

Ad esempio, \(p(x) = 3x^2 + 2x - 1\) è un polinomio di grado 2 e il suo coefficiente principale è 3. Ora, \(p(x) = \sin(3x^2 + 2x - 1)\) NON è un polinomio, per esempio.

Come fare i grafici dei polinomi?

La rappresentazione grafica dei polinomi in linea di principio mostra la stessa cosa della rappresentazione grafica di qualsiasi altra funzione. Se dovessi farlo a mano, tabuleresti diversi valori per x e y e tracceresti una curva che passerebbe più o meno attraverso i punti che stai ottenendo nella tua tabella.

Naturalmente, questo metodo è un po' primitivo, perché in generale non possiamo necessariamente conoscere il grafico completo di una funzione conoscendo solo un mucchio di punti che stiamo tabulando.

Fortunatamente, per i polinomi il compito è un po' più facile, e in realtà possiamo sapere molto sul suo grafico conoscendo il suo coefficiente principale e il suo grado.

Passaggi per la rappresentazione grafica di funzioni polinomiali

Il grafico di un polinomio dipende in ultima analisi dal coefficiente specifico di ogni polinomio. Ma possiamo fare alcune affermazioni forti sul comportamento finale di un polinomio e sull'esistenza di radici reali.

Ricordiamo che il comportamento finale di un polinomio è il comportamento del polinomio quando x è molto grande e negativo, e quando x è molto grande e positivo.

• Fase 1: Identifica la funzione polinomiale e semplifica se puoi, poiché è più facile rappresentare graficamente espressioni semplificate
• Passo 2: Conosci le radici del polinomio? Se quelle sono radici reali, conosci i punti in cui il polinomio attraversa l'asse x, il che ti dà un forte riferimento grafico
• Smusso 3: Se il grado del polinomio è dispari, allora il comportamento finale sarà opposto per grandi valori x negativi e grandi valori x positivi. Se il coefficiente principale è positivo, per grandi valori x negativi il polinomio sarà molto grande e negativo, e per grandi valori x positivi il polinomio sarà molto grande e positivo. Se il coefficiente principale è negativo, per grandi valori x negativi il polinomio sarà molto grande e positivo, e per grandi valori x positivi il polinomio sarà molto grande e negativo
• Passaggio 4: Se il grado del polinomio è pari, il comportamento finale sarà lo stesso per grandi valori x negativi e grandi valori x positivi. Se il coefficiente principale è positivo, per grandi valori x negativi e positivi il polinomio sarà molto grande e positivo. Se il coefficiente principale è negativo, per grandi valori x negativi e positivi il polinomio sarà molto grande e negativo
• Passaggio 5: Se il grado del polinomio è dispari, il polinomio attraverserà almeno una volta l'asse x (quindi ha almeno una radice reale), mentre per un grado pari il polinomio non attraverserà necessariamente l'asse x
• Passaggio 6: Un polinomio di grado n attraverserà l'asse x al massimo n volte. Ad esempio, un polinomio di 4 grado 4 può attraversare l'asse x al massimo 4 volte

Quindi, ad esempio, un polinomio cubico può attraversare l'asse x al massimo 3 volte, ma non è necessario.

Calcolatrice grafica

Quali sono i vantaggi dell'utilizzo di una calcolatrice grafica? Molti. Questo non vuol dire che non sia una buona abilità avere quella di essere in grado di abbozzare accuratamente un polinomio usando carta e penna.

\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]

• Vantaggio 1: Ti assicuri di ottenere una rappresentazione accurata del grafico effettivo del polinomio
• Vantaggio 2: Puoi usarlo per controllare il tuo lavoro, per assicurarti di aver seguito i passi giusti
• Vantaggio 3: Una buona calcolatrice sceglie una finestra appropriata per mostrare gli aspetti più rilevanti del grafico

Un buon grafico può dirti molto sulle proprietà di una funzione, e lo stesso vale per un polinomio. La rappresentazione grafica dei polinomi può aiutarti a visualizzare veramente quale tipo di radici ha il polinomio.

Suggerimenti e trucchi

Fai attenzione con la lettura eccessiva di ciò che vedi in un grafico polinomiale. Non puoi facilmente dire molto sulle radici con molteplicità, quindi nulla sostituisce la funzione effettiva.

Se vuoi provare altri tipi di funzioni, prova questo grafico delle funzioni attrezzo.

Esempio: rappresentazione grafica di funzioni polinomiali

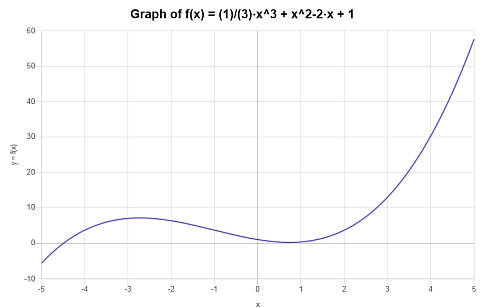
Rappresentare graficamente il seguente polinomio: \(p(x) = \frac{1}{3} x^3 + x^2- 2x +1 \)

Soluzione: Ci viene fornita la seguente espressione polinomiale che dobbiamo calcolare: \(\displaystyle \frac{1}{3} x^3 + x^2- 2x +1\).

L'espressione fornita è irriducibile, quindi non c'è nulla da semplificare.

Si ottiene il seguente grafico per la data espressione polinomiale sull'intervallo \([-5, 5]\):

Esempio: grafico polinomiale

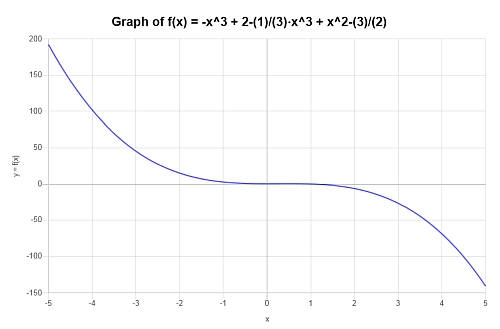
Semplificare e rappresentare graficamente: \(p(x) = x^4 - x^3 + 2 - \frac{1}{3}x^3 + x^2 - \frac{3}{2}\)

Soluzione: Ora dobbiamo lavorare con: \(\displaystyle -x^3+2-\frac{1}{3}x^3+x^2-\frac{3}{2}\).

Si ottiene la seguente semplificazione:

che conclude il processo di semplificazione polinomiale.

Quindi, si ottiene il seguente grafico per \(\displaystyle -\frac{4}{3}x^3+x^2+\frac{1}{2}\) sull'intervallo \([-5, 5]\):

Esempio: più grafici polinomiali

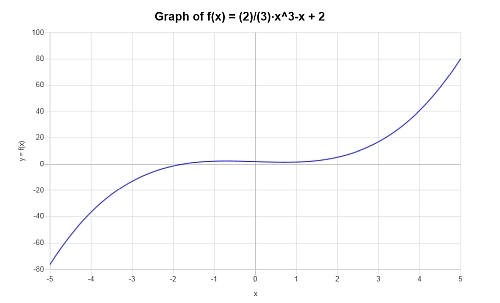
Trova il grafico del seguente polinomio \( p(x) = \frac{2}{3} x^3 - x +2 \).

Soluzione: Per questo esempio, il polinomio fornito è: \(\displaystyle \frac{2}{3} x^3 - x +2 \).

In questo caso, l'espressione fornita è irriducibile, quindi non c'è nulla da semplificare.

Si ottiene il seguente grafico per la data espressione polinomiale sull'intervallo \([-5, 5]\):

Altri calcolatori polinomiali

La rappresentazione grafica dei polinomi è estremamente utile in quanto ci mostra le principali caratteristiche del loro comportamento attorno alle loro radici e il loro comportamento finale. La rappresentazione grafica di solito va di pari passo con l'identificazione approssimativa di dove potrebbero essere le radici, con cui potrebbero essere utilizzate fattorizzazione di polinomi anche.

Anche se possiamo sapere molto sul polinomio solo rappresentandolo graficamente, dobbiamo ancora passare attraverso il processo del tentativo di trovare radici razionali , come punto di partenza per risoluzione di equazioni polinomiali con grado superiore a 2 (questo, quello no equazioni quadratiche ).

Indovinare sistematicamente o trovare radici razionali, in coppia con l'uso Divisione Lunga o Divisione sintetica quindi per usare il teorema dei fattori può portare a una ricerca di successo di radici polinomiali , ma tale approccio non funziona sempre e spesso è necessario fare affidamento sulla calcolatrice per trovare approssimazioni numeriche.