Test de la ligne horizontale

Cette calculatrice vous permettra d'effectuer le test de la ligne horizontale pour toute fonction donnée, en indiquant les étapes. La fonction que vous fournissez peut être quelque chose comme "y = 2x - 1", qui est le type de fonction le plus simple fonction linéaire que vous pouvez trouver, ou vous pouvez fournir une fonction plus complexe comme "y = (2x-1)/(x+1)" qui implique un fonction rationnelle .

Une fois que vous avez fourni une fonction valide, vous pouvez cliquer sur le bouton "Calculer" et vous obtiendrez toutes les étapes du processus, en indiquant si la fonction passe ou non le test de la ligne horizontale (HLT).

Cette calculatrice fonctionne en définissant une ligne horizontale générique et en vérifiant combien de fois (le cas échéant) la ligne croise cette ligne horizontale arbitraire. Cela implique Résoudre pour x l'équation y = f(x).

Qu'est-ce que le test de la ligne horizontale ?

Le HLT est un test qui permet d'évaluer si une fonction est biunivoque ou non. Il consiste à tracer des lignes horizontales à différentes hauteurs et à voir où elles croisent le graphique de la fonction donnée f(x), si elles le croisent.

Si aucune ligne horizontale que vous pouvez imaginer ne traverse plus d'une fois le graphique de la fonction f(x), alors la fonction est biunivoque . En revanche, si vous êtes capable de trouver une ligne horizontale qui traverse le graphique de la fonction f(x) PLUS D'UNE FOIS, alors vous avez prouvé que la fonction n'est PAS biunivoque

Cet outil ne permet pas de prouver qu'une fonction est biunivoque à l'aide du test de la ligne horizontale, mais plutôt de prouver qu'elle n'est pas biunivoque à l'aide de ce test.

Parce que, en pratique, je ne peux pas représenter TOUTES les lignes horizontales existantes pour vérifier combien de fois elles croisent le graphique de f(x), mais si je trouve UNE ligne horizontale qui croise le graphique de f(x) trop de fois, alors je sais qu'elle n'est pas biunivoque. Donc, bonne réflexion, tu es sur une bonne piste.

Utilisation du test de la ligne horizontale dans la pratique

Par exemple, si vous avez la fonction \(f(x) = x^2\), le graphique ressemblera plus ou moins à ceci :

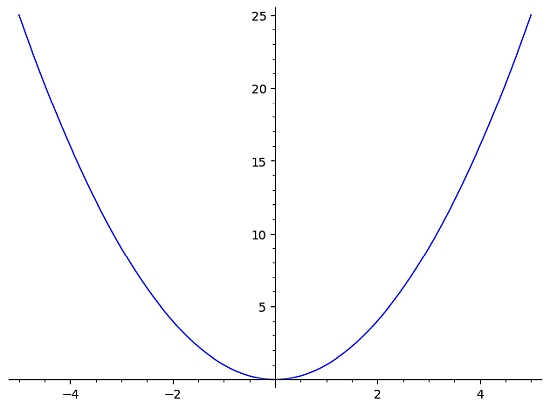
Dans ce cas, nous voyons tout de suite que cette fonction échoue au test de la ligne horizontale. En effet, la ligne horizontale y = 10 représentée dans le graphique ci-dessous croise le graphique de f(x) deux fois (plus d'une fois)

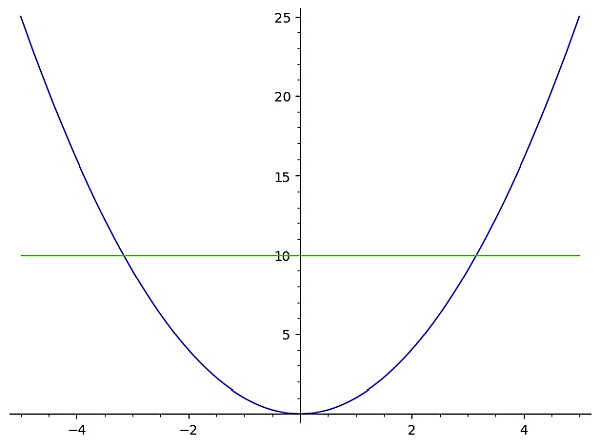
Dans ce cas, la fonction \(f(x) = x^2\) échoue au test de la ligne horizontale et n'est donc pas une fonction univoque .

Puisqu'il est impossible de tester TOUTES les lignes horizontales possibles, le HLT doit essayer d'utiliser des moyens algébriques, à moins que vous ne voyiez visuellement un cas clair de ligne horizontale qui ferait échouer la fonction au test.

Utiliser le test de la ligne horizontale (de manière analytique)

• Étape 1 : A partir d'une fonction valide donnée f(x), vous fixerez le niveau d'une ligne horizontale à une valeur arbitraire de y
• Étape 2 : On pose donc l'équation : y = f(x), et l'objectif est de résoudre x
• Étape 3 : Il n'existe pas de stratégie unique pour résoudre cette équation la résolution de l'équation dépend de la nature de la fonction f(x). Si f(x) est une fonction linéaire ou quadratique simple, il est assez facile de résoudre x. Si ce n'est pas le cas, il faut tester différentes méthodes
• Étape 4 : Si, en résolvant x, vous trouvez plus d'une solution pour un y arbitraire, la fonction échoue au test HLT. Dans le cas contraire, s'il n'y a qu'une seule solution ou aucune solution, la fonction est acceptée.

La soustraction de fractions est simplement dérivée de la somme des fractions : Pour soustraire deux fractions, il suffit de multiplier la seconde par -1, puis de l'ajouter à la première .

La ligne horizontale peut-elle prendre des valeurs négatives ou positives ?

La principale caractéristique de la mise en œuvre analytique de la HLT est que vous choisissez une ligne horizontale arbitraire. Il peut s'agir d'une valeur arbitraire, positive ou négative. Ensuite, la valeur arbitraire de y utilisée MAI détermine si les solutions proposées sont bien définies ou non, mais cela n'AJOUTE pas plus de solutions, cela peut potentiellement soustraire des solutions à la place.

Par exemple, si vous commencez par \(f(x)= \frac{2x+1}{x-1}\), et que vous résolvez x comme suit : \(y = \frac{2x+1}{x-1}\), vous obtiendrez

\(x = \frac{y+1}{y-2}\)

ce qui signifie que pour un \(y\) donné, vous avez AU PLUS une solution. Pourquoi une solution au plus ? Parce que lorsque y = 2, il n'y a en fait aucune solution, et pour tout autre y, il y a une solution. Cela permet de montrer que la fonction passe le test de la ligne horizontale.

Exemple : passage de la hlt

La fonction suivante passe-t-elle la HLT : \(f(x) = \frac{1}{3} x + \frac{5}{4}\) ?

Solution :

La fonction fournie est la suivante :

\[f\left(x\right) = \frac13x+\frac54\]

Ensuite, afin d'évaluer si la fonction donnée passe ou non le test de la ligne horizontale, nous devons résoudre \(x\) et déterminer s'il n'y a pas de solution, une solution ou plusieurs solutions. L'équation de départ est la suivante

\[y=\frac{1}{3}x+\frac{5}{4}\]

Résolution de l'équation linéaire

En plaçant \(x\) du côté gauche et \(y\) et la constante du côté droit, nous obtenons

\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]

Maintenant, en résolvant \(x\), en divisant les deux côtés de l'équation par \(-\frac{1}{3}\), on obtient ce qui suit

\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]

et en simplifiant on obtient finalement ce qui suit

\[\displaystyle x=3y-\frac{15}{4}\]

Par conséquent, la résolution de \(x\) pour une équation linéaire donnée conduit à \(x = 3y-\frac{15}{4}\).

Nous constatons qu'en résolvant \(x\), nous trouvons une solution et qu'il s'agit d'une seule solution, la fonction donnée passe le test de la ligne horizontale.

Résultats du test de la ligne horizontale

Sur la base des travaux présentés ci-dessus, on peut conclure que la fonction donnée passe le test de la ligne horizontale.

Graphiquement, la situation peut être décrite comme suit :

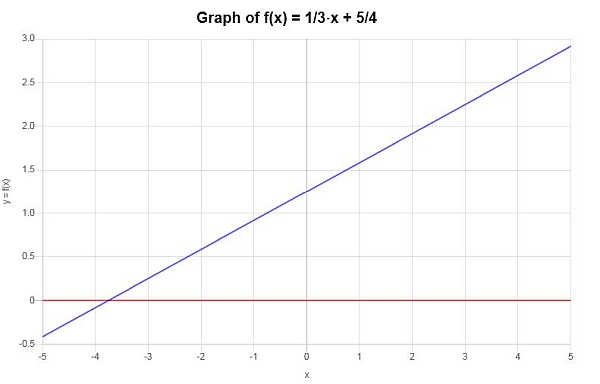
Exemple : s'agit-il d'une fonction "one-to-one" ?

En utilisant le test de la ligne horizontale, indiquez si la fonction suivante est biunivoque : \(f(x) = x^3 - 1\)

Solution : Afin d'évaluer si la fonction donnée passe ou non le test de la ligne horizontale, nous devons résoudre l'équation \(y = x^3 - 1\) pour \(x\) et déterminer s'il n'y a pas de solution, une solution ou plusieurs solutions.

Étape Initiale : Dans ce cas, nous devons d'abord simplifier l'équation donnée, et pour ce faire, nous procédons aux étapes de simplification suivantes :

Nous obtenons alors les solutions :

\[x_1=\left(y+1\right)^{\frac{1}{3}} \] \[x_2=\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}-1\right) \] \[x_3=-\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}+1\right) \]

Parmi ces solutions, nous n'avons qu'une seule solution réelle, qui est \(x_1=\left(y+1\right)^{\frac{1}{3}}\). Par conséquent, et puisqu'en résolvant \(x\) nous trouvons une solution et qu'il s'agit d'une seule solution réelle, la fonction donnée réussit le test de la ligne horizontale.