En savoir plus sur les fonctions linéaires

Cette calculatrice de fonction linéaire vous permettra de calculer un fonction linéaire en fournissant certaines informations requises sur la fonction.

Il existe plusieurs façons de le faire. Vous pouvez soit (1) fournir une équation linéaire en x et y qui peut être résolue pour y, soit (2) fournir directement l'expression pente et Interception O ou (3) vous pouvez fournir la pente et un point où la ligne passe, ou (4) vous pouvez fournir 2 points où la ligne passe.

Quelles informations allez-vous fournir ? Cela dépend en grande partie des informations dont vous disposez, et cela dépendra du cas spécifique.

Un cas courant est de trouver une fonction linéaire qui passe par deux points donnés, mais les autres façons de déterminer la droite sont également courantes.

Qu'est-ce qu'une fonction linéaire ?

La réponse dépend du nombre de variables que vous considérez, mais pour une variable x, une fonction linéaire est une fonction de la forme

\[f(x) = a + b x \]

Juste une technicité, en maths plus avancées, c'est une fonction linéaire affine, et elle n'est pas strictement linéaire sauf si a = 0, mais cette idée dépasse le cadre de cette présentation. Pour nous, \(f(x) = a + b x \) est une fonction linéaire en x.

La valeur de a dans \(f(x) = a + b x \) est connue comme la Interception O et b est connu comme le pente . Vous verrez parfois la convention \(f(x) = mx + n \), où m est la pente et n l'ordonnée à l'origine.

Mais c'est une convention de nom, il suffit de se rappeler que la constante qui multiplie la variable x est la pente, et l'autre est l'ordonnée à l'origine. Pourquoi cela ? Parce que lorsque x = 0, on obtient \(f(0) = m \cdot 0 + n = n\), ce qui indique que n est précisément l'ordonnée à l'origine.

Quelles sont les étapes du calcul d'une fonction linéaire ?

• Étape 1 : Identifiez le type d'informations que vous avez fournies
• Étape 2 : Si les informations dont vous disposez sont une équation linéaire en x et y, vous devez résoudre y et vous obtenez automatiquement la fonction linéaire f(x) = y
• Étape 3 : Si vous avez la pente b et l'ordonnée à l'origine a, alors la fonction linéaire est directement f(x) = a + b x
• Étape 5 : Si vous avez deux points \((x_1, y_1)\) et \((x_2, y_2)\) par lesquels passe la droite, alors vous pouvez utiliser la formule : \(\displaystyle f(x) = y_1 + \left(\frac{y_2-y_1}{x_2-x_1} \right)(x-x_1)\) pour la fonction linéaire
• Étape 6 : Si à la place vous avez un point \((x_1, y_1)\) par lequel passe la droite et la pente, alors vous pouvez utiliser la formule : \(\displaystyle f(x) = y_1 + m(x-x_1)\) pour la fonction linéaire

La liste d'étapes ci-dessus est exhaustive et prend en compte tous les cas possibles. Ultimement, la situation la plus simple et la moins impliquée correspond au cas où la pente et l'ordonnée à l'origine sont connues, où nous pouvons calculer le Forme d'interception de pente immédiatement, mais ce n'est pas toujours le cas.

Quelle est la formule de la fonction linéaire

En fin de compte, et indépendamment des informations que vous avez fournies, vous pouvez arriver à la formule de la fonction linéaire connue sous le nom de forme de l'ordonnée à l'origine de la pente, qui est :

\[y = a + bx \]

Maintenant, puisque vous définissez une fonction, vous pouvez aussi écrire \(f(x) = a + b x\).

Quelles sont les étapes pour trouver la formule de la fonction linéaire ?

• Étape 1 : Identifier les informations fournies
• Étape 2 : trouver la formule correspondante y = a + bx, en identifiant la pente b et l'ordonnée à l'origine a
• Étape 3 : Remplacer y par f(x) et écrire f(x) = a + bx

Géométriquement, le graphique de la fonction linéaire sera une ligne qui coupe effectivement l'axe des y au point (0, a), et la pente b reflétera le degré d'inclinaison de la ligne.

Pourquoi est-il utile de calculer des fonctions linéaires ?

La relation linéaire entre les variables est très courante dans de nombreuses applications, il devient donc indispensable de bien comprendre le fonctionnement des fonctions linéaires.

Et nous pouvons également définir des fonctions linéaires pour davantage de variables, ce qui en fait un objet encore plus puissant.

Exemple : calculateur de fonctions linéaires

Calculez l'équation de la fonction linéaire qui passe par les points : \( (\frac{22}{3}, \frac{7}{4})\) et \((-1, \frac{5}{6})\)

Solution: L'objectif principal est de construire une fonction linéaire sur la base des informations fournies, si possible.

L'information fournie sur la ligne est que la ligne passe par les points\(\displaystyle \left( \frac{22}{3}, \frac{7}{4}\right)\) et \(\displaystyle \left( -1, \frac{5}{6}\right)\)

Par conséquent, la première étape consiste à calculer la pente. La formule de la pente est : \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} \]

Maintenant, en branchant les nombres correspondants est , on obtient que la pente est : \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle \frac{5}{6} - \frac{7}{4}}{ \displaystyle -1 - \frac{22}{3}} = \frac{ \displaystyle \frac{5}{6}-\frac{7}{4}}{ \displaystyle -1-\frac{22}{3}} = \frac{11}{100}\]

Alors, maintenant nous savons que la pente est \(\displaystyle m = \frac{11}{100}\) et que la droite passe par le point \(\displaystyle \left( \frac{22}{3}, \frac{7}{4}\right)\)

Par conséquent, avec les informations dont nous disposons, nous pouvons construire directement la forme point-pente de la ligne, qui est

\[\displaystyle y - y_1 = b \left(x - x_1\right)\]

puis en branchant les valeurs connues de \(\displaystyle b = \frac{11}{100}\) et \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{22}{3}, \frac{7}{4}\right)\), on obtient que

\[\displaystyle y-\frac{7}{4} = \frac{11}{100} \left(x-\frac{22}{3}\right)\]

Maintenant, nous devons développer le côté droit de l'équation en distribuant la pente, nous obtenons donc \[\displaystyle y = \frac{11}{100} x + \frac{11}{100} \left(-\frac{22}{3}\right) + \frac{7}{4}\]

et en simplifiant on obtient que \[\displaystyle y=\frac{11}{100}x+\frac{283}{300}\]

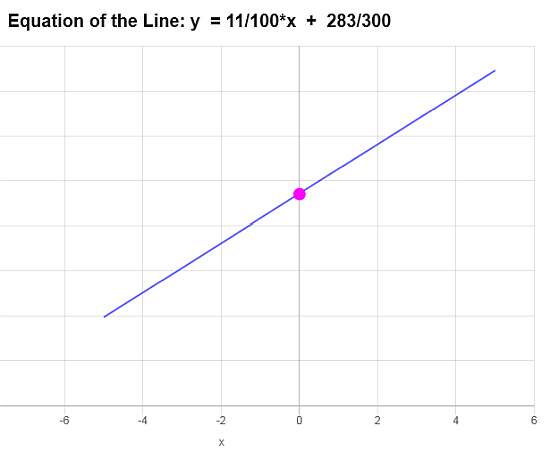
Conclusion : D'après les données fournies, nous concluons que l'équation de la droite est \(\displaystyle f(x)=\frac{11}{100}x+\frac{283}{300}\), et qu'elle correspond à une droite dont la pente est \(\displaystyle b = \frac{11}{100}\) et l'ordonnée à l'origine \(\displaystyle a = \frac{283}{300}\).

D'après ces informations, le graphique est :

Exemple : un autre calcul de fonction linéaire

Calculer la fonction linéaire associée à : \(\frac{1}{3}x + \frac{5}{4}y - \frac{5}{6} = 0\)

Solution:

Maintenant, pour cet exemple, la façon dont nous avons défini une fonction linéaire est via une équation linéaire générale, donnée par :

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y-\frac{5}{6}=0\]

Nous pouvons simplifier les constantes :

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y-\frac{5}{6}=0\]

Maintenant, en mettant \(y\) sur le côté gauche et \(x\) et la constante sur le côté droit, on obtient

\[\displaystyle \frac{5}{4}y = -\frac{1}{3}x + \frac{5}{6}\]

Maintenant, en résolvant pour \(y\), en divisant les deux côtés de l'équation par \(\frac{5}{4}\), on obtient ce qui suit

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{5}{6}}{\frac{5}{4}}\]

et en simplifiant on obtient finalement ce qui suit

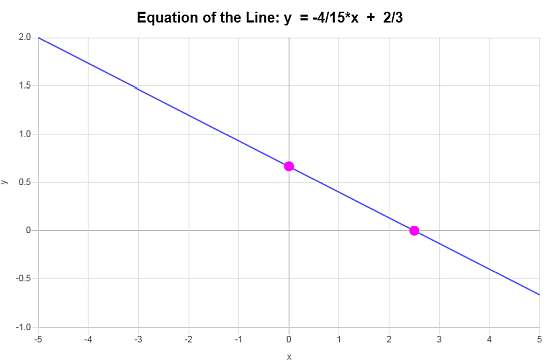
\[\displaystyle y=-\frac{4}{15}x+\frac{2}{3}\]

Conclusion : Maintenant, nous pouvons dire que d'après les données fournies, la conclusion est que l'équation de la ligne est \(\displaystyle f(x)=-\frac{4}{15}x+\frac{2}{3}\), et qu'elle correspond à une ligne avec une pente de \(\displaystyle b = -\frac{4}{15}\) et un ordonnée à l'origine de \(\displaystyle a = \frac{2}{3}\).

D'après ces informations, le graphique est :

Exemple : autres calculateurs de fonctions linéaires

Calculez la fonction linéaire dont la pente est m = 0 et qui coupe l'axe des y au point (0, 4).

Solution: Dans ce cas, nous avons donné la pente, qui est m = 0, et l'ordonnée à l'origine, qui est (0, 4). Puisque la pente est 0, la ligne est horizontale, donc dans ce cas, l'équation de la ligne est \(f(x) = 4\).

Plus de calculateurs de fonctions linéaires

Les calculatrices intéressantes sont la calculatrice de pente et la calculatrice d'ordonnée à l'origine. Vous pouvez également être intéressé par trouver la ligne perpendiculaire à une ligne donnée .

Une autre forme courante de la ligne est le formes standard et vous pouvez certainement passer d'une forme à l'autre.