Calculatrice de fonctions inverses
Instructions : Utilisez cette calculatrice pour trouver la fonction inverse d'une fonction que vous fournissez, en montrant toutes les étapes. Veuillez saisir l'expression de la fonction dont vous souhaitez trouver l'inverse dans la case ci-dessous.
En savoir plus sur cette calculatrice de fonctions inverses
Cette calculatrice vous permettra de trouver l'inverse d'une fonction donnée en montrant toutes les étapes, en supposant que l'inverse existe. La calculatrice examinera la fonction résoudre une équation associé à la définition de la fonction, et il essaiera de déterminer s'il existe ou non un inverse.
Par exemple, vous pouvez fournir une fonction linéaire comme "f(x) = 3x - 2", ce qui serait un cas simple, ou vous pouvez aller plus loin avec quelque chose d'un peu plus difficile, comme avec une fonction rationnelle comme "y = (x-1)/(x-3)".
Une fois que vous avez fourni une fonction valide, cliquez sur le bouton "Calculer" pour que toutes les étapes du processus vous soient montrées, avec la fonction inverse comme réponse finale, si une fonction inverse existe, ou avec l'explication qu'aucune solution n'a pu être trouvée et pourquoi.
Il n'est pas garanti que vous trouverez toutes les fonctions inverses. D'une part, toutes les fonctions n'ont pas d'inverse, et d'autre part (comme nous le verrons dans la section suivante), le processus de recherche de l'inverse implique Résoudre pour x pour une équation et, comme nous le savons, certaines équations peuvent être très difficiles, voire impossibles à résoudre.
Ainsi, les fonctions les plus simples sont plus susceptibles de permettre la recherche de leur inverse, si celui-ci existe.

Comment définir l'inverse d'une fonction ?
En termes simples, l'inverse d'une fonction est la fonction qui fait le contraire de ce que fait la fonction originale. Vous pouvez donc considérer une fonction comme y = f(x), et l'envisager comme un passage de x à y. Vous alimentez la fonction avec un x, et la fonction vous donne un y spécifique.
La fonction inverse part de y et revient à x, de manière à ce que x soit le même que celui qui a conduit à y par le biais de la fonction d'origine. La définition formelle se fait par composition de la fonction . Pour une fonction \(f\), on dit que \(g\) est la fonction inverse de \(f\) si
\[ f(g(x)) = x \]et
\[ g(f(x)) = x \]pour tout x dans un certain ensemble. Il y a plus, mais nous en resterons au niveau intuitif (au sens strict, une fonction doit être injective et surjective pour être inversible, et d'autres détails techniques sont à prendre en compte, comme la restriction de l'expression "injective" à l'expression "surjective") domaine et portée , etc.)
Habituellement, nous appelons \(f^{-1}\) l'inverse de \(f\), de sorte que la formule qui définit l'inverse s'écrit typiquement comme suit :
\[ f(f^{-1}(x)) = x \]Quelles sont les étapes pour trouver la fonction inverse
- Étape 1 : Commencez par l'équation qui définit la fonction, c'est-à-dire que vous commencez par y = f(x)
- Étape 2 : Vous utilisez ensuite la manipulation algébrique pour résoudre x. En fonction de la complexité de f(x), vous pouvez trouver plus ou moins facile de résoudre x.
- Étape 3 : Dans certaines circonstances, vous ne serez tout simplement pas en mesure de résoudre x, pour les fonctions non linéaires complexes f(x)
- Étape 4 : Si vous êtes capable de résoudre x, vous devriez pouvoir écrire x = g(y)
- Étape 5 : Vous devez déterminer si la solution trouvée est unique. C'est-à-dire qu'elle peut résoudre x de manière unique. En d'autres termes, avez-vous trouvé une seule solution en résolvant x ? Si oui, vous avez une fonction inverse, sinon, il n'y a pas d'inverse
- Étape 6 : Si vous avez trouvé l'inverse en résolvant x = g(y), il vous suffit de changer le nom de la variable et d'écrire f -1 (x) = g(x), ce qui met l'accent sur le fait que g(x) EST l'inverse réel
Si vous deviez utiliser le calcul et les dérivés (mais notez que vous n'avez pas besoin de Produits dérivés pour calculer l'inverse), vous pouvez trouver la dérivée de la fonction et vous assurer que la dérivée est toujours positive ou négative, afin de garantir que la fonction est injective, et donc inversible.
Mais en général, la méthodologie de l Résoudre pour x est beaucoup plus acceptable pour les étudiants en algèbre de base.
Règle de recherche des fonctions inverses
Il n'existe en fait aucune autre règle pour calculer la fonction inverse, si ce n'est de commencer par y = f(x) et de résoudre ensuite pour x. Une telle règle semble assez large, car elle l'est. Plus qu'une règle, il s'agit d'une méthodologie générique pour démarrer le processus.
En fin de compte, le calcul de l'inverse dépendra de votre capacité à résoudre une équation et à vous assurer que cette solution est unique. Il est utile d'évaluer le graphique de la fonction au préalable, afin de ne pas chercher un inverse lorsqu'il n'y en a manifestement pas.
Que faut-il chercher dans un graphique ? Une fonction doit être monotone (croissante ou décroissante) sur un certain sous-domaine pour être inversible. Ceci étant dit, nous pourrions commodément restreindre le domaine d'une fonction à un sous-domaine plus petit afin de trouver l'inverse dans un ensemble plus petit, ce qui est toujours possible.

Comment pouvons-nous être sûrs que la fonction a une inverse ?
Formellement, la seule façon de s'assurer qu'une fonction a un inverse est de s'assurer que la fonction est injective (1 à 1). Pour ce faire, on calcule sa dérivée (si elle existe) et on s'assure qu'elle est positive et négative partout, ou on s'assure manuellement que lorsque l'on commence par y = f(x) et que l'on résout pour x, on obtient toujours une solution unique.
Ceci peut également être vu graphiquement, en utilisant le test de la ligne horizontale : Vous tracez une ligne horizontale arbitraire, et la fonction f(x) passe le test de la ligne horizontale si toute ligne horizontale tracée croise le graphique de la fonction au plus une fois.

Exemple : recherche de la fonction inverse
Trouvez l'inverse de la fonction suivante : \(f(x) = \displaystyle \frac{1}{3} x + \frac{5}{4}\)
Solution :
Nous avons la fonction suivante :
\[f(x) = \frac{1}{3} x + \frac{5}{4}\]Ensuite, pour trouver l'inverse de la fonction donnée, nous devons résoudre \(x\) et déterminer s'il y a une solution ou non. L'équation de départ est la suivante :
\[y = \displaystyle \frac{1}{3}x+\frac{5}{4}\]Étape 0 : Dans ce cas, nous devons d'abord simplifier l'équation linéaire donnée, et pour ce faire, nous procédons aux étapes de simplification suivantes :
Résolution de l'équation linéaire
En plaçant \(x\) du côté gauche et \(y\) et la constante du côté droit, nous obtenons
\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]Maintenant, en résolvant \(x\), en divisant les deux côtés de l'équation par \(-\frac{1}{3}\), on obtient ce qui suit
\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]et en simplifiant on obtient finalement ce qui suit
\[\displaystyle x=3y-\frac{15}{4}\]Par conséquent, la résolution de \(y\) pour une équation linéaire donnée conduit à \(x=3y-\frac{15}{4}\).
Par conséquent, et puisqu'en résolvant \(x\) nous trouvons une solution et qu'il s'agit d'une seule solution, nous avons trouvé l'inverse.
La fonction inverse
Sur la base des travaux présentés ci-dessus, on peut conclure que la fonction inverse est :
\[f^{-1}(x) = 3x-\frac{15}{4}\]La fonction inverse peut être représentée graphiquement comme suit :
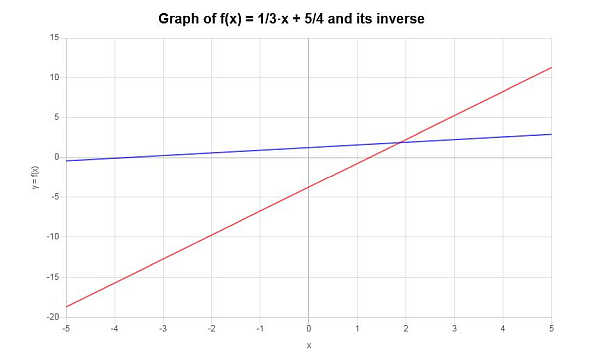
Exemple : autres exemples inverses
Calculer la fonction inverse de : \(y = \frac{x-1}{x+3}\)
Solution :
Pour trouver l'inverse de la fonction donnée, nous résolvons \(x\) et déterminons s'il existe une solution ou non. L'équation de départ est la suivante :
\[y=\frac{x-1}{x+3}\]On obtient le résultat suivant :
Équation du numérateur auxiliaire
Nous devons fixer le numérateur à zéro et trouver les solutions. Ensuite, les racines qui ne rendent pas le dénominateur égal à zéro seront des solutions de l'équation rationnelle
La manipulation algébrique de l'équation polynomiale ci-dessus permet d'obtenir le résultat suivant :
\[x = -\frac{3y+1}{y-1} \]Équation du dénominateur auxiliaire
Nous trouvons les racines du dénominateur : \(x+3=0\)
Par conséquent, la résolution de \(x\) pour une équation linéaire donnée conduit à \(x=-3\).
Assembler les solutions d'une équation rationnelle
Ensuite, en vérifiant que nous n'avons pas de zéro au dénominateur, nous trouvons l'ensemble de solutions suivant à l'équation \(\displaystyle y=\frac{x-1}{x+3}\) est
\[x = -\frac{3y+1}{y-1} \]Puisque lorsque nous résolvons \(x\) nous trouvons une et une seule solution, nous concluons que nous avons une fonction inverse.
Recherche de la fonction inverse
Sur la base des travaux présentés ci-dessus, on peut conclure que la fonction inverse est :
\[f^{-1}(x) = -\frac{3x+1}{x-1}\]La fonction inverse trouvée peut être représentée graphiquement comme suit :
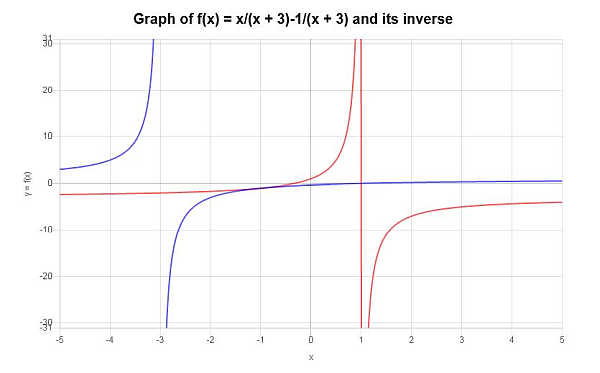
Exemple : toutes les fonctions n'ont pas d'inverse
La fonction suivante a-t-elle un inverse ? \( y = \displaystyle \frac{1}{3} x^2 - \frac{2}{5} \) ?
Solution : Observez que
\[ y =\displaystyle \frac{1}{3} x^2 - \frac{2}{5} \] \[ \displaystyle \Rightarrow y + \frac{2}{5} = \frac{1}{3} x^2 \] \[ \displaystyle\Rightarrow x^2 = 3\left(y + \frac{2}{5} \right) \] \[\displaystyle \Rightarrow x = \pm \sqrt{ 3\left(y + \frac{2}{5} \right) }\]ce qui indique qu'il y a deux solutions, et donc qu'il n'y a pas d'inverse dans ce cas.
Plus de calculatrices de fonctions
Les fonctions sont un objet crucial en mathématiques, en particulier en calcul et en algèbre, où de nombreuses associations entre les variables sont établies par le biais de fonctions.
Il y a beaucoup de choses que vous pouvez faire avec une fonction : vous pouvez les simplifier vous pouvez différencier une fonction vous pouvez les faire fonctionner, trouver la combinaison avec une autre fonction, et la liste est encore longue.
Souvent, même si vous mentionnez explicitement les fonctions, celles-ci sont sous-jacentes à l'ensemble du processus. Elles sont donc présentes, même si parfois vous ne le savez pas. Ce qui est bien, c'est que même avec des fonctions très compliquées, vous pouvez toujours représenter graphiquement une fonction pour avoir une idée de son comportement, afin d'au moins faire une éducation de ce que la fonction fait (monte, descend, etc.).




