Fonctions individuelles
Instructions : Utilisez cette calculatrice pour tester une fonction biunivoque, en montrant toutes les étapes. Veuillez taper la fonction que vous voulez vérifier dans la case ci-dessous.
Fonctions individuelles
Cette calculatrice vous permettra d'évaluer si une fonction est biunivoque ou non, en montrant toutes les étapes. La première chose à faire est d'indiquer la fonction. Il peut s'agir d'une fonction simple, linéaire ou quadratique comme "y = x^2 - 1", ou vous pouvez décider d'opter pour une fonction de type fonction rationnelle comme "f(x) = (x-1)/(x+3)".
Ensuite, lorsque vous êtes satisfait de ce que vous avez fourni et que vous vous êtes assuré que la fonction est valide, vous cliquez sur le bouton "Calculer", afin que toutes les étapes du processus vous soient présentées.
Le concept de fonction biunivoque est très important en algèbre et en calcul. Il existe de nombreuses façons simples de tester l'unicité d'une fonction, l'une d'entre elles étant la fonction Test de la ligne horizontale mais, en raison de sa nature, il est plus facile de l'utiliser pour réfuter le fait qu'une fonction est biunivoque. Pour prouver qu'une fonction est biunivoque, nous avons besoin d'un résolution d'équation , processus analytique.

Qu'est-ce qu'un processus individuel ?
En termes simples, une fonction univoque ou injective est une fonction qui, pour deux \(x_1\) et \(x_2\) différents, les valeurs de leurs images à travers \(f(x)\) sont différentes, ce qui signifie mathématiquement que
\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]Certains formateurs préfèrent l'écrire légèrement différemment, mais toujours de manière équivalente : La fonction est biunivoque si
\[\displaystyle f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \]Cela revient à dire, de manière assez sophistiquée, que si le graphique de la fonction croise la même valeur (une ligne horizontale), cela ne se produit que si le point est le même. Donc, tout ce que vous dites, c'est qu'il n'y a pas deux points différents où une ligne horizontale se croise. Vous ne faites donc que réitérer la Test de la ligne horizontale .
Comment vérifier si une fonction est univoque ou non ?
- Étape 1 : Commencez par la fonction originale f(x), et définissez l'équation y = f(x)
- Étape 2 : Tentative de résolution de x
- Étape 3 : Si vous trouvez plus d'une solution, la fonction n'est PAS biunivoque, et si elle n'a qu'une seule solution ou aucune solution, la fonction est biunivoque
Normalement, vous ferez une inspection de base pour vous assurer que cette fonction n'est manifestement pas biunivoque, peut-être parce que vous pouvez facilement trouver une ligne horizontale pour faire échouer la HLT.
Ensuite, vous rechercherez quelques propriétés visuelles de base : La fonction est-elle toujours croissante (elle est alors biunivoque), et il en va de même dans le cas où la fonction est toujours décroissante.
Quel est le lien entre l'un pour un et la recherche de l'inverse ?
En termes simples, pour trouver l'inverse d'une fonction, celle-ci DOIT être biunivoque, au moins dans un certain sous-domaine. Souvent, nous restreignons le domaine, de sorte qu'une fonction est univoque dans un domaine restreint, alors qu'elle ne le serait pas dans d'autres circonstances.
Par exemple, \(f(x) = x^2\) n'est pas globalement biunivoque. Pourquoi, parce que vous pouvez prendre deux points différents \(x_1 = -1\) et \(x_2 = 1\) et trouver que \(f(x_1) = (-1)^2 = 1\) et \(f(1) = 1^2 = 1\), ce qui signifie que la propriété (la caractérisation biunivoque)
\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]n'est pas satisfaite. Maintenant, si au lieu de considérer la ligne réelle complète \(\R\), nous ne considérons que les valeurs positives, nous pouvons conclure que la fonction est biunivoque sur les valeurs réelles positives (Indice : sur ce sous-domaine, la fonction est croissante)

Existe-t-il une formule permettant de déterminer si une fonction est biunivoque ?
Malheureusement, ce n'est pas le cas. On pourrait penser à \(\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \), comme la formule univoque, mais il s'agit plutôt d'une condition logique que d'une formule.
Cependant, il existe une procédure générique très large qui est utilisée pour tester si une fonction est biunivoque ou non, ce qui est expliqué ci-dessus. Il n'existe pas de "formule univoque". Si nous devions nous contenter d'une seule, ce serait y = f(x).
Il suffit ensuite de résoudre x. Rien de plus, rien de moins. En fin de compte, tout dépend de ce que représente f(x). Une fonction très complexe et alambiquée peut poser de nombreuses difficultés à résoudre, et vous aurez peut-être besoin d'une calculatrice de fonctions pour cela, et même avec une calculatrice de fonctions, vous pouvez échouer.
Vous vous demandez probablement pourquoi C'est parce que, au fond, nous ne disposons pas de techniques pour résoudre TOUTES les équations. Nous nous contentons de faire ce que nous pouvons avec certains types d'équations spécifiques, mais nous sommes loin de connaître une méthode EXACTE pour résoudre toutes les équations.

Exemple : fonction one-to-one
La fonction suivante est-elle injective ? \(f(x) = \frac{1}{4} x + \frac{5}{4}\)
Solution :
Nous avons reçu la fonction suivante :
\[f(x) = \frac{1}{4} x + \frac{5}{4}\]Ensuite, afin de déterminer si la fonction donnée est biunivoque ou non, nous devons résoudre \(x\) et déterminer s'il n'y a pas de solution, s'il y a une solution ou s'il y a plusieurs solutions. L'équation de départ est
\[y=\frac{1}{4}x+\frac{5}{4}\]En plaçant \(x\) du côté gauche et \(y\) et la constante du côté droit, nous obtenons
\[\displaystyle -\frac{1}{4}x = -y -\left(-\frac{5}{4}\right)\]Maintenant, en résolvant \(x\), en divisant les deux côtés de l'équation par \(-\frac{1}{4}\), on obtient ce qui suit
\[\displaystyle x=-\frac{1}{-\frac{1}{4}}y+\frac{\frac{5}{4}}{-\frac{1}{4}}\]et en simplifiant on obtient finalement ce qui suit
\[\displaystyle x=4y-5\]Par conséquent, la résolution de \(x\) pour l'équation linéaire donnée conduit à \(x=4y-5\) et il n'y a qu'une seule solution réelle, donc la fonction donnée est biunivoque.
Conclusion
Sur la base des résultats obtenus dans la section précédente, on peut conclure que la fonction donnée est biunivoque.
Graphiquement :
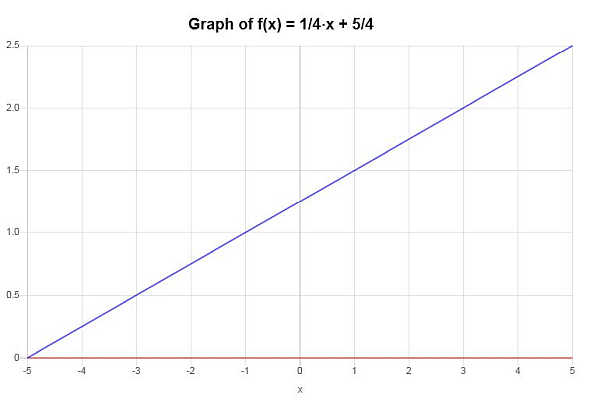
Exemple : fonction 1 pour 1
Prouvez ou réfutez que la fonction suivante est biunivoque : \(f(x) = \frac{1}{3} x^2 - 5x - \frac{5}{6}\)
Solution : Afin de déterminer si la fonction donnée est biunivoque ou non, nous devons résoudre \(x\) et déterminer s'il n'y a pas de solution, s'il y a une solution ou s'il y a plusieurs solutions. L'équation de départ que nous devons utiliser est la suivante :
\[y=\frac{1}{3}x^2-5x-\frac{5}{6}\]Étape Initiale : Dans ce cas, nous devons d'abord simplifier l'équation donnée, et pour ce faire, nous procédons aux étapes de simplification suivantes :
Les solutions sont donc les suivantes :
\[x_1=-\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \] \[x_2=\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \]Statut "one-to-one
Sur la base du travail montré ci-dessus, on peut conclure que la fonction donnée N'EST PAS UNIQUE, puisqu'elle ne passe pas le test de la ligne horizontale, car par exemple la ligne \(y = 0\) est une ligne horizontale qui traverse la fonction donnée plus d'une fois.
Graphiquement, la situation peut être décrite comme suit :
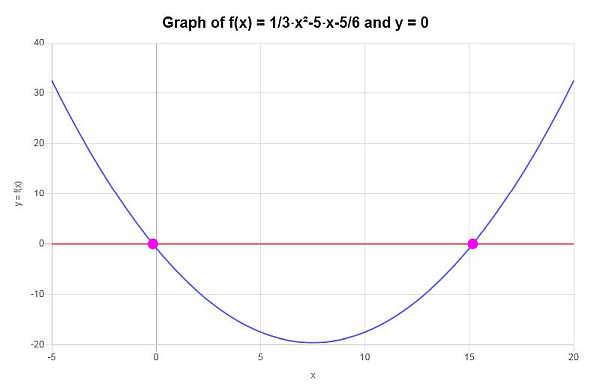
Autres calculatrices d'algèbre intéressantes
Le concept des fonctions 1 à 1 est généralement considéré comme allant de soi, mais il est très important, critique dirais-je. En effet, le concept de fonction biunivoque est étroitement lié à l'idée de fonction monotone (fonctions croissantes ou décroissantes), de même qu'il est étroitement lié à la notion d'égalité calcul de la fonction inverse et son graphique.
Pourtant, il est souvent difficile de voir la forêt derrière les arbres, car la plupart des concepts cruciaux de l'algèbre et du calcul sont étroitement liés les uns aux autres. Analyse des fonctions est l'une des choses que vous ferez tout le temps, c'est donc une bonne chose d'acquérir les compétences nécessaires pour devenir bon dans ce domaine.






