En savoir plus sur les inégalités polynomiales

Cette calculatrice peut vous aider à résoudre des inégalités polynomiales, en vous montrant toutes les étapes du processus de calcul de la solution, et en vous fournissant un graphique d'inégalité, illustrant la solution

L'inégalité que vous fournissez peut être quelque chose de simple comme "x^2 > 1", ou quelque chose de plus complexe comme "x^3 + 3x^2 + 3x + 1 > 0".

Une fois que l'inégalité polynomiale valide est fournie, veuillez cliquer sur le bouton "Calculer", afin d'obtenir la solution et toutes les étapes indiquées.

Sachez que les polynômes que vous fournissez ne se prêtent pas tous à des solutions exactes. Plus le degré du polynôme est faible, plus il est probable qu'une solution exacte à l'inégalité soit trouvée.

Qu'est-ce qu'une inégalité polynomiale ?

Une inégalité polynomiale est simplement un type d'inégalité dans laquelle les expressions impliquées sont polynomiales et dont aucun des termes n'est une expression non polynomiale. Par exemple

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \displaystyle \frac{x^3}{3} \]

est une inégalité polynomiale, alors que

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \sin(x) \]

est un non, à cause de la présence du terme \(\sin x\), qui n'est pas un polynôme. Résolution d'inéquations en général est un processus difficile, mais pour les polynômes, nous avons un plan d'action clair.

Comment résoudre une inégalité polynomiale ?

• Étape 1 : Assurez-vous que tous les termes sont des polynômes. Si ce n'est pas le cas, les méthodes spécifiques utilisées pour les polynômes peuvent ne pas s'appliquer
• Étape 2 : Mettez tout d'un côté, en laissant zéro de l'autre côté
• Étape 3 : En remplaçant le signe d'inégalité par "=", résolvez l'équation associée (il s'agit de trouver les zéros d'un polynôme)
• Étape 4 : Recueillir tous les points critiques de l'inégalité, qui dans ce cas sont les zéros réels de l'auxiliaire Equation polynomiale (on ne considère pas les racines complexes dans ce cas)
• Étape 5 : S'il n'existe aucun point critique, cela signifie que l'expression ne change pas de signe, et donc que toute la ligne réelle sera une solution, ou bien qu'il n'y a pas de solution. Pour vérifier, choisissez un point quelconque et voyez s'il satisfait à l'inégalité. Si c'est le cas, toute la droite réelle est la solution, sinon, il n'y a pas de solution
• Étape 6 : S'il y a des points critiques, construisez des intervalles avec des points critiques consécutifs (en utilisant -∞ comme point critique de départ et ∞ comme point critique d'arrivée)
• Étape 7 : Vérifiez chacun de ces intervalles et voyez si un point situé à l'intérieur satisfait à l'inégalité. Si c'est le cas, l'intervalle fait partie de la solution, sinon, l'intervalle ne fait pas partie de la solution.

L'idée clé ici est que les points critiques et les intervalles qui en découlent sont des intervalles pour lesquels l'expression ne change pas de signe, de sorte que soit l'intervalle entier est une solution, soit aucun point de l'intervalle ne fait partie de la solution.

Zéros polynomiaux et points critiques

L'une des raisons pour lesquelles il est possible de résoudre des inéquations polynomiales est qu'il est relativement simple d'analyser les expressions polynomiales à la recherche de points critiques, outre le fait que les polynômes sont des expressions continues.

Il y aura des inégalités telles que

\[\displaystyle \frac{\sin(x^2-1)}{x^3-1} < 1 \]

où il sera beaucoup plus difficile de trouver les points critiques. inégalités linéaires sont encore plus simples pour trouver les points critiques, mais c'est à peu près tout. Toute inégalité générale présente ses propres complexités.

Applications des polynômes dans la vie réelle

Il existe de nombreuses applications des polynômes. Par exemple, en physique, lorsque vous étudiez la cinématique, il existe des expressions polynomiales intéressantes dérivées des lois de Newton. Ces expressions peuvent définir des conditions pour la position d'un corps, ce qui peut conduire à une inégalité polynomiale pour déterminer à quel moment le corps est au-dessus d'une certaine hauteur, ce qui peut s'avérer crucial en balistique, par exemple.

De même, lorsque vous étudiez les équations différentielles, vous pouvez trouver dans l'équation des termes qui dépendent d'une puissance et ont une structure polynomiale, pour lesquels vous pouvez utiliser des inégalités avancées, telles que les inégalités de Gronwall.

Exemple : résolution d'inégalités polynomiales

Résoudre : \(x^2 - x > \frac{1}{2}\)

Solution : Nous devons d'abord résoudre l'équation quadratique suivante \(\displaystyle x^2-x-\frac{1}{2}=0\) :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(1\right)\left(-\frac{1}{2}\right)}}{2\cdot 1} = \displaystyle \frac{1 \pm \sqrt{3}}{2}\]

donc, nous trouvons que :

\[ {x}_1 = \frac{1}{2}-\frac{1}{2}\sqrt{3}=-\frac{1}{2}\sqrt{3}+\frac{1}{2} \] \[{x}_2 = \frac{1}{2}+\frac{1}{2}\sqrt{3}=\frac{1}{2}\sqrt{3}+\frac{1}{2}\]

Analyse des points critiques

La liste des points critiques trouvés, classés par ordre croissant, est la suivante : \(-\frac{1}{2}\sqrt{3}+\frac{1}{2}\), \(\frac{1}{2}\sqrt{3}+\frac{1}{2}\).

Sur cette base, nous devons analyser les intervalles suivants :

- Pour l'intervalle \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) : Le côté gauche est positif, donc \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) fait partie de la solution.

- Pour l'intervalle \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) : Le côté gauche est négatif, ce qui signifie que \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) ne fait pas partie de la solution.

- Pour l'intervalle \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\) : Le côté gauche est positif, ce qui signifie que \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\) fait partie de la solution.

Solution à l'inégalité

En se basant sur l'inégalité fournie et en analysant les points critiques, on trouve que la solution de l'inégalité est : \(x < -\frac{1}{2}\sqrt{3}+\frac{1}{2}\) ou \(x > \frac{1}{2}\sqrt{3}+\frac{1}{2}\).

En utilisant la notation par intervalles, la solution s'écrit comme suit :

\[\left(-\infty,-\frac{1}{2}\sqrt{3}+\frac{1}{2}\right) \cup \left(\frac{1}{2}\sqrt{3}+\frac{1}{2},\infty\right)\]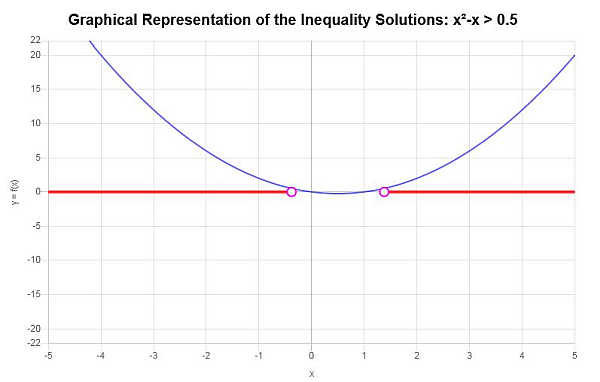

qui conclut le calcul.

Exemple : polynôme de degré supérieur

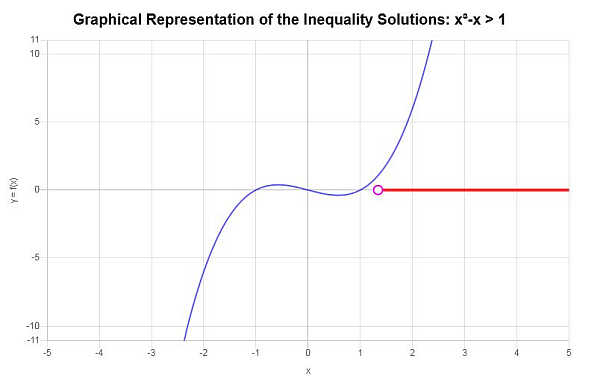
Résolvez l'inégalité suivante : \(x^3 - x > 1\)

Solution :

Pour résoudre \(x^3-x > 1\), il faut d'abord tout mettre de côté :

\[x^3-x-1> 0\]

A partir de là, nous obtenons l'équation associée qui doit être résolue en premier, qui est \(x^3-x-1=0\). Observez que le degré est \(\displaystyle deg(p) = 3\), son coefficient directeur est \(\displaystyle a_{3} = 1\) et son coefficient constant est \(\displaystyle a_0 = -1\).

Tentative de racines rationnelles

Nous allons d'abord essayer de trouver des racines rationnelles simples, avec le théorème du zéro rationnel.

La tâche suivante consiste à trouver les nombres entiers qui divisent le coefficient principal \(a_{3}\) et le coefficient constant \(a_0\), qui seront utilisés pour construire nos candidats aux zéros de l'équation polynomiale.

les diviseurs de \(a_{3} = 1\) sont : \(\pm 1\).

les diviseurs de \(a_0 = -1\) sont : \(\pm 1\).

Par conséquent, en divisant chaque diviseur du coefficient constant \(a_0 = -1\) par chaque diviseur du coefficient directeur \(a_{3} = 1\), nous trouvons la liste suivante de candidats à être des racines :

\[\pm \frac{ 1}{ 1}\]

Maintenant, tous les candidats doivent être testés pour voir s'ils constituent une solution. Les résultats suivants sont obtenus en testant chaque candidat :

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -1^3-\left(-1\right)-1 & = & \displaystyle -1 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 1^3-1-1 & = & \displaystyle -1 \ne 0 \\\\ \end{array}\]

Mais comme nous n'avons pas trouvé de racines rationnelles par inspection, nous ne pouvons pas poursuivre la factorisation en utilisant des méthodes élémentaires, et le processus s'arrête donc ici.

OPTIONNEL : Il s'agit d'un polynôme de degré \(3\), pour lequel il existe un total de \(3\) racines, même si certaines peuvent être complexes, mais dans ce cas moins de \(3\) solutions ont été trouvées en utilisant des méthodes élémentaires.

En utilisant des méthodes avancées d'équation cubique, on peut trouver que l'ensemble complet des solutions est :

\[x_1=\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\]
\[x_2=\frac{\frac{1}{6}\cdot \left(-3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}+i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]
\[x_3=\frac{\frac{1}{6}\cdot \left(3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]

Analyse des points critiques

Le seul point critique trouvé est \(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\).

Sur cette base, nous devons analyser les intervalles suivants :

- Pour l'intervalle \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\) : Le côté gauche est négatif, donc \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\) ne fait pas partie de la solution.

- Pour l'intervalle \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\) : Le côté gauche est positif, ce qui implique que \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\) fait partie de la solution.

Solution à l'inégalité

En se basant sur l'inégalité fournie et en analysant les points critiques, on trouve que la solution de l'inégalité est : \(x > 1.3247180451128\).

En utilisant la notation par intervalles, la solution s'écrit comme suit :

\[\left(1.3247180451128,\infty\right)\]

Graphiquement :

Plus de calculateurs d'inégalité

Résolution d'inéquations (interdit de recherche de solutions à des équations ) est l'une des opérations les plus courantes en mathématiques.

La résolution des inégalités est souvent laborieuse et il n'existe généralement pas de règle pour les résoudre. Résolution d'inéquations polynomiales est l'une des rares exceptions, dans laquelle nous pouvons suivre une série d'étapes pour trouver les solutions, mais nous pouvons quand même échouer, car les polynômes de degré supérieur sont difficiles à traiter. En effet, il est vraiment impossible de trouver les racines des polynômes au-dessus du degré 5 en utilisant une règle générale (théorème d'Abel).