À propos de la règle de chaîne

Cette calculatrice vous permettra d'appliquer la règle de la chaîne à toute fonction composite que vous fournissez. UN Fonction composite correspond au cas où vous évaluez une fonction à l'intérieur d'une fonction. Pour que le calculateur de règle de chaîne fonctionne, vous devez fournir une fonction composite valide et différentiable.

Un exemple de fonction valide serait f(x) = (sin(x))^2, où nous avons ici la fonction 'x^2' qui est évaluée à une autre fonction, qui est sin(x), formant un fonction composée.

Une fois qu'une fonction valide et différentiable a été fournie, la prochaine chose que vous devez faire est de cliquer sur le bouton qui lit "Calculer", ce qui déclenchera alors les calculs et vous montrera toutes les étapes.

La dérivée de la règle de la chaîne est l'une des règles de différenciation les plus couramment utilisées. En effet, la composition de fonctions est l'un des moyens les plus naturels de construire de nouvelles fonctions basées sur des fonctions élémentaires.

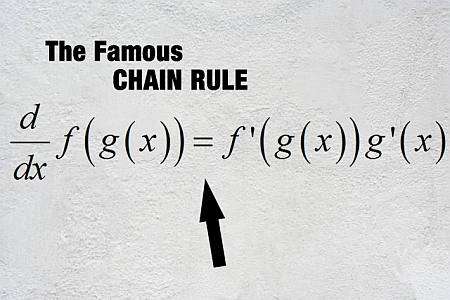
Quelle est la règle de la chaîne

En termes simples, la règle de chaîne permet de différencier les fonctions composites, c'est-à-dire les fonctions qui sont évaluées à l'intérieur d'autres fonctions. Donc, disons que nous avons la fonction \(f(x)\) et \(g(x)\), et nous savons comment calculer la dérivée de ces fonctions, qui sont \(f'(x)\) et \(g'(x)\).

Ensuite, il y a un Formule de règle de chaîne qui nous permet de calculer la dérivée de la fonction composée \(f \circ g\), qui est définie comme \((f \circ g)(x) = f(g(x))\) :

\[\displaystyle (f \circ g)'(x) = f'(g(x))g'(x)\]

Étapes d'utilisation de la règle de chaîne

• Étape 1: Identifier la fonction externe f(x) et la fonction interne g(x)
• Étape 2: Assurez-vous que f(x) et g(x) sont des fonctions valides et différentiables, et calculez les dérivées correspondantes f'(x) et g'(x)
• Étape 3: Utilisez la formule (f \circ g)'(x) = f'(g(x))g'(x), qui indique que nous évaluons la dérivée de la fonction externe à la fonction interne, et multiplions cela par la dérivée de la fonction interne

Observez comment les étapes ci-dessus utilisent l'idée de fonction « interne » et « externe ». Ce n'est peut-être pas un terme standard, mais plutôt une idée qui peut vous aider à identifier le rôle joué par chaque fonction lors de l'utilisation de la règle de chaîne.

Applications de règle de chaîne

La règle de la chaîne est en effet un excellent outil pour trouver des dérivés, et normalement la clé de tout calculatrice dérivée , ainsi que tous les autres éléments de base Règles relatives aux produits dérivés . Mais la règle de la chaîne a une interprétation particulière dans ce qu'on appelle Tarifs Associés

Pour donner un contexte à l'idée de taux liés, commençons par une forme d'écriture de la règle de la chaîne que beaucoup de gens trouveront peut-être plus facile à comprendre :

\[\displaystyle \frac{dy}{dx} = \displaystyle \frac{dy}{dz} \cdot \frac{dz}{dx} \]

La forme ci-dessus de la règle de chaîne dit que si vous \(y\) est une fonction de \(z\) et \(z\) est une fonction de \(x\), alors \(y\) est finalement une fonction de \(x\), et vous pouvez trouver la dérivée de \(y\) par rapport à \(x\) en utilisant la règle de chaîne.

Comme vous vous en doutez probablement, \(y\) joue le rôle de \(f(x)\) (la fonction 'externe') et \(z\) joue le rôle de \(g(x)\) (la fonction 'interne').

La forme ci-dessus de la règle de la chaîne relie le taux de variation de y par rapport à x, avec les taux de variation de y par rapport à z et celui de z par rapport à x, d'où le terme « taux liés ».

Ceci est extrêmement utile dans la pratique. Exemple : le rayon d'un cercle augmente à une vitesse de 2 cm/sec, quelle est la vitesse de variation de l'aire du cercle ? Ainsi, vous pouvez soit aller exprimer le rayon du cercle en fonction de t, reflétant le fait qu'il augmente à un taux de 2 cm/sec, OU, vous pouvez utiliser la règle de la chaîne.

Vous appelez donc A l'aire, r le rayon et t le temps. Ce que vous devez calculer est \(\displaystyle \frac{dA}{dt}\), donc vous utilisez directement la règle de la chaîne, puisque vous savez \(A = \pi r^2\), et r'(t) = 2, donc alors

\[\displaystyle \frac{dA}{dt} = \displaystyle \frac{dA}{dr} \cdot \frac{dr}{dt} = 2\pi r \cdot 2 = 4 \pi r \]

Règle de chaîne dérivée partielle

Pouvez-vous utiliser la règle de chaîne avec dérivés partiels ? Bien sûr, la différenciation partielle est comme la différenciation régulière, sauf que les autres variables sont supposées constantes, alors l'habituel Règles relatives aux produits dérivés appliquer.

Alors, l'idéal de la règle de la chaîne multivariable s'applique, seule cette variable varie à la fois.

Intégration de la règle de chaîne

La règle de la chaîne dans le sens où elle ne s'applique pas comme un outil dérivé, mais devient plutôt un outil d'intégration inestimable pour les substitutions et les changements de variables.

Il peut être conçu comme une sorte de règle de chaîne inversée.

Exemple : utilisation de la règle de chaîne

Calculer la dérivée de la fonction : \(f(x) = \sin(\cos(x)) \)

Solution: Considérons la fonction \(\displaystyle f(x)=\sin\left(\cos\left(x\right)\right)\). Cette fonction correspond à la composition de deux fonctions : sin(x) et cos(x), raison pour laquelle la Chain Rule s'appliquerait dans ce cas.

Quelle est la conclusion : Nous pouvons conclure que la dérivée que nous recherchons est :

\[f'(x) = -\cos\left(\cos\left(x\right)\right)\sin\left(x\right)\]

et ceci conclut le calcul.

Exemple de règle de chaîne

À l'aide de la règle de chaîne et de toute autre règle dérivée, calculez : \(\displaystyle \frac{d}{dx} \left( \cos(x^2) \right)^2\)

Solution: Dans cet exemple, nous avons la fonction \(\displaystyle f(x)=\cos\left(x^2\right)\), qui correspond à une fonction composée, qui indique que la règle de chaîne est la bonne règle dérivée pour commencer (d'autres règles seront nécessaires au cours des calculs)

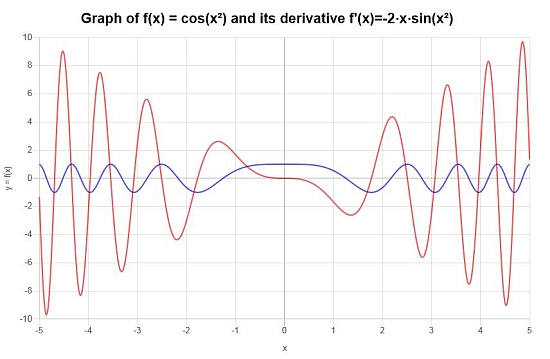
Dérivé Final : La conclusion est que la dérivée de la fonction fournie est donnée par :

\[f'(x) = -2x\sin\left(x^2\right)\]

On peut construire la représentation graphique suivante sur l'intervalle \([-5, 5]\) :

Exemple : autre calcul de règle de chaîne

Calculez la dérivée de \( f(x) = x^2 \sin(x^2)\) en utilisant la règle de chaîne.

Solution:

On a fourni la fonction suivante : \(\displaystyle f(x)=x^2\sin\left(x^2\right)\), pour laquelle nous devons calculer sa dérivée.

La fonction est déjà simplifiée, nous pouvons donc procéder directement au calcul de sa dérivée :

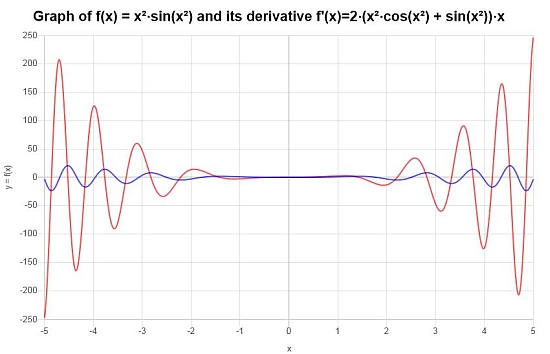
Quelle est la conclusion finale : La conclusion finale est que la dérivée recherchée est donnée par :

\[f'(x) = 2\left(x^2\cos\left(x^2\right)+\sin\left(x^2\right)\right)x\]

Graphiquement nous avons :

Autres calculatrices dérivées

certainement à l'aide d'un calculatrice de dérivées facilitera les choses lorsqu'il s'agit de fonctions assez compliquées. Le processus de différenciation devient important grâce à l'utilisation d'éléments communs, faciles à retenir. Règles relatives aux produits dérivés y compris le Règle Du Produit , la Quotient Rule et le Règle De La Chaîne .

Ces règles vous aideront à traiter chaque fonction différentiable, mais le processus algébrique du calcul et simplification n'est pas nécessairement facile.