En savoir plus sur cette calculatrice de sommets

Cette calculatrice vous permet d'obtenir une fonction quadratique que vous fournissez en Forme du vertex en montrant toutes les étapes. Vous devez fournir une expression quadratique valide en x. Toute fonction quadratique valide fonctionnera.

Par exemple, vous pouvez fournir quelque chose comme x^2 + 3x + 4, ou peut-être que vous pouvez fournir une expression qui n'est pas simplifiée, comme x^2 + 3x - 1/2 x + 3x^2 - 3.

Une fois que vous avez fourni une fonction quadratique valide, il vous suffit de cliquer sur "Calculer" et le calcul de la forme du sommet vous sera présenté, avec toutes les étapes fournies par ce programme Calculatrice de paraboles .

Toute fonction quadratique valablement définie aura une forme de sommet, à partir de laquelle il sera direct d'obtenir les coordonnées du sommet, et de savoir si la parabole s'ouvre "vers le haut" ou "vers le bas".

Comment trouver la forme du sommet d'une parabole ?

Toutes les fonctions quadratiques sont représentées graphiquement par une parabole. Cette parabole s'ouvrira vers le haut ou vers le bas, selon le signe du coefficient directeur.

En fin de compte, pour obtenir la parabole sous la forme d'un sommet, il faut trouver le sommet de la fonction quadratique, ce qui s'effectue comme suit Compléter le carré .

Quelles sont les étapes du calcul de la forme du sommet ?

Alors, comment trouver la forme du sommet ? Vous pouvez suivre les étapes suivantes :

• Étape 1 : Identifiez la fonction quadratique. L'expression doit être de degré 2, et le premier coefficient multiplicateur de x² doit être différent de zéro
• Étape 2 : Si le coefficient directeur qui multiplie x² est positif, la parabole s'ouvre vers le haut, et s'il est négatif, elle s'ouvre vers le bas
• Étape 3 : Complétez les carrés, et remarquez le terme à l'intérieur des parenthèses avec x, car il détermine la coordonnée x du sommet
• Étape 4 : Après avoir complété les carrés, la constante à l'extérieur de la parenthèse (elle peut être nulle) correspond à la coordonnée y du sommet

Par conséquent, nous pouvons voir que le processus général de calcul de la forme du sommet est étroitement lié au processus d'achèvement des carrés.

Existe-t-il une formule des sommets ?

En fait, oui. Normalement, l'achèvement du processus des places est la meilleure façon de procéder. Supposons que vous ayez un fonction quadratique exprimée par :

\[ f(x) = a x^2 + b x + c\]

Vous avez donc déjà une fonction quadratique simplifiée. La coordonnée x du sommet est calculée à l'aide de la formule suivante :

\[ x_v = \displaystyle \frac{-b}{2a} \]

C'est très simple, n'est-ce pas ? Oui. Mais alors, comment obtenir la coordonnée y du sommet ? On prend la valeur \(x_v\) et on l'introduit dans la fonction quadratique. Nous obtenons donc

\[ y_v = f(x_v) = a x_v^2 + b x_v + c \]

Naturellement, cette formule peut être beaucoup plus rapide que la méthode consistant à compléter les carrés, mais chaque méthode a son utilité, et les circonstances d'un problème donné vous indiqueront la forme à utiliser. .

Forme quadratique à sommet ?

Pourquoi vouloir passer de la forme quadratique à la forme sommet ? Il y a plusieurs raisons : d'un point de vue géométrique, la forme sommet permet de voir la fonction quadratique donnée comme une translation et un changement d'échelle d'une parabole élémentaire, où la translation est déterminée par le sommet, et l'échelle est déterminée par le coefficient directeur.

Le calcul peut demander beaucoup de travail, mais cette Calculatrice de paraboles fera le travail fastidieux pour vous.

Forme standard ou forme de sommet ?

Il y a généralement une certaine confusion à ce sujet. Permettez-moi de préciser que la forme du sommet est un autre nom donné à la forme standard. Ainsi, la forme standard d'une fonction quadratique \(y = a(x-h)^2 + k\) est la même que la forme du sommet.

La confusion vient du fait que les gens utilisent parfois la forme générale d'une quadratique lorsqu'ils se réfèrent à la forme standard. La forme générale est \(y = ax^2 + bx + c\).

La question qui se pose est donc de savoir comment passer de la forme générale à la forme des sommets, ce qui revient à demander comment passer de la forme générale à la forme standard. La réponse est simple : Commencez par la forme générale et ensuite vous Compléter les carrés pour obtenir la forme standard.

Exemple : comment trouver la forme du sommet

Trouvez le sommet de l'expression quadratique suivante \(f(x) = x^2 + 3x - 6\) en utilisant la formule du sommet

Solution : Nous devons trouver la forme du sommet de la fonction quadratique \(\displaystyle f(x)=x^2+3x-6\).

Nous commençons par calculer les coordonnées du sommet de la parabole associée à la fonction quadratique donnée.

Pour une fonction quadratique de la forme \(f(x) = a x^2 + bx + c\), la coordonnée x du sommet est calculée à l'aide de la formule suivante :

\[x_V = \displaystyle -\frac{b}{2a}\]

Dans ce cas, nous savons que la fonction dont nous devons trouver le sommet est \(f(x) = \displaystyle x^2+3x-6\), ce qui implique que les coefficients correspondants sont :

\[a = 1\] \[b = 3\] \[c = -6\]

En introduisant les valeurs connues de \(a\) et \(b\) dans la formule de la coordonnée x du sommet, on obtient :

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 1} = -\frac{3}{2}\]

Il faut maintenant introduire la valeur de \(x_V = \displaystyle -\frac{3}{2}\) dans la fonction quadratique :

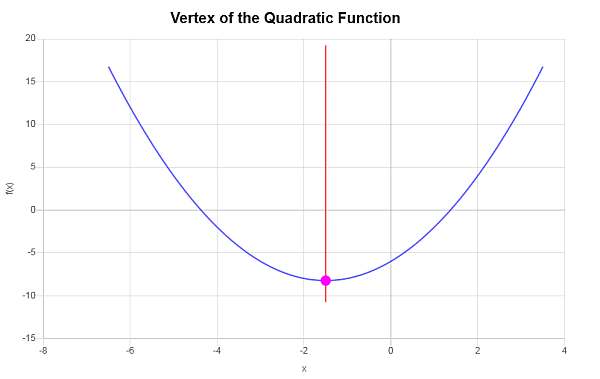
\[y_V = f(x_V)\] \[ = 1\cdot \left(-\frac{3}{2}\right)^2+3\cdot \left(-\frac{3}{2}\right)-6=1\cdot\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}-\frac{9}{2}-6=-\frac{33}{4}\]

Par conséquent, la coordonnée x du sommet est \(x_V = \displaystyle -\frac{3}{2}\), et la coordonnée y du sommet est \(y_V = \displaystyle -\frac{33}{4}\). Cela indique que le point qui représente le sommet est \( \displaystyle \left(-\frac{3}{2}, -\frac{33}{4}\right)\).

Le résultat suivant est obtenu graphiquement :

Nous devons compléter le carré de l'expression quadratique \(\displaystyle x^2+6x-2\).

Les étapes suivantes doivent être suivies pour compléter le carré :

Étape 1 : Dans ce cas, puisque la constante de tête, le terme qui multiplie \(x^2\) dans le polynôme donné, est \(a = 1\), nous n'avons pas à la factoriser.

Étape 2 : Nous forçons un '2' devant le terme \(x\) en observant que le terme d'ordre 1 dans l'expression quadratique donnée peut être réécrit : \(\displaystyle 6 x = 2 \cdot \left(3\right) x\), ce qui nous donne \[ x^2+6x-2 = x^2+2 \cdot \left(3\right) x-2 \]

Étape 3 : Le terme qui multiplie 2 dans ce cas est \(\displaystyle 3\), donc pour utiliser l'équation binomiale, il faut que son carré \(\displaystyle \left(3\right)^2\) soit dans l'expression.

Pour ce faire, nous ajoutons et soustrayons le terme \(\displaystyle \left(3\right)^2 = 9\), afin de compléter le carré. Ajouter et soustraire le même terme revient à ajouter zéro, ce qui n'affecte donc pas l'expression : \[ \begin{array}{ccl} \displaystyle x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \end{array}\]

Étape 4 : Nous complétons le carré et simplifions les constantes : \[ \begin{array}{ccl} x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x+9-2-9 \\\\ \\\\ & = & \displaystyle \left[x^2+2 \cdot \left(3\right) x+\left(3\right)^2\right]-2-9 \\\\ \\\\ & = & \displaystyle \left( x+3 \right)^2-11 \end{array}\]

Conclusion : Par conséquent, nous constatons que la fonction sous forme de sommet est \(\displaystyle f(x) = \left( x+3 \right)^2-11\), ce qui complète le calcul.

Exemple : forme quadratique à sommet

Convertissez la forme quadratique suivante \(f(x) = x^2 + 6x - 2\) en forme de sommet. Quelles sont les coordonnées du sommet ? La parabole s'ouvre-t-elle vers le haut ou vers le bas ?

Solution :

Nous devons trouver la forme du sommet de la fonction quadratique \(\displaystyle f(x)=x^2+6x-2\).

Nous commençons par calculer les coordonnées du sommet de la parabole associée à la fonction quadratique donnée.

Pour une fonction quadratique de la forme \(f(x) = a x^2 + bx + c\), la coordonnée x du sommet est calculée à l'aide de la formule suivante :

\[x_V = \displaystyle -\frac{b}{2a}\]

Dans ce cas, nous savons que la fonction dont nous devons trouver le sommet est \(f(x) = \displaystyle x^2+6x-2\), ce qui implique que les coefficients correspondants sont :

\[a = 1\] \[b = 6\] \[c = -2\]

En introduisant les valeurs connues de \(a\) et \(b\) dans la formule de la coordonnée x du sommet, on obtient :

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{6}{2 \cdot 1} = -3\]

Il faut maintenant introduire la valeur de \(x_V = \displaystyle -3\) dans la fonction quadratique :

\[y_V = f(x_V)\] \[ = 1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=-3^2+6\cdot \left(-3\right)-2=9-18-2=-11\]

Par conséquent, la coordonnée x du sommet est \(x_V = \displaystyle -3\), et la coordonnée y du sommet est \(y_V = \displaystyle -11\). Cela indique que le point qui représente le sommet est \( \displaystyle \left(-3, -11\right)\).

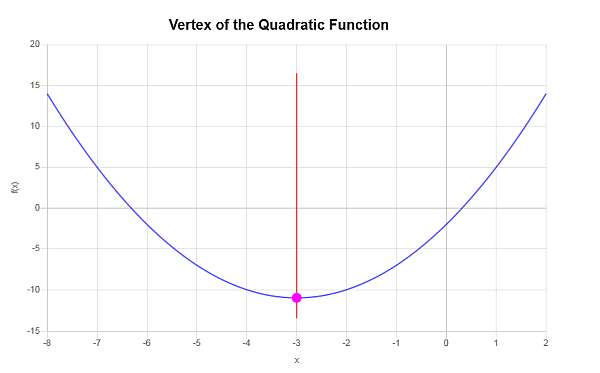
Nous devons compléter le carré de l'expression quadratique \(\displaystyle x^2+6x-2\).

Les étapes suivantes doivent être suivies pour compléter le carré :

Étape 1 : Dans ce cas, puisque la constante de tête, le terme qui multiplie \(x^2\) dans le polynôme donné, est \(a = 1\), nous n'avons pas à la factoriser.

Étape 2 : Nous forçons un '2' devant le terme \(x\) en observant que le terme d'ordre 1 dans l'expression quadratique donnée peut être réécrit : \(\displaystyle 6 x = 2 \cdot \left(3\right) x\), ce qui nous donne \[ x^2+6x-2 = x^2+2 \cdot \left(3\right) x-2 \]

Étape 3 : Le terme qui multiplie 2 dans ce cas est \(\displaystyle 3\), donc pour utiliser l'équation binomiale, il faut que son carré \(\displaystyle \left(3\right)^2\) soit dans l'expression.

Pour ce faire, nous ajoutons et soustrayons le terme \(\displaystyle \left(3\right)^2 = 9\), afin de compléter le carré. Ajouter et soustraire le même terme revient à ajouter zéro, ce qui n'affecte donc pas l'expression : \[ \begin{array}{ccl} \displaystyle x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \end{array}\]

Étape 4 : Nous complétons le carré et simplifions les constantes : \[ \begin{array}{ccl} x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x+9-2-9 \\\\ \\\\ & = & \displaystyle \left[x^2+2 \cdot \left(3\right) x+\left(3\right)^2\right]-2-9 \\\\ \\\\ & = & \displaystyle \left( x+3 \right)^2-11 \end{array}\]

Conclusion : Par conséquent, nous constatons que la fonction sous forme de sommet est \(\displaystyle f(x) = \left( x+3 \right)^2-11\), ce qui complète le calcul.

Autres calculatrices quadratiques

La plupart des calculatrices quadratiques reposent d'une manière ou d'une autre sur le processus de Compléter les carrés qui permet de regrouper les éléments entre parenthèses qui sont élevés au carré.

Comme nous pouvons le voir dans la formule du sommet, le calcul du sommet est étroitement lié au formule quadratique et le calcul des racines de l'équation quadratique . .